Symmetric crypto AES

In modern cryptography exist the concept of symmetric and asymmetric cryptography. Symmetric cryptography means that you use the same key for encryption and decryption. In asymmetric cryptography you have two keys, one is for encryption, known as the public key, and the other one is for decryption, known as the private key.

A commonly used algorithm today for symmetric cryptography is AES, which means "Advanced Encryption Standard".

1 AES (Symmetric crypto)

This algorithm has a combination of substitutions and transpositions using a key of fixed length. A key of fixed length means that the algorithm can only have a key with a certain size. However, AES has different versions, and each version can support a key length of different sizes. The most common versions are AES 128 and AES 256, which have a key length of 128 bits and AES 256 respectively. The AES algorithm is considered secure. However, the implementation can be attacked successfully if it has flaws. For example, one famous way to break AES encryption is the Padding Oracle Attack, which allows one to successfully crack SSL, an encrypted protocol that was widely used to secure HTTP traffic. However, this is not a weakness of AES, but a weakness in how it is used.
AES has different operation modes. We will analyze two of them to illustrate vulnerabilities that can emerge in their use. These operation modes are "ECB" and "CBC".

1.1 AES operation mode ECB

ECB means Electronic Code Book. In this operation mode, we encrypt independently blocks of the clear text according to the key length. For example, if we are using AES 128, we break the clear text into chunks of 128 bits and use AES to encrypt them independently. This causes a problem because it leaks structure in the encrypted text. There is a famous example on the internet about an image of Tux (the penguin from Linux) encrypted using AES in ECB operation mode:

Encrypted image using AES on ECB mode:

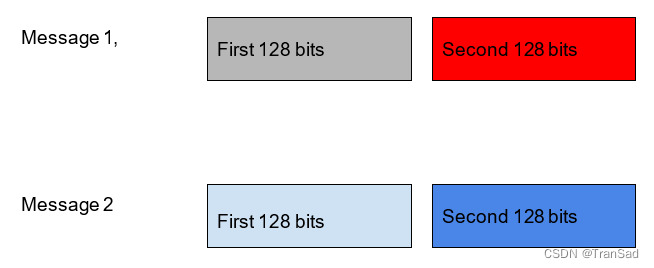
You can see that is easy to identify that the encrypted image contains the penguin. In other cases, this operation mode can be very bad for other reasons. Suppose you are sending an encrypted text and you know that the first 128 bits contain a name, and the second 128 bits contain a date. Imagine that you are an attacker that captures some encrypted messages on different dates. Even if you do not know the key, you could be able to interchange the second block of messages to tamper with the date. To understand this better let’s look at an example. Suppose you intercept a message sent on May 1, and after some days you intercept another message on May 8.

Imagine you want to make the receiver think that the second message is from May 1. You could simply replace the blue block with the red block.

Another problem of ECB is that if you send the same message twice, any attacker can see that the same message is being sent again. A secure encryption algorithm should not leak any information about the message. Knowing that the same message was sent in the past can be used to learn details about the communication. It is recommended to never use ECB.

1.2 AES operation mode CBC

A more secure operation mode is CBC, which means Cipher Block Chaining. In this mode, we include additional elements. The first one is the initialization vector, a random value with the same size as the key. In AES, the key size is the same as the block size. Remember that in AES we must separate the cleartext into blocks with the same size as the key. Before starting the encryption, we do XOR between the first block of cleartext and the Initialization Vector, then we begin to encrypt using AES with the key of our choice. The initialization vector is different for every message, so if we send the same message twice, it will be different due to the initialization vector. We must attach the initialization vector to the message. Another element we add in this operation mode is that we do not encrypt blocks independently, but we use the encrypted text from one block and XOR it with the next block of cleartext we want to encrypt. Then, we use AES and the key to encrypt that result. In the following image it is shown the graphical representation of what was just explained, note that the circle with the cross means XOR:

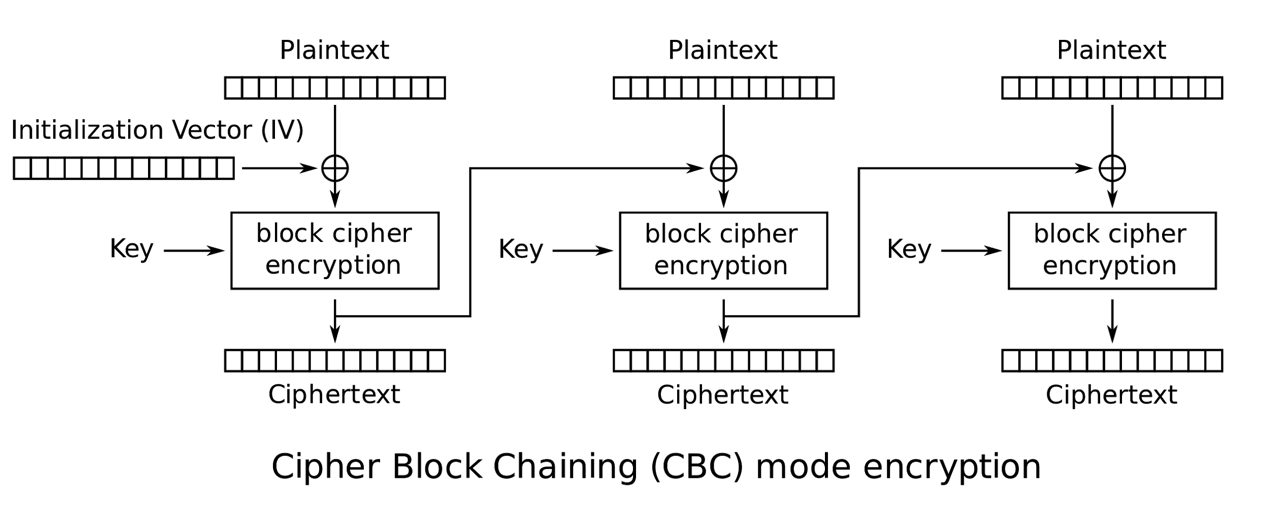
In AES, the cleartext must be the same size as a multiple of the block size. For example, if you have a cleartext that happens to be shorter than a block, you need to add padding to the cleartext, so it matches at least one block. In a case where the cleartext is larger than one block but smaller than two, you need to add padding to the cleartext until it is the same size as two blocks. In AES there is a common way of padding, which is a standard called PKCS #7. In AES 128, as we said previously, the block size is 128 bits, which is equivalent to 16 bytes. Suppose you want to encrypt the message

"HELLOPICOCTF"

Since that message is 12 bytes, we require to add a padding of 4 bytes to complete the size of a block. In PKCS#7 you add padding using a byte with the value of bytes you need to pad. In our example, since we need to pad 4 bytes to complete 16 bytes, we would pad like this:

"HELLOPICOCTF"+"\x04\x04\x04\x04"

Note that "\x" is a way to tell that in a string we want to use that exact number on a byte, even if it is not printable ASCII. Now, suppose we want to encrypt a message of 15 bytes like:

"GOODBYEPICOCTF!"

After we pad it using PKCS#7, the result is:

"GOODBYEPICOCTF!"+"\x01"

What would be the result after padding the message "BYEPICOCTF"?

…

If you answered:

"BYEPICOCTF"+"\x06\x06\x06\x06\x06\x06"

You are correct.