用二叉树或栈求表达式的值--代码实现+算法分析

文章目录

1. 利用栈解决表达式求值问题
- 1.2 根据表达式求后缀表达式
2. 二叉树求表达式值

解决表达式求值问题有两种方法，一种是利用栈和后缀表达式求解，另一种是二叉树中序存储表达式。所以本文分为栈和二叉树两大部分带领读者求解表达式。

1. 利用栈解决表达式求值问题

所谓表达式，就是由变量、常量以及运算符组合而成的式子。其中，常用的运算符无非 !（阶乘运算符）、^（指数运算符）、+、-、*、/ 、( ) 这几种，比如 3!+4*2/(1-5)^2 就是一个表达式。那么，如何用求一个表达式的值呢。用后缀表达式法。

什么是后缀表达式？就是将表达式中所有运算符放在它的运算项后面

这里以 3!+4*2/(1-5)^2 为例：6+8/16

! 运算符对应的运算项为 3，转换后得到3!
+运算符对应的运算项是 3! 和 4*2/(1-5)^2，转换之后得到：3! 4*2/(1-5)^2 +
*运算符对应的运算项是 4 和 2，转换之后得到 4 2 *
/ 运算符对应的运算项是4 2 *和(1-5)^2，转换后得到 4 2 * (1-5)^2 /
-运算符对应的运算项是 1 和 5，转换后得到1 5 -
^运算符对应的运算项是1 5 -和2，转换后得到 1 5 - 2 ^。

整合之后，整个普通表达式就转换成了 3 ! 4 2 * 1 5 - 2 ^ / +这就是其对应的后缀表达式。

得到的后缀表达式，如何计算？首先创建一个栈。接着按照从左到右的顺序扫描后缀表达式，遇到运算项就入栈。遇到n元运算符，就出栈顶元素n个计算并将计算结果压回栈中。代码实现应注意的是：从栈出来的先后顺序，对应原来运算的哪一个运算项！

如：遇到阶乘（一元运算符），出栈顶计算。遇到乘法（二元运算符），出栈顶两元素计算并压回栈中。循环上述操作，最后栈中最后一个元素，即为此运算项即为整个表达式的值。

根据后缀表达式求值代码实现

double calculate(char* out)
{
	int index = 0;
	stack<double>result;
	while (out[index] != '\0')
	{
		char c = out[index];
		switch (c)
		{
			case '!':
			{
				double i = result.top();
				result.pop();
				double end = 1;
				while (i != 1) end *= i-- ;
				result.push(end);
				break;
			}
			case '*':
			{
				double right = result.top();
				result.pop();
				double left = result.top();
				result.pop();
				result.push(left * right);
				break;
			}
			case '/':
			{
				double right = result.top();//被除数
				result.pop();
				double left = result.top();//除数
				result.pop();
				if (!right)
				{
					cout << "分母为零，错误" << endl;
					exit(-1);
				}
				else
				{
					result.push(left / right);
					break;
				}
			}
			case '+':
			{
				double right = result.top();
				result.pop();
				double left = result.top();
				result.pop();
				result.push(left + right);
				break;
			}
			case '-':
			{
				double right = result.top();//被减数
				result.pop();
				double left = result.top();//减数
				result.pop();
				result.push(left - right);
				break;
			}
			case '^':
			{
				double exp = result.top();//指数
				result.pop();
				double base = result.top();//底数
				result.pop();
				if (!base)
				{
					cout << "底数为零" << endl;
					exit(-1);
				}
				else
				{
					double end = 1;
					for (int i = 0; i < exp; i++)
					{
						end *= base;
					}
					result.push(end);
					break;
				}
			}
			default:
			{
				result.push(c - 48);
			}
		}
		index++;
	}
	return result.top();

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94

1.2 根据表达式求后缀表达式

表达式求值的核心就是将波兰式（一般常见的表达式）转化为逆波兰式（后缀表达式）。上面讲过了如何根据后缀表达式求解表达式的值，那么如何获得后缀表达式？可以用二叉树，也可以用栈，这里讲解用栈的方式。

首先看规则：

普通表达式转换为后缀表达式需要用到一个空栈（假设名为Optr）和一个空数组（数组名）

如果为 ‘0’~‘9’ 的字符，将其添加到 postexp 数组的末尾；
如果该字符为除 ‘(’ 和 ‘)’ 以外的运算符，将其与 Optr 栈顶的运算符进行优先级比较（如乘法高于加法），如果该运算符优先级高于或等于栈顶运算符，则将其入栈；反之，如果该运算符优先级小于或等于栈顶运算符，则将栈顶运算符出栈并添加到 postexp 数组的尾部，然后继续拿当前运算符同新的栈顶运算符做大小比较，以此类推。
如果该字符为 ‘(’ 运算符，直接入栈；如果为 ‘)’ 运算符，依次取 Optr 栈顶运算符并将其添加到 postexp 数组末尾，直到遇到 ‘(’ 字符为止（注意，‘(’ 字符也从栈顶取出，但不将其添加 postexp 数组中）。

依照以上处理过程，直到将普通表达式遍历完毕，如果 Optr 栈中仍有运算符，依次将它们出栈并添加到 postex数组尾部。最终，postexp 数组内存储的表达式就是转换后的后缀表达式。

总结一句：运算项直接放数组中，运算符压入栈中，只有遇到比栈顶运算符优先级低的或栈空才出栈放入数组中。括号单独考虑。

如此一来运算符优先级高的就紧随运算项，先运算。运算符优先级低的往往在后缀表达式最右边。

下面是表达式3 ! 4 2 * 1 5 - 2 ^ / +转换为后缀表达式的过程：（按序号看）

代码实现

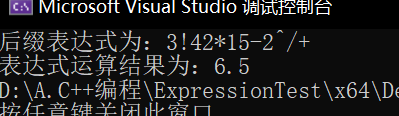
void transform(char* expr, char* out)
{
	stack<char>temp;
	int index = 0;//作为输出数组的下标
	int i = 0;//表达式的下标
	while(expr[i]!='\0')
	{
		char c = expr[i];
		switch (c)
		{
			case '!':
			{
				while (!temp.empty()) 
				{
					if (temp.top() == '!')
					{
						char ch = temp.top();
						temp.pop();
						out[index++] = ch;
					}
					else//说明优先级变高了，跳出循环直接入栈
					{
						break;
					}
				}
				temp.push('!');
				i++;
				break;
			}case '*':
			{
				while (!temp.empty())
				{
					if (temp.top() == '!' || temp.top() == '^' || temp.top() == '*' || temp.top() == '/')
					{
						char ch = temp.top();
						temp.pop();
						out[index++] = ch;
					}
					else//说明优先级变高了，跳出循环直接入栈
					{
						break;
					}
				}
				temp.push('*');
				i++;
				break;
			}case '/':
			{
				while (!temp.empty())
				{
					if (temp.top() == '!' || temp.top() == '^' || temp.top() == '*' || temp.top() == '/')
					{
						char ch = temp.top();
						temp.pop();
						out[index++] = ch;
					}
					else//说明优先级变高了，跳出循环直接入栈
					{
						break;
					}
				}
				temp.push('/');
				i++;
				break;
			}case '+':
			{
				while (!temp.empty())
				{
					if (temp.top() == '!' || temp.top() == '^' || temp.top() == '*' 
						|| temp.top() == '/' || temp.top() == '+' || temp.top() == '-')
					{
						char ch = temp.top();
						temp.pop();
						out[index++] = ch;
					}
					else//说明优先级变高了，跳出循环直接入栈
					{
						break;
					}
				}
				temp.push('+');
				i++;
				break;
			}case '-':
			{
				while (!temp.empty())
				{
					if (temp.top() == '!' || temp.top() == '^' || temp.top() == '*'
						|| temp.top() == '/' || temp.top() == '+' || temp.top() == '-')
					{
						char ch = temp.top();
						temp.pop();
						out[index++] = ch;
					}
					else//说明优先级变高了，跳出循环直接入栈
					{
						break;
					}
				}
				temp.push('-');
				i++;
				break;
			}case '(':
			{
				temp.push('(');
				i++;
				break;
			}case ')':
			{
				while (temp.top() != '(')
				{
					char ch = temp.top();
					temp.pop();
					out[index++] = ch;
				}
				temp.pop();//此时栈顶为（
				i++;
				break;
			}case '^':
			{
				while (!temp.empty())
				{
					if (temp.top() == '!'||temp.top()=='^')
					{
						char ch = temp.top();
						temp.pop();
						out[index++] = ch;
					}
					else//说明优先级变高了，跳出循环直接入栈
					{
						break;
					}
				}
				temp.push('^');
				i++;
				break;
			}default :
			{
				out[index++] = c;
				i++;
				break;
			}
		
		}
	}
	//此时将栈中多有的数据逐一出栈
	while (!temp.empty())
	{
		out[index++] = temp.top();
		temp.pop();
	}
	out[index] = '\0';//最后给后缀表达式加上尾\0
}
int main() {
	char* s = (char*)malloc(15 * sizeof(char));
	char* out = (char*)malloc(13 * sizeof(char));
	char temp[] = "3!+4*2/(1-5)^2";
	//cout << strlen(s);
	for (int i = 0; i < 15; i++)
	{
		s[i] = temp[i];
	}
	transform(s,out);
	cout << "后缀表达式为："<< out << endl;
	cout <<"表达式运算结果为："<< calculate(out);

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167

2. 二叉树求表达式值

2.1 二叉树存储表达式

表达式转换成二叉树的思路和栈其实类似，下面是具体算法思路

【算法步骤】

初始化OPTR栈和EXPT栈
按序逐个读取表达式字符。则循环执行以下操作。
- 若ch不是运算符，则以ch为根创建一棵只有根节点的二叉树，且将该树根节点压入EXPT栈。
- 若ch是运算符。若栈为空直接入栈，不用处理。若栈非空，则将ch运算符和根据OPTR的栈顶元素优先级比较结果，进行不同的处理；
  
  若ch优先级大于栈顶，则将ch压入OPTR栈
  
  若ch优先级小于或等于栈顶，则弹出OPTR栈顶的运算符，从EXPT栈弹出两个表达式子树的根节点。运算符为根节点，以EXPT栈中弹出的第二个子树作为左子树，以EXPT栈中弹出的第第一个子树作为右子树，创建一棵新二叉树并将该树根节点压入EXPT栈，成为新的表达式子树

此处的代码只考虑了±*/（），代码包括按序取字符，针对不同字符用switch语句处理，代码量主要就是在switch语句这里

#include
#include
using namespace std;

typedef char BTDataType;
struct BTNode {
	BTDataType data;
	BTNode* left;
	BTNode* right;
};

BTNode* newNode(BTDataType data) {
	BTNode* root = new BTNode;
	root->data = data;
	root->left = NULL;
	root->right = NULL;
	return root;
}
//将表达式换成对应的二叉树
BTNode* transform(string exp) {
	stack<char>OPTR;//运算符栈
	stack<BTNode*>EXPT;//表达式栈

	for (int i = 0; i < exp.size(); i++) {
		if (exp[i] >= 48 && exp[i] <= 57) {
			BTNode* root = newNode(exp[i]);
			EXPT.push(root);
		}
		else {
			if (OPTR.empty()||exp[i]=='(')OPTR.push(exp[i]);
			else {
				//考虑到的运算有：+-*/()
				switch (exp[i]) {
					case '*': {
						while (!OPTR.empty()) {
							char top = OPTR.top();
							if (top == '+' || top == '-' || top == '(') {
								//说明优先级变大或栈顶为（，直接进栈退出循环在循环外统一入栈
								break;
							}
							else {
								//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
								char top = OPTR.top();
								BTNode* root = newNode(top);
								OPTR.pop();

								//取得前两个表达式
								BTNode* exp1 = EXPT.top();
								EXPT.pop();
								BTNode* exp2 = EXPT.top();
								EXPT.pop();

								//左右子树链接
								root->left = exp2;
								root->right = exp1;
								
								//表达式压回栈
								EXPT.push(root);

							}
						}
						OPTR.push('*');
						break;
					}
					case '/': {
						while (!OPTR.empty()) {
							char top = OPTR.top();
							if (top == '+' || top == '-' || top == '(') {
								//说明优先级变大或栈顶为（，直接进栈退出循环和switch语句
								break;
							}
							else {
								//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
								char top = OPTR.top();
								BTNode* root = newNode(top);
								OPTR.pop();

								//取得前两个表达式
								BTNode* exp1 = EXPT.top();
								EXPT.pop();
								BTNode* exp2 = EXPT.top();
								EXPT.pop();

								//左右子树链接
								root->left = exp2;
								root->right = exp1;

								//表达式压回栈
								EXPT.push(root);

							}
						}
						OPTR.push('/');
						break;
					}
					case '-': {
						while (!OPTR.empty()) {
							char top = OPTR.top();
							if (top == '(') {
								//说明优先级变大或栈顶为（，直接进栈退出循环和switch语句
								OPTR.push('-');
								break;
							}
							else {
								//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
								char top = OPTR.top();
								BTNode* root = newNode(top);
								OPTR.pop();

								//取得前两个表达式
								BTNode* exp1 = EXPT.top();
								EXPT.pop();
								BTNode* exp2 = EXPT.top();
								EXPT.pop();

								//左右子树链接
								root->left = exp2;
								root->right = exp1;

								//表达式压回栈
								EXPT.push(root);

							}
						}
						OPTR.push('-');
						break;
					}
					case '+': {
						while (!OPTR.empty()) {
							char top = OPTR.top();
							if (top == '(') {
								//说明优先级变大或栈顶为（，直接进栈退出循环和switch语句
								break;
							}
							else {
								//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
								char top = OPTR.top();
								BTNode* root = newNode(top);
								OPTR.pop();

								//取得前两个表达式
								BTNode* exp1 = EXPT.top();
								EXPT.pop();
								BTNode* exp2 = EXPT.top();
								EXPT.pop();

								//左右子树链接
								root->left = exp2;
								root->right = exp1;

								//表达式压回栈
								EXPT.push(root);

							}
						}
						OPTR.push('+');
						break;
					}
					case '(': {
						OPTR.push('(');
						break;
					}
					case ')': {
						while (OPTR.top()!='(') {
							//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
							char top = OPTR.top();
							BTNode* root = newNode(top);
							OPTR.pop();

							//取得前两个表达式
							BTNode* exp1 = EXPT.top();
							EXPT.pop();
							BTNode* exp2 = EXPT.top();
							EXPT.pop();

							//左右子树链接
							root->left = exp2;
							root->right = exp1;

							//表达式压回栈
							EXPT.push(root);
						}
						OPTR.pop();//将（出栈
						break;
					}
				}
			}
		}
	}
	//此时将OPTR栈中所有的元素出栈，换称对应的表达式到EXPT中
	while (!OPTR.empty()) {
		//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
		char top = OPTR.top();
		BTNode* root = newNode(top);
		OPTR.pop();

		//取得前两个表达式
		BTNode* exp1 = EXPT.top();
		EXPT.pop();
		BTNode* exp2 = EXPT.top();
		EXPT.pop();

		//左右子树链接
		root->left = exp2;
		root->right = exp1;

		//表达式压回栈
		EXPT.push(root);
	}
	return EXPT.top();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211

2.2 用二叉树求表达式的值

表达式树的求值【算法步骤】

设变量lvalue和rvalue分别用以记录表达式树中左子树和右子树的值,初始均为0。
如果当前节点为叶子（节点为操作数），则返回该节点的数值,否则(节点为运算符）执行以下操作:
递归计算左子树的值，记为Ivalue;递归计算右子树的值,记为rvalue;
根据当前节点运算符的类型，将lvalue和rvalue进行相应运算并返回。

代码实现：

double valueBTree(BTNode* root)
{
	if (root->data >= 48 && root->data <= 57)return root->data-48;
	else {
		double lvalue = valueBTree(root->left);
		double rvalue = valueBTree(root->right);
		switch (root->data) {
			case '+': {
				return lvalue + rvalue;
				break;
			}
			case '-': {
				return lvalue - rvalue;
				break;
			}
			case '*': {
				return lvalue * rvalue;
				break;
			}
			case '/': {
				return lvalue / rvalue;
				break;
			}
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

2.3 二叉树求表达式完整测试代码

#include
#include
using namespace std;

typedef char BTDataType;
struct BTNode {
	BTDataType data;
	BTNode* left;
	BTNode* right;
};

BTNode* newNode(BTDataType data) {
	BTNode* root = new BTNode;
	root->data = data;
	root->left = NULL;
	root->right = NULL;
	return root;
}
//将表达式换成对应的二叉树
BTNode* transform(string exp) {
	stack<char>OPTR;//运算符栈
	stack<BTNode*>EXPT;//表达式栈

	for (int i = 0; i < exp.size(); i++) {
		if (exp[i] >= 48 && exp[i] <= 57) {
			BTNode* root = newNode(exp[i]);
			EXPT.push(root);
		}
		else {
			if (OPTR.empty()||exp[i]=='(')OPTR.push(exp[i]);
			else {
				//考虑到的运算有：+-*/()
				switch (exp[i]) {
					case '*': {
						while (!OPTR.empty()) {
							char top = OPTR.top();
							if (top == '+' || top == '-' || top == '(') {
								//说明优先级变大或栈顶为（，直接进栈退出循环在循环外统一入栈
								break;
							}
							else {
								//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
								char top = OPTR.top();
								BTNode* root = newNode(top);
								OPTR.pop();

								//取得前两个表达式
								BTNode* exp1 = EXPT.top();
								EXPT.pop();
								BTNode* exp2 = EXPT.top();
								EXPT.pop();

								//左右子树链接
								root->left = exp2;
								root->right = exp1;
								
								//表达式压回栈
								EXPT.push(root);

							}
						}
						OPTR.push('*');
						break;
					}
					case '/': {
						while (!OPTR.empty()) {
							char top = OPTR.top();
							if (top == '+' || top == '-' || top == '(') {
								//说明优先级变大或栈顶为（，直接进栈退出循环和switch语句
								break;
							}
							else {
								//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
								char top = OPTR.top();
								BTNode* root = newNode(top);
								OPTR.pop();

								//取得前两个表达式
								BTNode* exp1 = EXPT.top();
								EXPT.pop();
								BTNode* exp2 = EXPT.top();
								EXPT.pop();

								//左右子树链接
								root->left = exp2;
								root->right = exp1;

								//表达式压回栈
								EXPT.push(root);

							}
						}
						OPTR.push('/');
						break;
					}
					case '-': {
						while (!OPTR.empty()) {
							char top = OPTR.top();
							if (top == '(') {
								//说明优先级变大或栈顶为（，直接进栈退出循环和switch语句
								OPTR.push('-');
								break;
							}
							else {
								//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
								char top = OPTR.top();
								BTNode* root = newNode(top);
								OPTR.pop();

								//取得前两个表达式
								BTNode* exp1 = EXPT.top();
								EXPT.pop();
								BTNode* exp2 = EXPT.top();
								EXPT.pop();

								//左右子树链接
								root->left = exp2;
								root->right = exp1;

								//表达式压回栈
								EXPT.push(root);

							}
						}
						OPTR.push('-');
						break;
					}
					case '+': {
						while (!OPTR.empty()) {
							char top = OPTR.top();
							if (top == '(') {
								//说明优先级变大或栈顶为（，直接进栈退出循环和switch语句
								break;
							}
							else {
								//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
								char top = OPTR.top();
								BTNode* root = newNode(top);
								OPTR.pop();

								//取得前两个表达式
								BTNode* exp1 = EXPT.top();
								EXPT.pop();
								BTNode* exp2 = EXPT.top();
								EXPT.pop();

								//左右子树链接
								root->left = exp2;
								root->right = exp1;

								//表达式压回栈
								EXPT.push(root);

							}
						}
						OPTR.push('+');
						break;
					}
					case '(': {
						OPTR.push('(');
						break;
					}
					case ')': {
						while (OPTR.top()!='(') {
							//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
							char top = OPTR.top();
							BTNode* root = newNode(top);
							OPTR.pop();

							//取得前两个表达式
							BTNode* exp1 = EXPT.top();
							EXPT.pop();
							BTNode* exp2 = EXPT.top();
							EXPT.pop();

							//左右子树链接
							root->left = exp2;
							root->right = exp1;

							//表达式压回栈
							EXPT.push(root);
						}
						OPTR.pop();//将（出栈
						break;
					}
				}
			}
		}
	}
	//此时将OPTR栈中所有的元素出栈，换称对应的表达式到EXPT中
	while (!OPTR.empty()) {
		//说明优先级变小或相等，创建二叉树，表达式栈前两个为其左右子树
		char top = OPTR.top();
		BTNode* root = newNode(top);
		OPTR.pop();

		//取得前两个表达式
		BTNode* exp1 = EXPT.top();
		EXPT.pop();
		BTNode* exp2 = EXPT.top();
		EXPT.pop();

		//左右子树链接
		root->left = exp2;
		root->right = exp1;

		//表达式压回栈
		EXPT.push(root);
	}
	return EXPT.top();
}

double valueBTree(BTNode* root)
{
	if (root->data >= 48 && root->data <= 57)return root->data-48;
	else {
		double lvalue = valueBTree(root->left);
		double rvalue = valueBTree(root->right);
		switch (root->data) {
			case '+': {
				return lvalue + rvalue;
				break;
			}
			case '-': {
				return lvalue - rvalue;
				break;
			}
			case '*': {
				return lvalue * rvalue;
				break;
			}
			case '/': {
				return lvalue / rvalue;
				break;
			}
		}
	}
}
int main() {
	string sample = "(1+2)*3-4/5";
	BTNode* root =transform(sample);
	cout << endl;
	cout << "输入：" << sample << endl;
	cout << "输出" << valueBTree(root) << endl;

	sample = "1+2*3-4/5";
	root = transform(sample);
	cout << endl;
	cout << "输入：" << sample << endl;
	cout << "输出" << valueBTree(root) << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251

相关阅读:
软考 - 计算机组成与结构
 idea 超实用的插件
 银行卡二元素api接口是怎么完成验证的？
3D Object Proposals for Accurate Object Class Detection
VM16中安装CentOS7.4保姆级教程
 UE4 自定义组件编译成功，但是无法在添加到 Actor(Add to Actor) 中找到，无法拖动到 Actor 中附加到 Root 的解决方法
 前端面试题（JS部分）
Python 潮流周刊第 39 期（摘要）
【设计模式】Java设计模式 - 桥接模式
 【无标题】
原文地址：https://blog.csdn.net/weixin_63267854/article/details/128083840