【机器学习】推荐系统

推荐系统的工作原理

推荐模型如何进行推荐将取决于您拥有的数据类型。如果您只拥有过去发生的交互数据，您可能有兴趣使用协作过滤。如果您有描述用户及其与之交互过的物品的数据（例如，用户的年龄、餐厅的菜系、电影的平均评价），您可以通过添加内容和上下文过滤，对当前给定这些属性下新交互的可能性进行建模。

推荐系统中最为主流与经典的技术之一是协同过滤技术（Collaborative Filtering），它是基于这样的假设：用户如果在过去对某些项目产生过兴趣，那么将来他很可能依然对其保持热忱。其中协同过滤技术又可根据是否采用了机器学习思想建模的不同划分为基于内存的协同过滤（Memory-based CF）与基于模型的协同过滤技术（Model-based CF）。其中基于模型的协同过滤技术中尤为矩阵分解（Matrix Factorization）技术最为普遍和流行，因为它的可扩展性极好并且易于实现.

对于推荐系统来说存在两大场景即评分预测（rating prediction）与Top-N推荐（item recommendation，item ranking）

推荐系统类型

虽然有许多推荐算法和技术，但大多数都属于以下广泛类别：协作过滤、内容过滤和上下文过滤。

• 协作过滤算法根据许多用户的偏好信息（这是协作部分）推荐物品（这是过滤部分）。此方法使用用户偏好行为的相似性，并鉴于用户与物品之间的之前交互，推荐算法便可以学会预测未来交互。这些推荐系统基于用户过去的行为构建模型，例如之前购买的物品或给予这些物品的评分以及其他用户的类似决策。相关理念在于，如果有些人过去也做出过类似的决策和购买，比如电影选择，那么他们很有可能会同意未来的其他选择。例如，如果协作过滤推荐系统了解您和另一个用户在电影中有着相似的品味，它可能会向您推荐一部其了解的其他用户已经喜欢的电影。
• 内容过滤使用物品的属性或特征（这是内容部分）来推荐类似于用户偏好的其他物品。此方法基于物品和用户特征的相似性，并鉴于用户及其与之交互过的物品的信息（例如，用户的年龄、餐厅的菜系、电影的平均评价），来模拟新互动的可能性。例如，如果内容过滤推荐系统了解到您喜欢电影《电子情书》和《西雅图夜未眠》，它可能会向您推荐另一部相同类别和/或演员阵容的电影，例如《跳火山的人》。
• 上下文过滤包括推荐过程中用户的背景信息。Netflix 在 NVIDIA GTC 大会上提出，将推荐内容框定为上下文序列预测，以便作出更好的推荐。此方法使用一系列上下文用户操作和当前上下文来预测下一个操作的概率。在 Netflix 示例中，鉴于每位用户的序列（用户在观看电影时的国家/地区、设备、日期和时间），他们训练出一个模型，来预测用户接下来要观看的内容。

传统的方法: 矩阵分解法MF (matrix factorization)

1. 矩阵因子分解（MF）

推荐系统评分预测任务可看做是一个矩阵补全（Matrix Completion）的任务，即基于矩阵中已有的数据（observed data）来填补矩阵中没有产生过记录的元素（unobserved data）。推荐系统的评分预测场景可看做是一个矩阵补全的游戏，矩阵补全是推荐系统的任务，矩阵分解是其达到目的的手段。因此，矩阵分解是为了更好的完成矩阵补全任务（假设UI矩阵是低秩的）

MF方法的局限性：
在低维的隐式空间中建模用户、项目的embedding，而且使用简单、不够灵活的内积的方式来估计复杂的用户-项目之间的关系（内积的方式是对用户、项目向量中元素的简单的线性组合）。虽然可以通过增加隐式空间的维度来提升推荐效果，但是在数据稀疏（Sparse）的情况下，会导致过拟合。

2. SVD奇异值分解

SVD分解的形式为3个矩阵相乘，左右两个矩阵分别表示用户/项目隐含因子矩阵，中间矩阵为奇异值矩阵并且是对角矩阵，每个元素满足非负性，并且逐渐减小。因此我们可以只需要前 k 个因子来表示它。

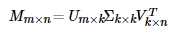
如果想运用SVD分解的话，有一个前提是要求矩阵是稠密的，即矩阵里的元素要非空，否则就不能运用SVD分解。很显然我们的任务还不能用SVD，所以一般的做法是先用均值或者其他统计学方法来填充矩阵，然后再运用SVD分解降维。 

3. FunkSVD算法（LFM）

SVD首先需要填充矩阵，然后再进行分解降维，同时由于需要求逆操作（复杂度O(n^3)），存在计算复杂度高的问题。那么我们能不能避开稀疏问题，同时只分解成两个矩阵呢？

这种简化的矩阵分解不再是分解为三个矩阵，而是分解为两个低秩的用户和物品矩阵，其实就是把用户和物品都映射到一个 k 维空间中，这个 k 维空间对应着 k 个隐因子，我们认为用户对物品的评分主要是由这些隐因子影响的，所以这些隐因子代表了用户和物品一部分共有的特征，在物品身上表现为属性特征，在用户身上表现为偏好特征。
FunkSVD采用了线性回归的思想将矩阵R分解为P和Q。我们的目标是让用户的评分和用矩阵乘积得到的评分残差尽可能的小，也就是说，可以用均方差作为损失函数，来寻找最终的P和Q。即通过 User-Item 评分信息来学习到的用户特征矩阵 P 和物品特征矩阵 Q，通过重构的低维矩阵预测用户对物品的评分

协同过滤 Collaborative Filtering

使用用户历史的行为来做未来的推荐。忽略了关于用户或item的先验信息。

    CF使用与我相似的用户的评分来预测我的评分
    CF是领域无关的，不需要知道现在在对什么评分，谁在评分，评分是多少

一种CF方法称为基于邻域的方法。例如

    定义一个相似度评分，基于用户之间评分的重叠度
    基于相似度评分，使用邻域内的评分来为我喜欢的item打分

过滤方法并不是互斥的。内容信息可以被添加到协同过滤系统来提升性能。

协同过滤的主要缺点：

• 协同过滤处理稀疏矩阵的能力较弱（共现矩阵稀疏，泛化能力弱）
• 协同过滤中相似度矩阵维护难度大（维度高）

神经协作过滤 (NCF) Neural Collaborative Filtering

神经协作过滤 (NCF) 模型是一个神经网络，可基于用户和物品交互提供协作过滤。该模型从非线性角度处理矩阵分解。NCF TensorFlow 以一系列（用户 ID、物品 ID）对作为输入，然后分别将其输入到矩阵分解(MF)步骤（其中嵌入成倍增加）并输入到多层感知器 (MLP) 网络中。

然后，将矩阵分解和 MLP 网络的输出将组合到一个密集层中，以预测输入用户是否可能与输入物品交互。

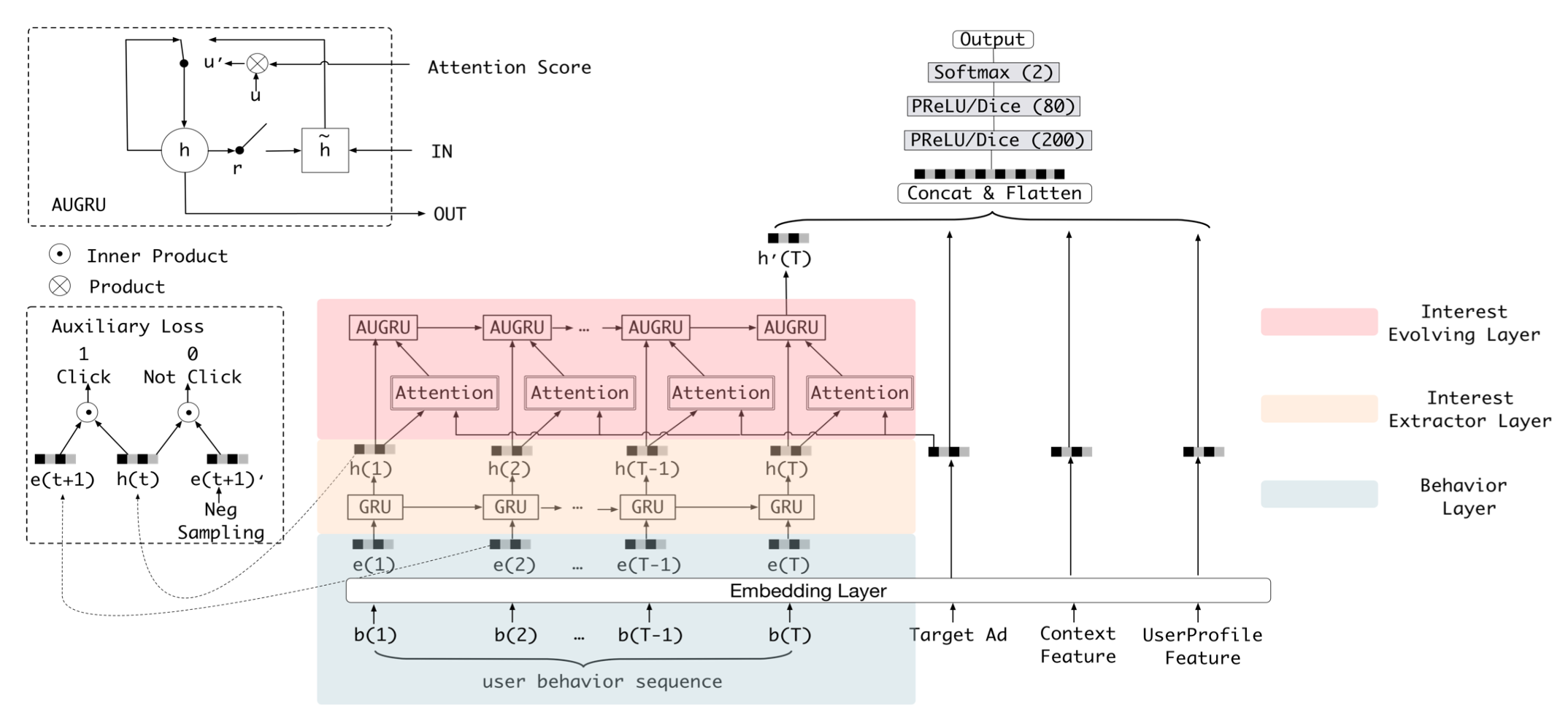
DIEN模型（Deep Interest Evolution Network）

References

推荐系统之矩阵分解家族 - 知乎

协同过滤的进化--矩阵分解算法（MF）_【敛芳尊】的博客-CSDN博客_协同过滤mf