【POJ No. 3067】 公路交叉数 Japan

【POJ No. 3067】 公路交叉数 Japan

北大 OJ 题目地址

【题意】

东海岸有N 个城市，西海岸有M 个城市（N ≤1000，M ≤1000），将建成K 条高速公路。每个海岸的城市从北到南编号为1, 2, ……每条高速公路都是直线，连接东海岸的城市和西海岸的城市。建设资金由高速公路之间的交叉数决定。

两个高速公路最多在一个地方交叉。请计算高速公路之间的交叉数量。

【输入输出】

输入：

输入文件以T 为开头，表示测试用例的数量。每个测试用例都以3个数字N 、M 、K 为开头。下面K 行中的每一行都包含两个数字，表示由高速公路连接的城市号。

第1个是东海岸的城市号，第2个是西海岸的城市号。

输出：

对每个测试用例，都单行输出“Test case x : s ”，x表示输入样例编号，s 表示交叉数。

【样例】

【思路分析】

根据输入样例分析，一共有5个交叉点。

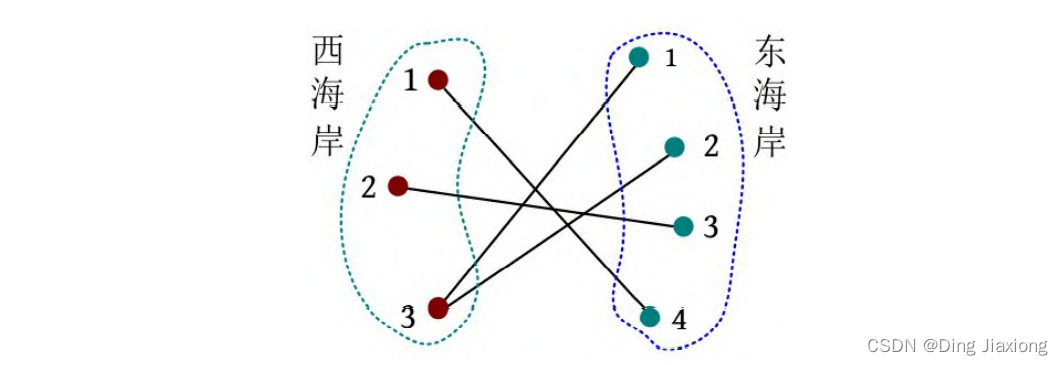
那么，怎么求交叉点呢？首先搞清楚交叉点是怎么产生的。当两条边的城市号都以升序（或降序）形式出现时，不产生交叉点。例如1 2和2 3不会产生交叉点

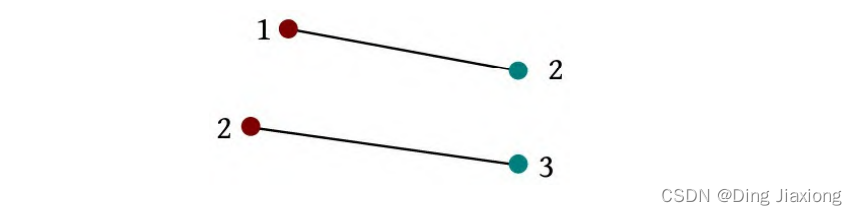
1 4和2 3会产生交叉点，因为西海岸城市1、2是升序的，东海岸城市4、3是降序的。

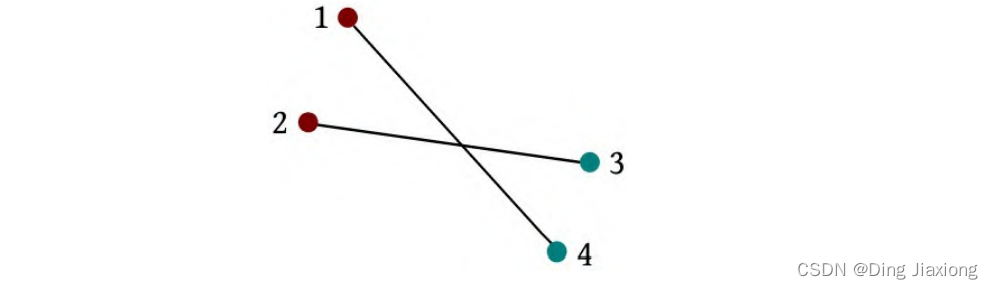
因此交叉点的产生原因和逆序对有关系，所以转变为求解逆序对问题。

【算法设计】

① 对输入的边按照x 升序排列，若x 相等，则按y 升序排列。

② 检查每条边i ，统计y 的前缀和sum(e[i ].y )，该前缀和是前面比y 小的正序数，边数减去正序数，即可得到逆序数i -sum(e[i].y )，ans累加逆序数。

③ 将树状数组中e[i ].y 的值加1。

【举个栗子】

根据输入样例，其交叉点求解过程如下。

① 对输入的边按照x 升序，若x 相等，则按y 升序。

排序结果：

② 按照排序结果检查每条边i ，统计y 的前缀和sum(e[i ].y)，将ans累加i -sum(e[i ].y )。

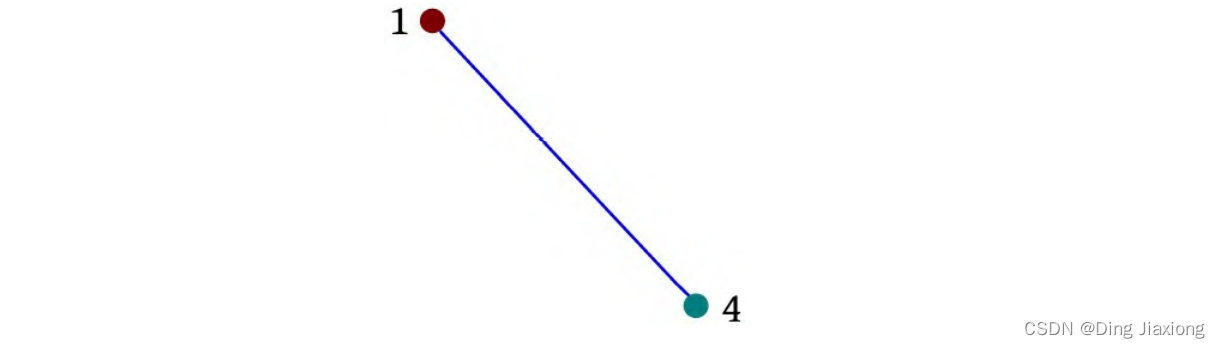
• i =0：1 4=。sum(4)0，i -sum(4)=0；1的前缀和为0，说明1前面没有数，因为前面还没有输入边，所以逆序边数量ans=0。
  

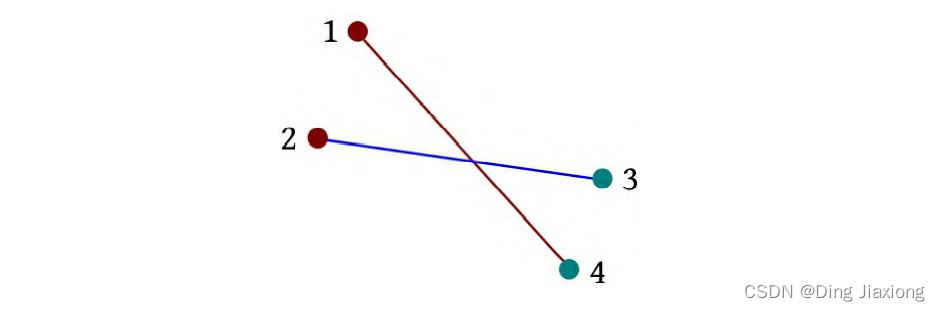
• i =1：2 3。sum(3)=0，i -sum(3)=1。3的前缀和为0，说明3前面没有数，所以前面的1条边是逆序的，当前边和逆序边会产生交叉点，累加逆序边数量ans=1。
  

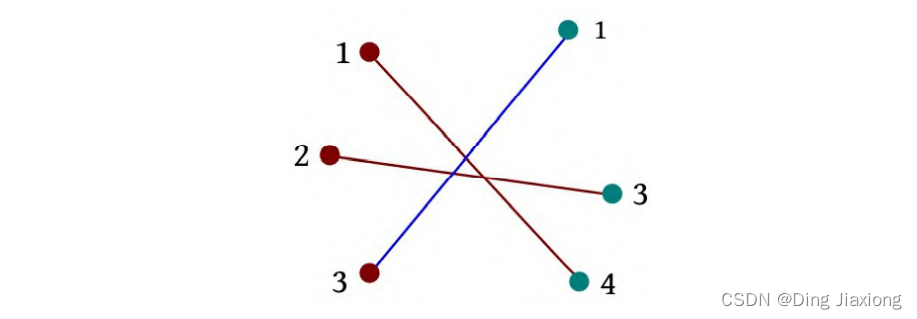
• i =2：3 1。sum(1)=0，i -sum(1)=2。1的前缀和为0，说明1前面没有数，因此前面的两条边是逆序的，当前边和每条逆序边会产生交叉点，累加逆序边数量ans=3。
  

• i =3：3 2。sum(2)=1，i -sum(2)=2；前面的3条边已经有1条边是正序的，将该边减去，其余两条边是逆序的，当前边和每个逆序边都会产生交叉点，累加逆序边数量ans=5。
  

【算法实现】

#include
#include
#include
#define maxn 1010
#define maxk 1000010
#define lowbit(x) (x)&(-x)

int c[maxn],kas,n,m,k;

using namespace std;

typedef long long LL;
struct Edge {
    int x, y;
}e[maxk];

bool cmp(Edge a,Edge b)
{
    return a.x<b.x||(a.x==b.x&&a.y<b.y);
}

void add(int i)//加1操作，参数省略
{
    while(i<=m)//y点有m个
	{
        ++c[i];
        i+=lowbit(i);
    }
}

int sum(int i)
{
    int s=0;
    while(i>0)
	{
        s+=c[i];
        i-=lowbit(i);
    }
    return s;
}

int main()
{
    int T;
    scanf("%d",&T);
    while (T--)
	{
		memset(c,0,sizeof(c));
	    scanf("%d%d%d",&n,&m,&k);
	    for(int i=0;i<k;i++)
			scanf("%d%d",&e[i].x,&e[i].y);
	    sort(e,e+k,cmp);
	    LL ans=0;
	    for(int i=0;i<k;i++){
	        ans+=i-sum(e[i].y);
	        add(e[i].y);
	    }
	    printf("Test case %d: %lld\n",++kas,ans);
	}
	
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63