毫米波传感器原理介绍：测距

本篇文章介绍了毫米波传感器测距的一种原理，帮助嵌入式工程师在做雷达编程的时候能够对SDK代码有更清晰的认知，可以对测距部分逻辑进行修改和裁剪。

因为本篇是第一篇关于毫米波雷达传感器设备的介绍，我便多啰嗦两句。近几年随着无人驾驶等领域在国内的火热，做支撑实现无人驾驶的智能设备也多了起了，首当其冲的便是无人驾驶的眼睛“摄像头”，同样作为一种辅助手段的雷达技术也被应用到了无人驾驶应用领域。目前应用在车载领域的毫米波雷达按实现方式的不同只要分为毫米波雷达（lidar），毫米波雷达（Millimeter-WaveRadar）以及超声波雷达（ultrasonicradar）。各种雷达在探测距离，精度，环境影响等都各有千秋。
本篇主要介绍的相关应用原理主理针对的是毫米波雷达在车载领域的不同场景应用，如下图所示。资料来源为Ti官网上的一些培训课程。

一、测距关键概念/公式

要想把测距这部分的应用原理有个认识，下面三个公式必须熟悉。我先把公式抛出来，供大家在后边的介绍慢慢理解。

1. 回波中频等于调频斜率乘以两倍目标距离除以光速。$\frac{S2d}{c}=f_{IF}$
2. 距离分辨率等于光速除以两倍带宽（线性调频脉冲带宽）。$\frac{c}{2B}=d_{res}$
3. ADC采样频率限制的最远距离为采样频率乘以光速除以线性调频斜率。$\frac{F_{s}c}{S}=d_{max}$

还有一个概念我们需要区分，就是射频带宽和IF 带宽。射频带宽是线性调频脉冲跨越的带宽。较大的射频带宽可直接转换为较好的距离分辨率。射频带宽的范围通常为几百 MHz至几 GHz。例如，4GHz 的射频带宽可转换为 4 厘米的距离分辨率。400MHz 的射频带宽可转换为大约 30 厘米的距离分辨率。另一种带宽是 IF 带宽。较大的 IF 带宽主要可以使雷达看到较大的最大距离。还可以实现较快的线性调频脉冲。我说较快的线性调频脉冲，是指具有较高斜率的线性调频脉冲。典型雷达的IF 带宽处于低 MHz 范围内。那么，这是有关FMCW 雷达的要点之一，您可以具有跨越较大带宽的射频信号，比如 4GHz，但您的 ADC仅需要对几 MHz 的信号进行采样。

二、FMCW雷达概念前述

在讲雷达测距工作测距原理之前，我们先思考一下三个问题：

1. 雷达是如何估计物体的距离？
2. 雷达是如何识别多个目标？
3. 两个目标靠多近，雷达依然可以分辨出来？
   一下是我们讨论三个问题涉及的模型：
   
   本篇文章主要围绕着这三个问题对FMCW雷达在测距功能方面进行讨论。
   首先，我们需要了解什么是chirp信号（线性调频脉冲）。chrip信号是随时间线性增长的正弦波，类似小鸟的叫声一般，频率在整个鸣叫的过程不断升高，其信号的时域波形如下图所示：
   
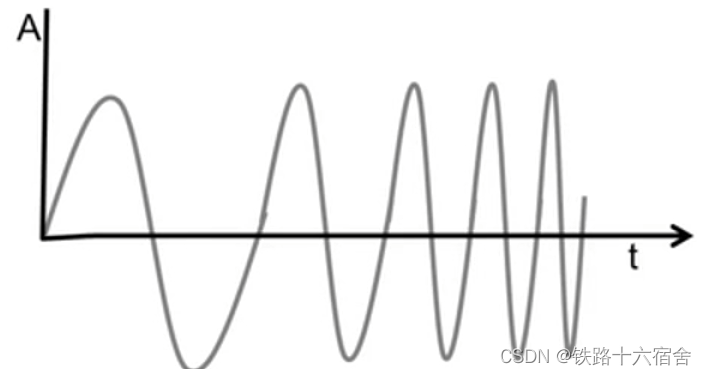
   我们建设正弦的初始频率为$f_c$,最终结束以频率$f_c$+B结束，那么B即为chrip信号的带宽，也就是前面提到的射频带宽。确定一个chrip信号只需要起始频率$f_c$，脉冲时长$T_c$以及射频带宽B即可。下图为$f_c=77Hhz$，$40us$跨越带宽为$4GHz$，最终频率为81GHz的chrip信号时域图。其中S代表脉冲频率随时间变化的斜率。
   
   下图为一个简化的一发一收的FMCW雷达系统组成框图。该雷达的工作原理如下，合成器（1）生成一个线性调频脉冲，通过发送天线（2）将脉冲发出去，当脉冲遇到物体后，该脉冲会反射回来被Rx天线（3）接收。将Rx的回波信号和Tx信号进行混频（4）处理，最终生成中频信号（IF信号），我们对IF信号进行处理来提取出我们需要信息。
   
   所谓的混频器，就是输出的瞬时频率等于所有输入信号瞬时频率的差值，初始相位等于输入信号的相位差。
   

三、FMCW雷达目标距离检测原理（单目标）

发射的脉冲和遇到目标反射的脉冲皆为线性调频脉冲，接收信号相当于发送信号的延时版本，如下图：

根据上面介绍的雷达系统组成组成框图，混频器的输入为发射信号和接收信号，经过混频器处理后，我们得到了中频信号，其频率为发射信号和接收信号的频率差，初始相位为发射相位和接收相位的初始相位差，所以IF中频信号在f-t的表示形式如下图中第二个时域图。
那么，为了生成中频信号的时域图，我需要将RX chrip的信号减去TX chrip信号,即为上面介绍的中频信号。正如您看到的，这两条线相互之间存在固定的距离。该固定的距离由线性调频脉冲的斜率乘以往返延迟给出。因此，雷达前方的单个物体可生成一个包含单个频率的IF 信号，该频率由 $S\ast \tau$给出。现在$\tau$，即从雷达到物体然后又返回的往返延迟，也可以表示为与物体的距离除以光速，然后乘以 2。那么，这是需要记住的基本概念。雷达前方的单个物体可生成具有恒定频率的 IF信号，该频率由$\frac{S2d}{c}$公式计算得到。 这也是我们前文提到的第一个公式。

针对后续需要对中频信号使用DAC进行采样，必须确保在发射信号之后，仅仅经过$\tau$时间就对该信号进行采样，且在发送信号发送完毕截至。延时时间$\tau$通常是总线性调频脉冲时间的很小一部分。例如，对于最大距离为 300 米并且线性调频脉冲时间为 40 微秒的雷达，该 τ 与 Tc 的比率仅为 5%。

四、傅里叶变换知识点补充

首先，傅里叶变换能将信号从时域转化到频域。

​ 常规来说在时域单个频率的信号会在频域中生成一个峰值，在时域存在两个频率的信号会在频域生成两个峰值。但是，我们模拟两个正弦波，在观测窗口中T，红色的信号出现了2个周期，而蓝色的信号出现了2.5个周期，红色信号和蓝色信号之间的存在0.5周期，他的FFT结果如右边所示，并没有区分出来两个信号。

现在我们把观测窗口增大为2T，红色信号和蓝色信号之间的差值为一个周期，则可在频域中成功的解析这两个峰值。

通过这次模拟实验，我们可以得出一个重要结论，即观测期（或者观测窗口）越长，傅里叶解析的效果越好。

五、多个目标的检测原理

在毫米波雷达的实际应用中，往往是对多个目标进行检测。和单个目标一样，当雷达发送线性调频脉冲到多个目标后会返回多个线性调频脉冲，每一个脉冲都有不同量的延时。 由于信号频率和物体距离d是正比例的线性关系，所以频率越低距离雷达距离越近，反之越远。 使用傅里叶变化可以区分出不同目标的频率。如下图。

​ 通过目前的分析可以了解雷达是如何对物体距离进行计算和雷达是如何识别多个目标。两个目标靠多近，雷达就无法分辨两个不同的目标了？这其实就是雷达距离分辨率的概念。

六、雷达距离分辨率

我们先考虑两个靠近目标的时域和频域图，由下图可知道。A-t信号出现两个正弦波，分别为两个目标的中频信号，如果物体很近，可能就会造成在频谱中只出现一个单个峰值的现象，这个时候就无法区分两个目标，频谱下图右侧所示。那么这个两个物体距离最近为多少时，可以区分出两个信号了?

推到距离分辨率由一下两个基本公式，假设有两个在极限距离的物体，他们两个间距根据我们开篇的第一个公式为$\Delta f=\frac{S2\Delta d}{c}$。
第二个基本公式是基于为了能在频谱上区分这两个信号，那么这两个中频信号的频率差应大于射频带宽频率差（$T_c$的倒数），即为$\Delta f>\frac{1}{T_c}$。
根据这两个公式，即可得出距离分辨率大于光速除以两倍的带宽$\Delta d>\frac{c}{2B}$,则可以得出我们的第二个公式$\frac{c}{2B}=d_{res}$ 。

七、雷达最远距离

我们先引入一个思考，对比下图两个调频脉冲信号，hirp A和chirp B有相同的带宽，所以两者具有相同的距离分辨率，但是chirp A有chirp B两倍的观测窗口，所以从傅里叶变换的分辨率来说，chirp A信号的分辨率应该好于chirp B信号，除此之外了，还有什么区别吗？答案是肯定的，斜率在毫米波雷达中跟最远距离有一定关系。

我们已知IF信号的频率和距离呈正比关系，在大多数毫米波的雷达方案中，为了提取中频信号的信息，我们会先对中频信号进行数字化处理，首先中频信号会通过低通滤波器，然后使用ADC对其进行采样，然后使用合适的DSP或者MCU进行后续的处理。数字化的处理过程如下图所示。

假设需要检测物体的最大距离为$d_{max}$,那么根据最一开始第一个公式可以得出$\frac{S2d_{max}}{c}=f_{IFmax}$,adc的采样率最小应该等于最大的中频频率（IQ双路采集，如果是直接采集那么Adc采样频率理论是中频2倍，实际使用一般是2.4倍以上），即为$F_{mins}=\frac{S2d_{max}}{c}$，，
由于 A 和 B 具有相同的带宽，因此它们当然具有相同的距离分辨率。但是，请注意，线性调频脉冲 A 的斜率是 B 的一半。因此，根据上面的公式。对于相同的最大距离要求，或对于相同的 dmax，线性调频脉冲 A仅需要一半的 IF带宽，这意味着 ADC具有较小的采样率。因此，线性调频脉冲A 具有 ADC 要求更宽松的优势，而线性调频脉冲 B 当然也具有仅需要一半测量时间的优势。因为ADC的采样速率问题以及后续adc数据处理RAM大小的问题，如果ADC采样率和 IF带宽是传感器的瓶颈，那么可以通过调整斜率或者最大距离来进行折中设计，通常，雷达倾向于针对较大的 dmax时，使用较小的斜率。

十六宿舍 原创作品，转载必须标注原文链接。
©2023 Yang Li. All rights reserved.
欢迎关注 『十六宿舍』，大家喜欢的话，给个👍，更多关于嵌入式相关技术的内容持续更新中。