数据结构学习笔记（V）：树与二叉树

目录

1 树

1.1 树的定义和基本术语

1.定义

2.基本术语

1.2 树的性质

2 二叉树

2.1 二叉树的定义和基本术语

1.定义

2.特殊二叉树

2.2 二叉树性质

2.3 二叉树存储结构

1.顺序存储

2.链式存储

3 二叉树进阶

3.1 二叉树顺序遍历

1.先序遍历

2.中序遍历

3.后序遍历

3.2 二叉树层次遍历

3.3 遍历序列构造二叉树

1.前序+中序

2. 后序+中序

3.层序+中序

3.4 线索二叉树

1.二叉树的中序遍历序列

2.线索二叉树作用

2.对比

3.5 二叉树线索化

1.中序线索化

2.先序线索化

3.后序线索化

3.6 线索二叉树前驱后继 

4 树和森林

4.1 树的存储结构

1.双亲表示法

2.孩子表示法

3.孩子兄弟表示法

4.2 树和森林的遍历

1.树的遍历

2.森林遍历

5 二叉树应用

5.1 二叉排序树

1.定义

2.查找

3.插入

4.构造

5.删除

6.查找效率分析

5.2 平衡二叉树

1.定义

2.不平衡问题调整

3.查找效率分析

5.3 哈夫曼树

1.带权路径长度

2.定义

3.构造

4.哈夫曼编码

---

1 树

1.1 树的定义和基本术语

1.定义

2.基本术语

·属性

结点的层次：从上往下；结点的高度：从下往上；树的高度：层数；结点的度：分支数；树的度：各结点度的最大值

·有序树

树中各结点子树从左至右是有次序的，可以互换。无序树与之相反。 

·森林

森林是m棵互不相交的树都集合

1.2 树的性质

1.结点数 = 总度数 + 1

2.m叉树：每个结点最多只能有m个分支的树，允许所有结点的度 < m，且可以是空树

3.度为m的树第i层至多有m^(i-1)个结点

4.

 5.

 

 6.

2 二叉树

2.1 二叉树的定义和基本术语

1.定义

2.特殊二叉树

·满二叉树：一棵高度为h，且含有2^h - 1个结点的二叉树

·完全二叉树：

  

·二叉排序树

左子树所有结点关键字均小于根结点的关键字；右子树所有结点关键字均大于根结点的关键字

·平衡二叉树

树上任一结点的左子树和右子树的深度之差不超过1

2.2 二叉树性质

·二叉树性质

·完全二叉树性质

2.3 二叉树存储结构

1.顺序存储

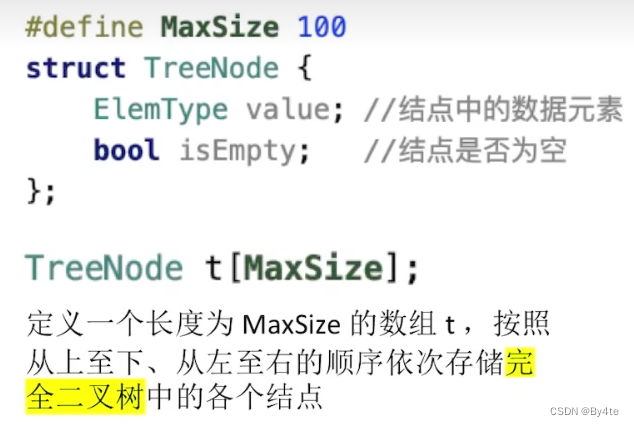
普通二叉树的顺序存储中，要将二叉树的结点编号与完全二叉树对应起来，但会导致存储空间浪费。

2.链式存储

 n个结点的二叉链表有n+1个空链域

3 二叉树进阶

3.1 二叉树顺序遍历

1.先序遍历

根左右-->前缀表达式

2.中序遍历

左根右-->中缀表达式（需加界限符）

3.后序遍历

左右根-->后缀表达式

3.2 二叉树层次遍历

3.3 遍历序列构造二叉树

顺序遍历不能唯一确定一棵二叉树

1.前序+中序

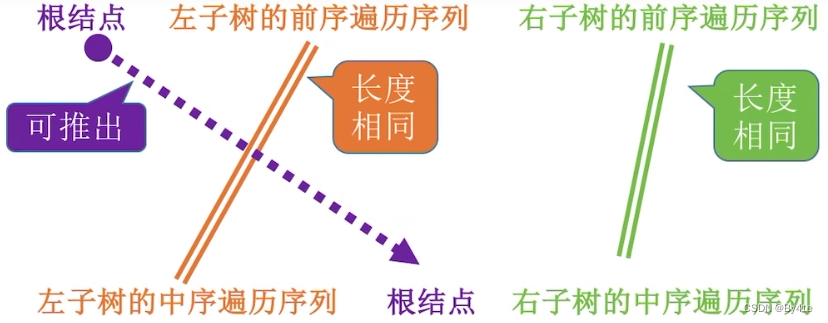
2. 后序+中序

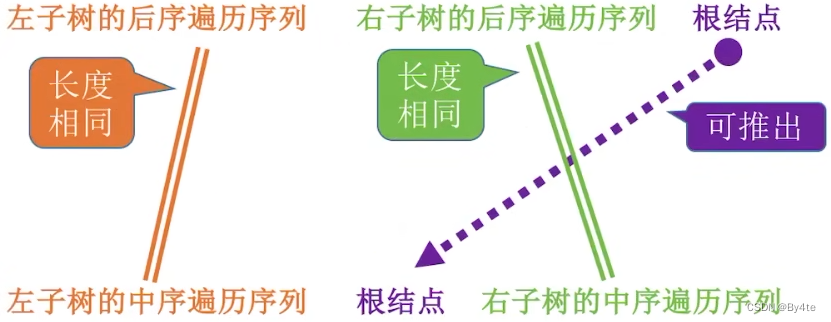
3.层序+中序

3.4 线索二叉树

1.二叉树的中序遍历序列

 缺点：遍历操作从根开始，寻找前驱与后继不方便

2.线索二叉树作用

中序

 左右线索标志，tag == 0，指针指向孩子；tag == 1，指针指向线索

2.对比

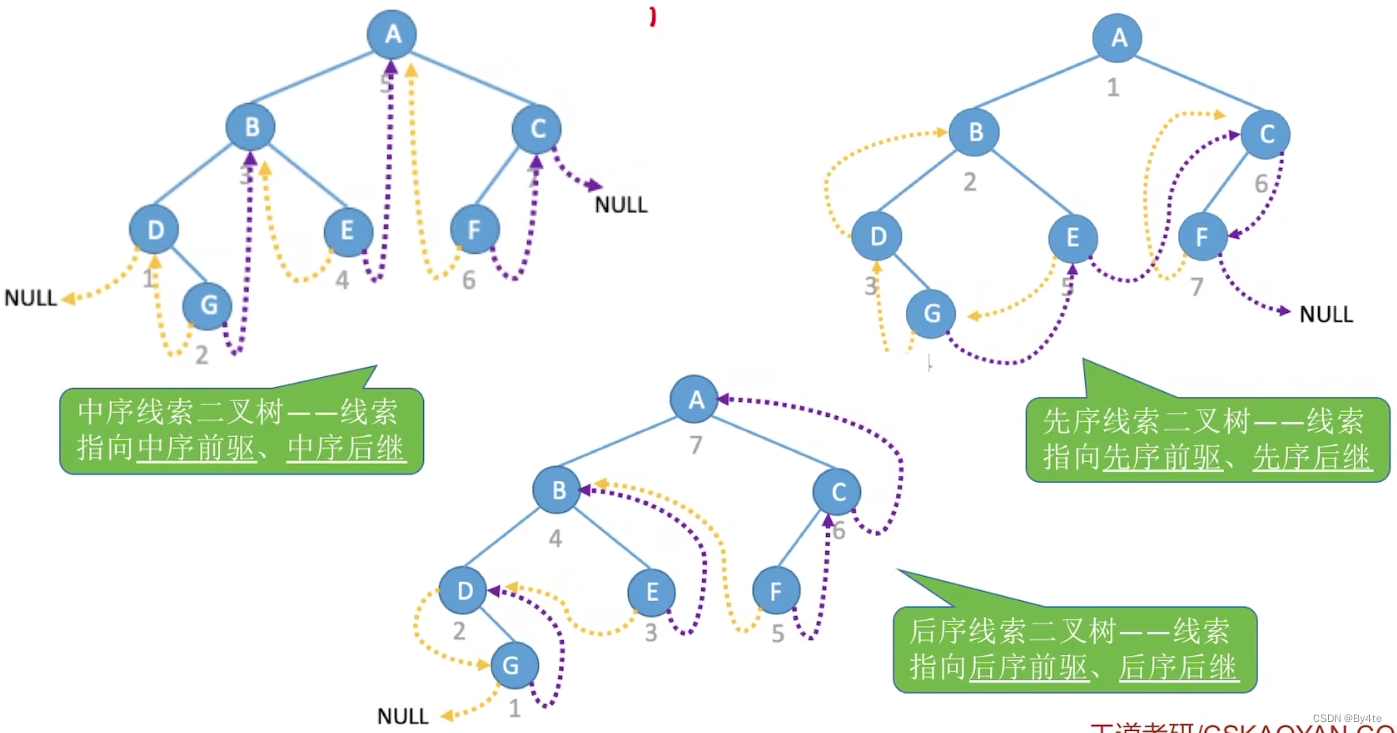
3.5 二叉树线索化

1.中序线索化

若左子树为空，建立前驱线索

2.先序线索化

3.后序线索化

3.6 线索二叉树前驱后继 

4 树和森林

4.1 树的存储结构

1.双亲表示法

顺序存储法， 每个结点中保存指向双亲的指针

2.孩子表示法

顺序+链式存储法：顺序存储每个节点，节点中保存子树链表头指针

3.孩子兄弟表示法

链式存储：保存第一个孩子和右兄弟指针

 可以完成树和二叉树的转化，森林和二叉树相互转化

4.2 树和森林的遍历

1.树的遍历

·先根遍历：若树非空，先访问根结点，再依次对每棵子树进行先根遍历

·后根遍历：若树非空，先依次对每棵子树进行后根遍历，再访问根结点

·层次遍历：①若树非空，则根节点入队；②若队列非空，队头元素出队并访问，同时将该元素的孩子依次入队；③重复②直到队列为空

2.森林遍历

·先序遍历：访问森林中第一棵树的根结点；先序遍历第一棵树中根结点的子树森林；先序遍历除去第一棵树之后剩余的树构成的森林。

·中序遍历：中序遍历森林中第一棵树的根结点的子树森林。访问第一棵树的根结点；中序遍历除去第一棵树之后剩余的树构成的森林。  

5 二叉树应用

5.1 二叉排序树

1.定义

二叉排序树又称二叉查找树（BST），其左子树结点值 < 根结点值 < 右子树结点值。使用中序遍历，可以得到一个递增的有序序列

2.查找

3.插入

4.构造

 

5.删除

6.查找效率分析

查找长度：查找运算中，需要对比关键字的次数称为查找长度，反映了查找操作时间复杂度 

平均查找长度：(层数 * 层结点数)的总和 / 总结点数

5.2 平衡二叉树

1.定义

平衡二叉树（Balanced Binary Tree)，简称平衡树（AVL树）――树上任一结点的左子树和右子树的高度之差不超过1。

结点的平衡因子 = 左子树高 - 右子树高。AVL树结点平衡因子只能是-1、0、1

2.不平衡问题调整

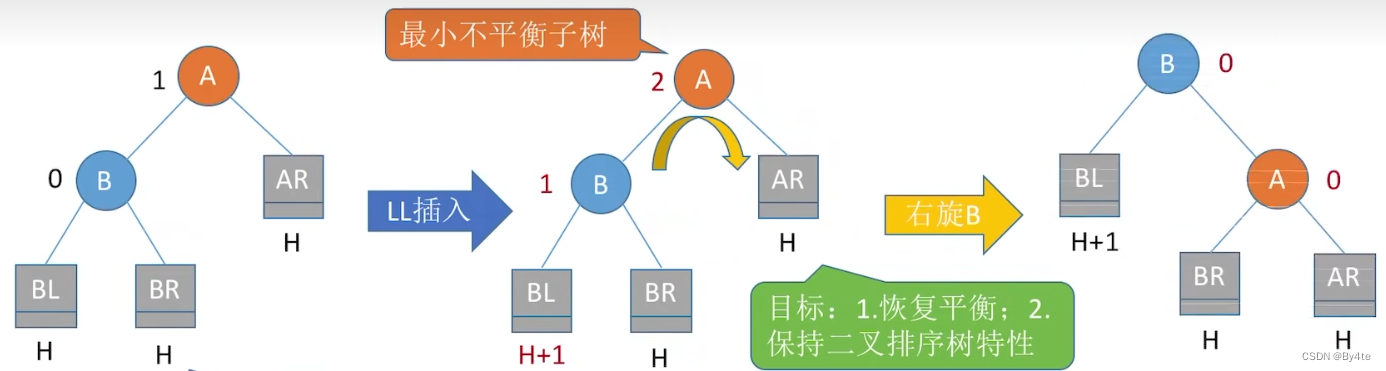
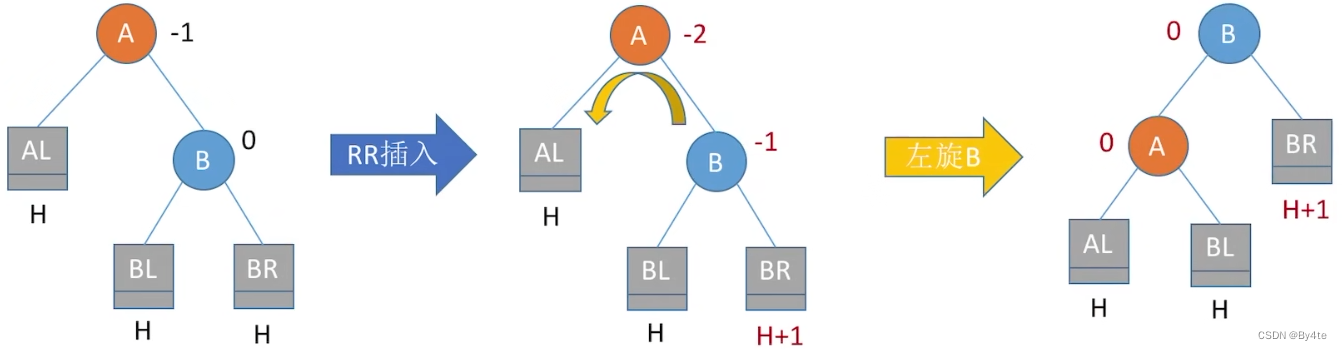
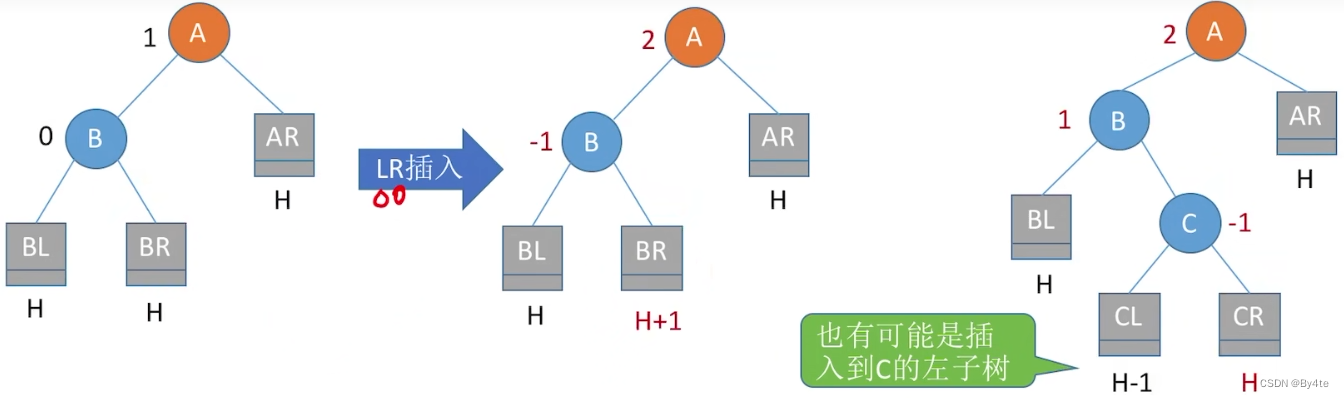
3.查找效率分析

5.3 哈夫曼树

1.带权路径长度

·结点的权:有某种现实含义的数值

·结点的带权路径长度：从树都根到该结点的路径长度与该结点上权值的乘积

·树都带权路径长度：树中所有叶结点的带权路径长度之和

2.定义

3.构造

4.哈夫曼编码

字符集中的每个字符作为一个叶子结点，每个字符出现的频度作为结点的权值，构造哈夫曼树。