单源广度优先搜索 （leetcode经典例题 C++实现）

深度优先搜索与广度优先搜索前情回顾：
深度搜索dfs与广度搜索bfs算法总结（c++ 例题）

本节是广度优先搜索的进阶：

01矩阵

传送门：
https://leetcode.cn/problems/01-matrix/?envType=study-plan&id=suan-fa-ru-men&plan=algorithms&plan_progress=1ophias

寻找数组中的每一个元素距离最近的零的距离。

利用广度优先搜索：

1. 设计一个临时的数组记录状态，我们标记每一个零。
2. 利用广度搜索把每一个零所在的坐标放入队列中，遍历队列中的每一个元素，以及其上下左右四个方向，并且依次由上一个位置的值得到当前位置的值。

我们要记录数组的每一元素距离最近的零的距离，可以发现：
0距离最近的元素就是零。
1距离最近的零可以由四周的零走一步得到，因此距离是2。

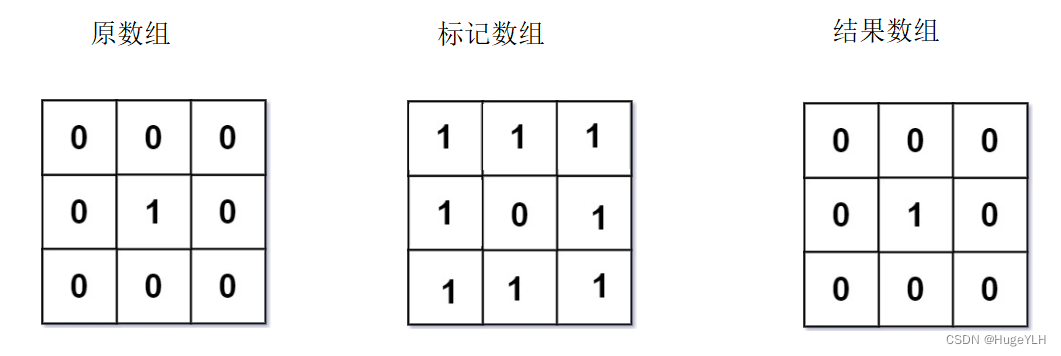
• 我们可以利用一个标记数组将初始数组中所有的0标记为1，表示我们不需要修改它的值，0的距离就是0.
• 标记数组默认初始化为0，因此所有非零元素在标记数组都被标记为0。
• 广度优先搜索遍历每一个位置，寻找标记数组中值为0的位置，这即是我们所需要修改的位置，我们可以通过它的上一步 +1 并且把这个值放到一个结果数组中，结果数组中的存储的元素即是最后的答案。
  

class Solution {
private:
    const int dirX[4]{0,0,-1,1};
    const int dirY[4]{-1,1,0,0};
public:
    vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
        int nr=mat.size(),nc=mat[0].size();
        //1. 标记数组
        vector<vector<int>> fg_mat(nr,vector<int>(nc));
        //2. 结果数组
        vector<vector<int>> dst(nr,vector<int>(nc));
        //3. 队列：广度优先搜索
        queue<pair<int,int>> q;
        //4. 预处理： 把所有的0标记为1，代表不需要管0元素的位置，但是我们要从这里开始进行广度优先搜索
        for (int i=0;i<nr;i++)
        {
            for (int j=0;j<nc;j++)
            {
                if (mat[i][j]==0)
                {
                    q.emplace(i,j);
                    fg_mat[i][j]=1;
                }
            }
        }
        //5. 开始广度搜索
        while (!q.empty())
        {
            pair<int,int> p=q.front();
            q.pop();
            //6. 遍历某个点的四个方向
            for (int i=0;i<4;i++)
            {
                int mx=p.first+dirX[i];
                int my=p.second+dirY[i];
           		//7. 只需要计算非零的元素的位置
                if (mx>=0 && mx<nr && my>=0 && my<nc && fg_mat[mx][my]==0)
                {
                	//8. 位置更新，由上一个的值 +1得到，走了一步
                    dst[mx][my]=dst[p.first][p.second]+1;
                    q.emplace(mx,my);
                    //9. 标记这个点已经走过了
                    fg_mat[mx][my]=1;
                }
            }
        }
        return dst;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

---

地图分析

传送门：
https://leetcode.cn/problems/as-far-from-land-as-possible/

地图上：0代表海洋，1代表陆地。找到海洋距离陆地最大的距离。 地图中只包含0和1两种。

这道题和上一道题基本类似：

我们寻找距离陆地最大的海洋的坐标位置，可以看作上一题：就是求距离0的最远的距离。

上一题我们已经找到了每个点距离最近的0的距离，我们只需要找到这个值最大的点，即是距离最大的点，这道题的答案。

class Solution {
private:
    const int dirX[4]{0,0,-1,1};
    const int dirY[4]{-1,1,0,0};
public:
    int maxDistance(vector<vector<int>>& grid) {
        int nr=grid.size(),nc=grid[0].size();
        //1. 标记数组
        vector<vector<int>> fg_map(nr,vector<int>(nc));
        //2. 结果数组
        vector<vector<int>> dst(nr,vector<int>(nc));
        //3. 队列
        queue<pair<int,int>> q;
        //4. 忽略陆地：把陆地视作上一题的0，我们不考虑他们，把他们标记为1，但是要从他们开始进行广度优先搜索
        for (int i=0;i<nr;i++)
        {
            for (int j=0;j<nc;j++)
            {
                if (grid[i][j]==1)
                {
                    fg_map[i][j]=1;	//注意这个位置
                    q.emplace(i,j);
                }
            }
        }
        // Step： 如果队列为空或者包含全部的数组的元素，则表示全部是海洋或者陆地，返回-1
        // (1) q.size()==0  全都是0，即全部都是海洋
        // (2) q.size()==nr*nc 全部都是1，即全部都是陆地（刚才把陆地的值入队）
        if (q.size()==0 || q.size()==nr*nc)
        {
            //全都是海洋：0 陆地：1（队列等于总大小） 
            return -1;
        }
        //5. 队列不为空：遍历所有海洋
        while (!q.empty())
        {
            pair<int,int> p=q.front();
            q.pop();
            for (int i=0;i<4;i++)
            {
                int mx=p.first+dirX[i];
                int my=p.second+dirY[i];
                //6. 遍历每一方向，广度搜索海洋距离陆地的最大距离
                if (mx>=0 && mx<nr && my>=0 && my<nc && fg_map[mx][my]==0)
                {
                	//7. 更新结果数组： 由上一步 +1得到这个点的值（即是距离）
                    dst[mx][my]=dst[p.first][p.second]+1;
                    q.emplace(mx,my);
                    //8. 标记为已经走过
                    fg_map[mx][my]=1;
                }   
            }
        }
        //9. 找到dst结果的最大值，因为我们要找到海洋距离陆地的最大距离
        int maxnum=0;
        for (auto& x:dst)
        {
            for (auto& y:x)
            {
                maxnum=max(y,maxnum);
            }
        }
        return maxnum;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

---

腐烂的橘子

传送门：
https://leetcode.cn/problems/rotting-oranges/

题目：
值 0 代表空单元格；
值 1 代表新鲜橘子；
值 2 代表腐烂的橘子。
腐烂的距离每一分钟周围的四周都会腐烂，请问当所有的橘子都腐烂，一共需要多长时间，也可能会有不会腐烂的橘子，则返回-1.

我们需要：

1. 标记数组：记录橘子的状态： 2腐烂，1正常， 0没有橘子
2. 时间数组：记录时间状态： 0零分钟 1一分钟 … -1表示如果此位置有橘子，则为正常橘子，或者它无橘子，为空。

---

1. 首先，标记数组将所有的腐烂的橘子标记为2，时间数组记录时间，如图一，这是第零分钟。
2. 第一分钟：红色为此时扩散的腐烂的橘子，表示数组更新为2（腐烂标记），时间数组更新为 1，表示第一分钟。
3. 第二分钟：蓝色为此时扩散的腐烂的橘子，表示数组更新为2，时间数组更新为 2，表示第二分钟。
4. 第三分钟：绿色为此时扩散的腐烂的橘子，表示数组更新为2，时间数组更新为 3，表示第三分钟。
5. 第四分钟：棕色为此时扩散的腐烂的橘子，表示数组更新为2，时间数组更新为 4，表示第四分钟。
6. 此时：根据标记数组可知，所有的橘子都被腐烂了，即数组中无 1 出现，此时时间数组对应的 最大值即是最后的时间 。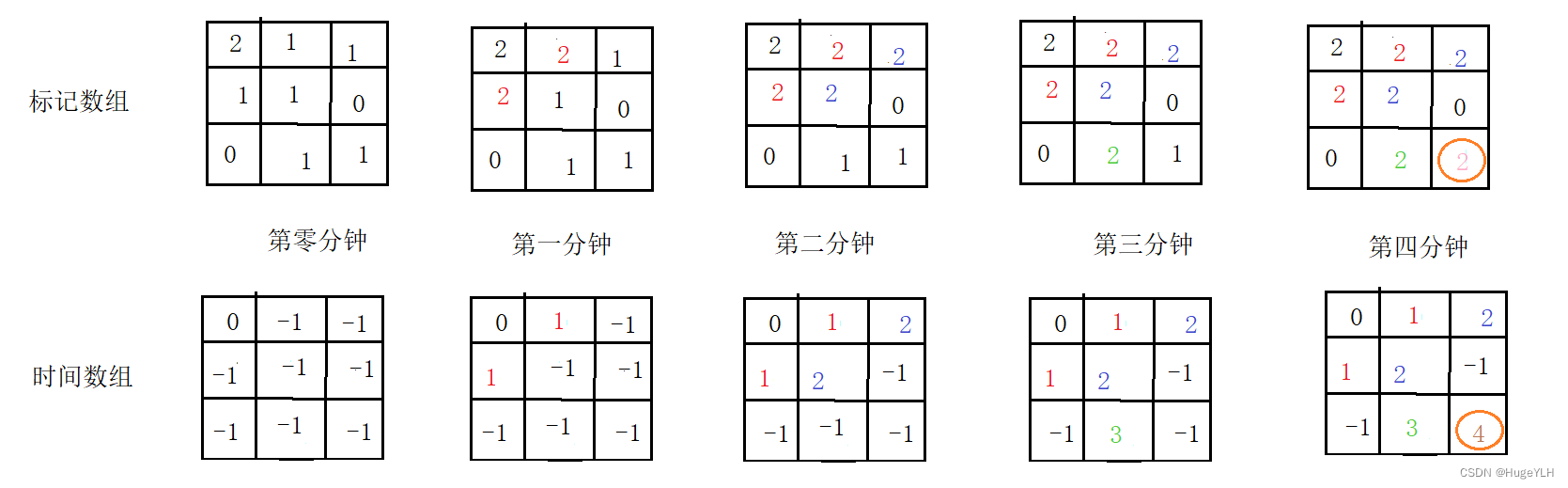
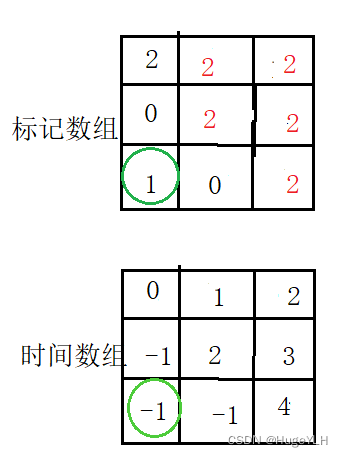
   没有腐烂的情况：

• 标记数组中出现1，正常的橘子，而且队列为空，无法继续。
• 时间数组中出现 1 ，是空或者是正常的橘子，需要对应标记数组来判断是那种情况。当然也可以直接在时间数组中再给空橘子单独设置一个值。
  

class Solution {
private:
    const int dirX[4]{0,0,-1,1};
    const int dirY[4]{-1,1,0,0};
public:
    int orangesRotting(vector<vector<int>>& grid) {
        int nr=grid.size(),nc=grid[0].size();
        vector<vector<int>> fg(nr,vector<int>(nc));
        vector<vector<int>> time(nr,vector<int>(nc));
        queue<pair<int,int>> q;
        for (int i=0;i<nr;i++)
        {
            for (int j=0;j<nc;j++)
            {
                //腐烂橘子
                if (grid[i][j]==2)
                {
                    q.emplace(i,j);
                    fg[i][j]=2;     //腐烂橘子 表示为2
                    time[i][j]=0;   //时间数组 表示为0
                }
                if (grid[i][j]==1)
                {
                    fg[i][j]=1;     //正常橘子 表示为1
                    time[i][j]=-1;  //时间数组 表示为-1
                }
            }
        }
        while (!q.empty())
        {
            pair<int,int> p=q.front();
            q.pop();
            for (int i=0;i<4;i++)
            {
                int mx=p.first+dirX[i];
                int my=p.second+dirY[i];
                if (mx>=0 && mx<nr && my>=0 && my<nc && fg[mx][my]==1)
                {
                    fg[mx][my]=2;   //橘子变腐烂
                    time[mx][my]=time[p.first][p.second]+1;  //时间增加
                    q.emplace(mx,my);  //从下一个腐烂的橘子开始
                }
            }
        }
        int max_num=0;
        for (int i=0;i<nr;i++)
        {
            for (int j=0;j<nc;j++)
            {
                max_num=max(max_num,time[i][j]);
                //时间是-1，并且表示为1，则这个橘子未腐烂，返回-1
                if (time[i][j]==-1 && fg[i][j]==1)
                {
                    return -1;
                }
            }
        }
        return max_num;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60