-
数字图像处理均衡化、规定化例题及解题思路
目录
均衡化
前置知识:
- rk:表示灰度级
- nk:表示第k个灰度级出现的个数
- sk:表示用变换函数公式计算映射后的灰度级sk
变换函数公式:
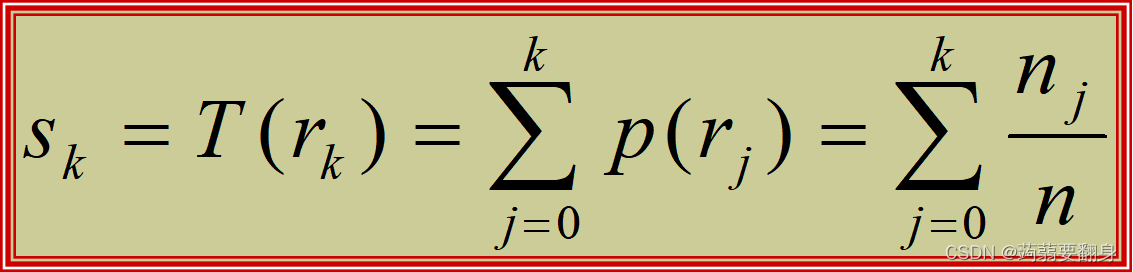
例题:
1.列表写出图像直方图均衡化的过程
2.画出均衡化以后的图像
3.画出原始图像直方图和均衡化以后的图像直方图。
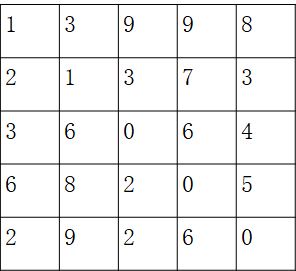
解题步骤:
①数各个灰度级的个数也就是nk
②计算概率密度,也就是pr 比如 上图中灰度级为1有2个(n1=2),所以p1=2/25=0.08
③计算sk,由步骤②得出
p0=3/25=0.12
p1=2/25=0.08
....
p9=3/25=0.12
所以
sk0=p0=0.12
sk1=p0+p1=0.12+0.08=0.20
....
sk9=p0+p1+p2+...+p8+p9=0.12+0.08+...+0.08+0.12=1
根据以上计算得出sk0≈1/9 sk1=2/9 ..... sk8≈8/9 sk9=9/9
通过sk乘以9 得出sk舍入
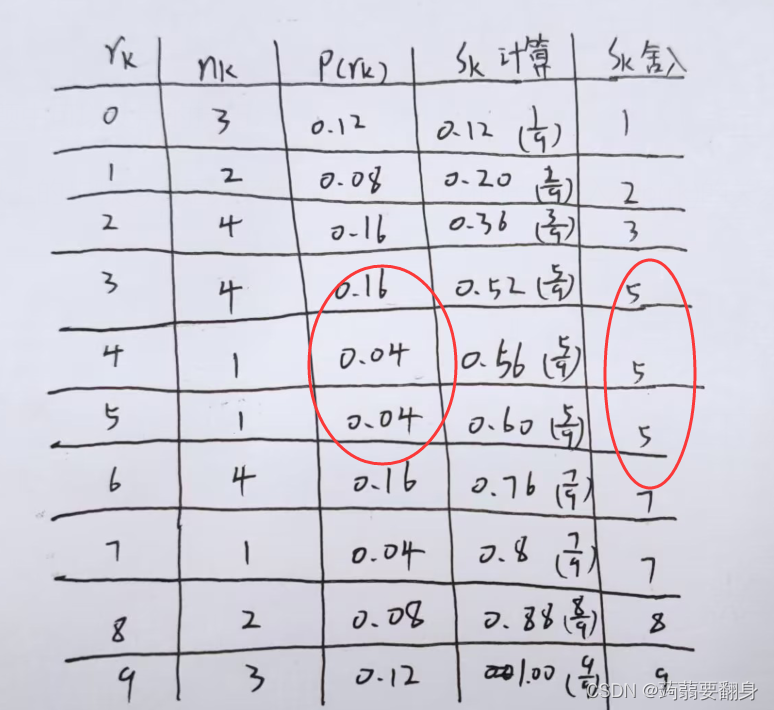
④得出表格:
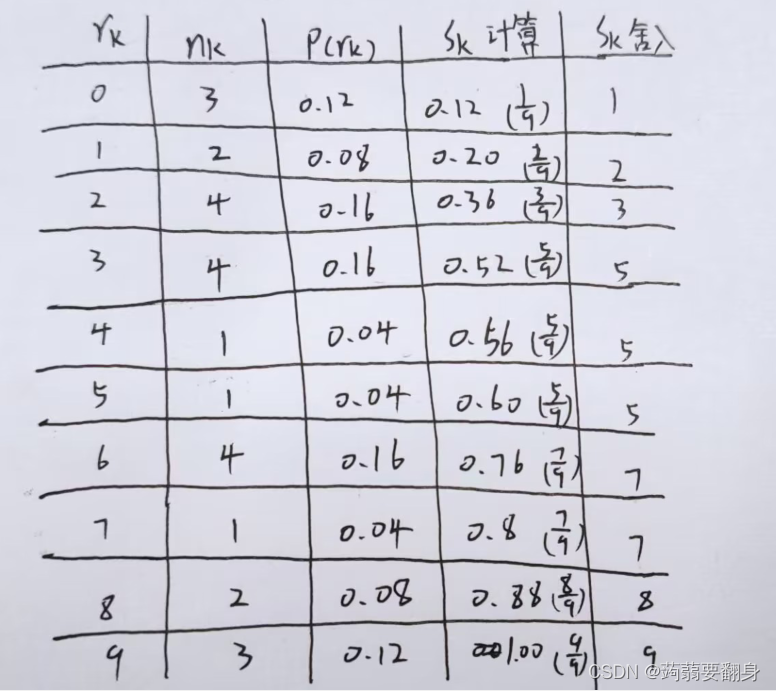
sk入rk的关系图如下:
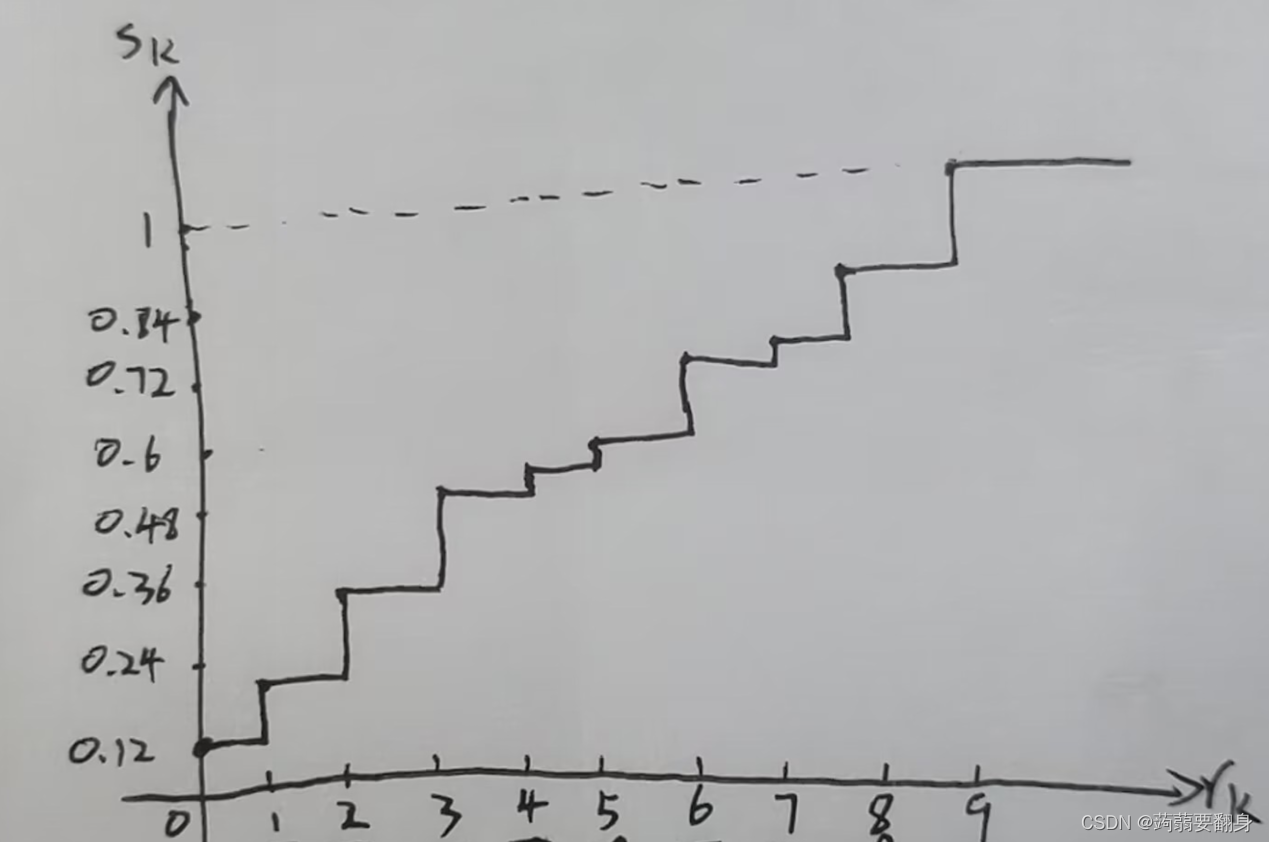
⑤根据nk 和pr画出原图像直方图
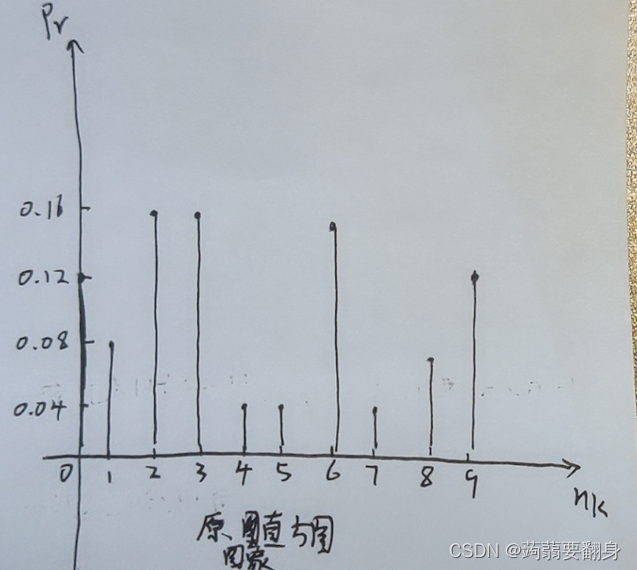
⑥根据sk舍入的值找出新的灰度级 也就是均衡化后的灰度级
技巧:看sk舍入,有几个不同就有几个新的灰度级,例如此题的有[1,2,3,5,7,8,9] 7个不同新的灰度级因此 新的灰度级为s0~s6(s0=1 s1=2 s2=3 s3=5 s4=7 s5=8 s6=9 )
⑦根据sk舍入和p(rk)的关系可以直接得出ps,例如此处的p(s3)=0.16+0.04+0.04=0.24
再例如,p(s1)=0.08,p(s0)=0.12 ,p(s6)=0.12
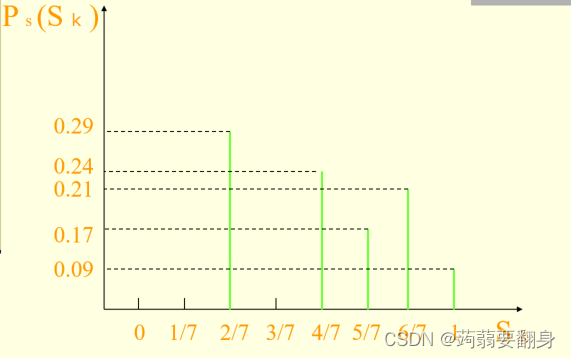
⑧画出均衡化后的直方图

⑨根据④表格中的rk 和sk舍入 画出对应其均衡化后的图像
2 5 9 9 8 3 2 5 7 5 5 7 1 7 5 7 8 3 1 5 3 9 3 7 1 注意点:
灰度级是从0开始的如果题目给你一共8个灰度级,那么sk舍入=sk计算*(灰度级-1)即sk计算*7。此题一共给出10个灰度级[0,9],因此sk舍入=sk计算乘以9(四舍五入)

其他例题:
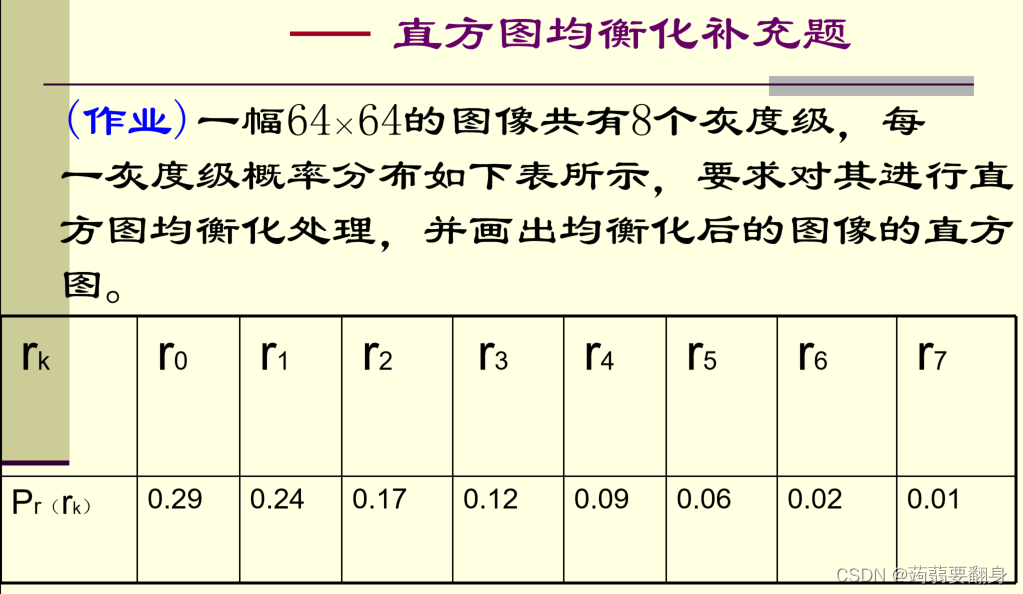
直方图均衡化的计算以及MATLAB实现 - 盐亭的森林 - 博客园
直方图均衡化——矩阵实现_Can_Yue_的博客-CSDN博客
【图像处理算法】直方图均衡化_桂哥317的博客-CSDN博客_直方图均衡化
规定化
注意:规定化是在均衡化的基础完成的,如果对均衡化理解不够,请先看上面的均衡化再来看规定化的题目。
例题与步骤:
①给出图像灰度分布表:
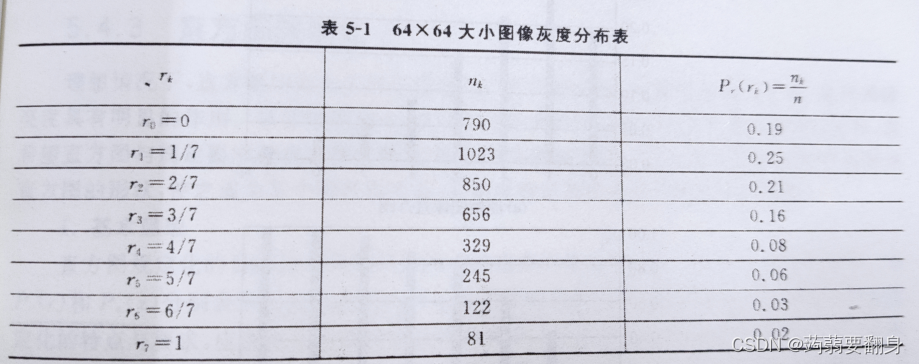
求出其均衡化后的的表格:
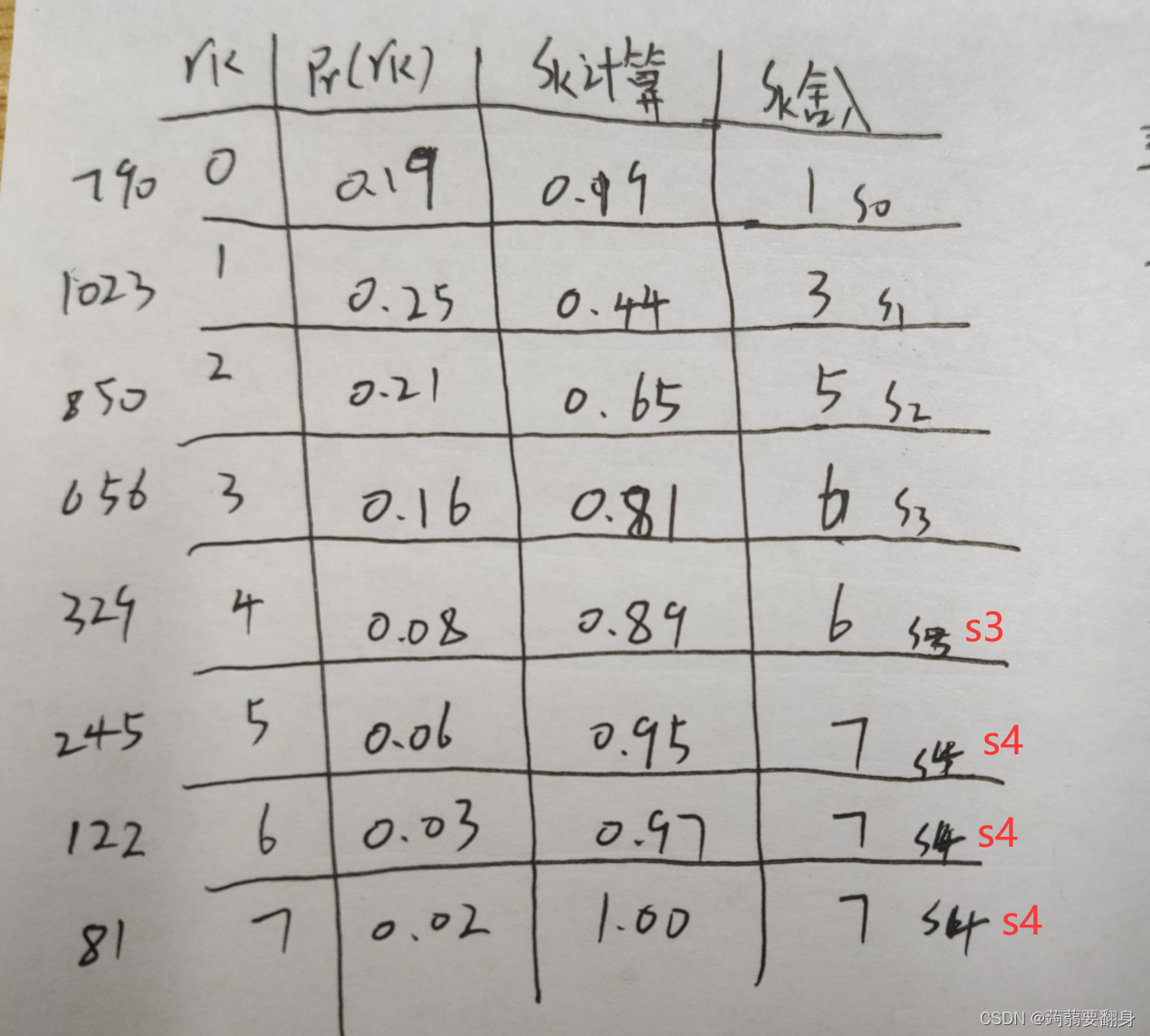
注意s0~s4是根据sk舍入的值来分配的
②给出规定化图像灰度分布表:
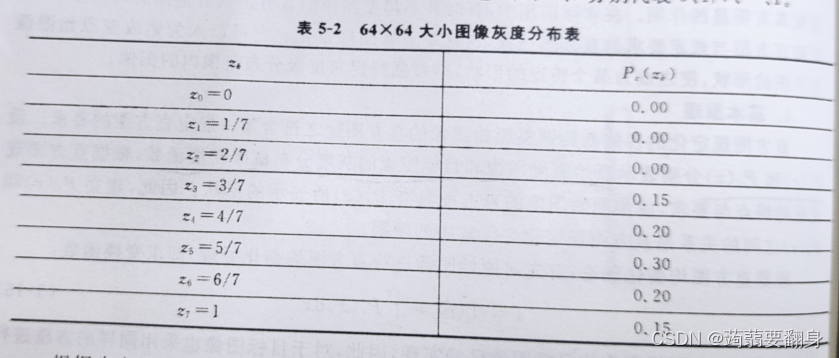
求出其均衡化后的的表格:

给下图,方便作比较:

③找出s0~s4与v0~v4 的映射关系,也就是说s0和谁最接近。例如:
s0=1,v0=1那么就说明 s0 ->v0 s0映射到v0
s1=3与v1=2最接近说明 s1 -> v1
同理 s2 - > v2 ; s3->v3 ; s4->v4
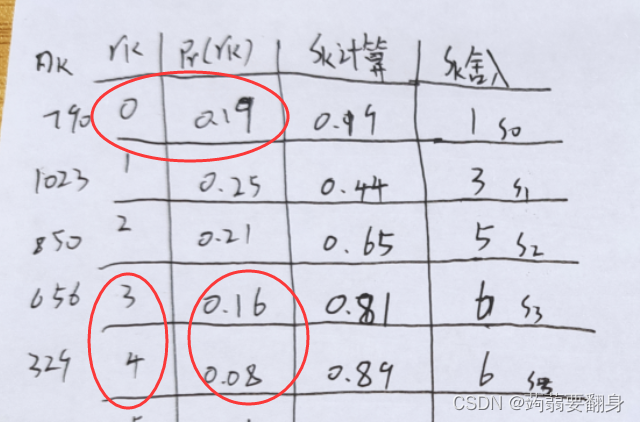
所以有这么一个关系图:(下面的图是分数,它用的是sk计算的估计值,我用的是sk舍入值)
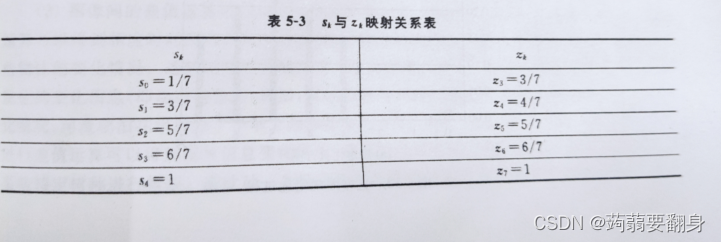
④:明白步骤③后,我们梳理一下映射关系
s0->v0 s1->v1 s2->v2 s3->v3 s4->v4
清楚之后再看看s0~s4 v0~v4都包含谁
s0: r0 s1: r1 s2: r2 s3: r3、r4 s4: r5、r6、r7
v0: z3 v1: z4 v2: z5 v3: z6 v4:z7
因此我们能够推出它们的映射关系:
r0 -> z3
r1->z4
r2->z5
r3->z6 r4->z6
r5->z7 r6->z7 r7->z7
⑤得出zk 与原直方图nk、pz(zk)的关系图
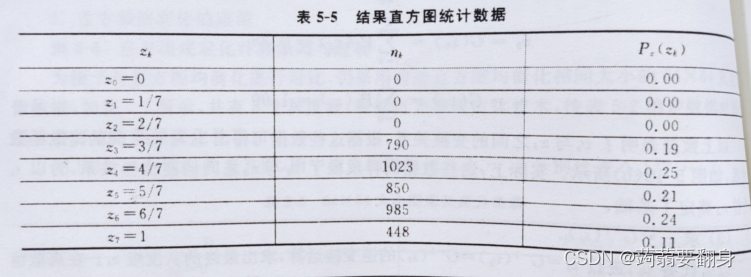
解释一下: 看z3这一行,利用映射关系知r0->z3 又因为r0的n0=790 且 p(r0)=0.19 于是得出数据
又例如:z6这一行,利用r3->z6 ,r4->z6知 r3+r4的nk为 n3+n4=656+329=985
且 p(r3)+p(r4) =0.16+0.08=0.24
⑥得出规定化直方图:(下面有参照图)
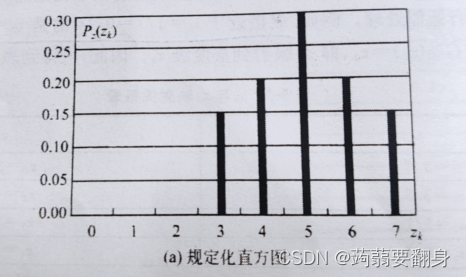
参照图:

⑦得出转换函数与直方图规定化结果:
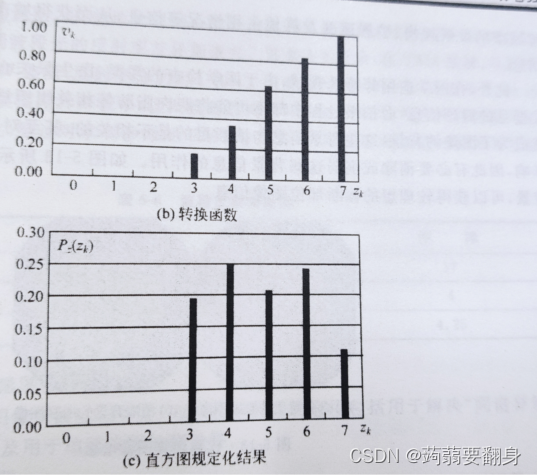
-
相关阅读:
ise使用ChipScope时报错NgdBuild:604
990-28产品经理:Different types of IT risk 不同类型的IT风险
dind(docker in docker)学习
机器学习---SVM目标函数求解,SMO算法
基于opencv+tensorflow+神经网络的智能银行卡卡号识别系统——深度学习算法应用(含python、模型源码)+数据集(三)
【搭建私人图床】使用LightPicture开源搭建图片管理系统并远程访问
JavaScript一些单行代码技巧
继承的使用以及细节问题
VC6 MFC Dialog as apllication 编程
使用项目管理系统优化公众号文章排期
- 原文地址:https://blog.csdn.net/qq_52155014/article/details/127998863