经典算法之二分法

二分法原理

我们假设一下，你的女朋友买了件衣服，告诉你衣服的价格在200~2000之间，让你猜这件衣服的价格，怎么猜才能猜的最快呢？
正确答案是：不猜，直接给女朋友转2000（手动狗头）。
错误答案是：先猜衣服的价格是：（200+2000）/2=1100，如果你的女朋友说大了。
那就猜：（200+1100）/2=650，如果这个时候说小了，那就继续猜是（650+1100）/2=875.以此类推直到猜出答案为止。为什么说这种猜法比较快呢？因为我们每次猜测后都排除掉了一半的数据。

使用条件

回想一下刚刚猜衣服价格的时候，女朋友给的条件，价格在200~2000之间。
这句话告诉了我们两个条件：
1. 价格是从有序排列的。
2. 价格是有区间范围的。

其实这就是二分法的使用条件。

使用情况

二分查找的作用当然就是查找，可是查找是需要分情况的。我们到底是查找答案本身，还是查找答案的位置呢？它们的区别又是什么呢？

二分查找位置

二分查找就是，在一个已知的有序数据上进行二分地查找，找到我们已经知道的答案（目标值）。

二分查找答案

二分答案就是，对答案可能存在的区间进行二分，对于每次的二分，要去判断此时的状态是否满足条件要求，若满足，继续向下二分，反之，向上二分，直到找出最优的答案。

两者区别

二分查找是已知答案找答案，而二分区间是已知答案区间，去找题目的最优解。

二分查找

经典题目

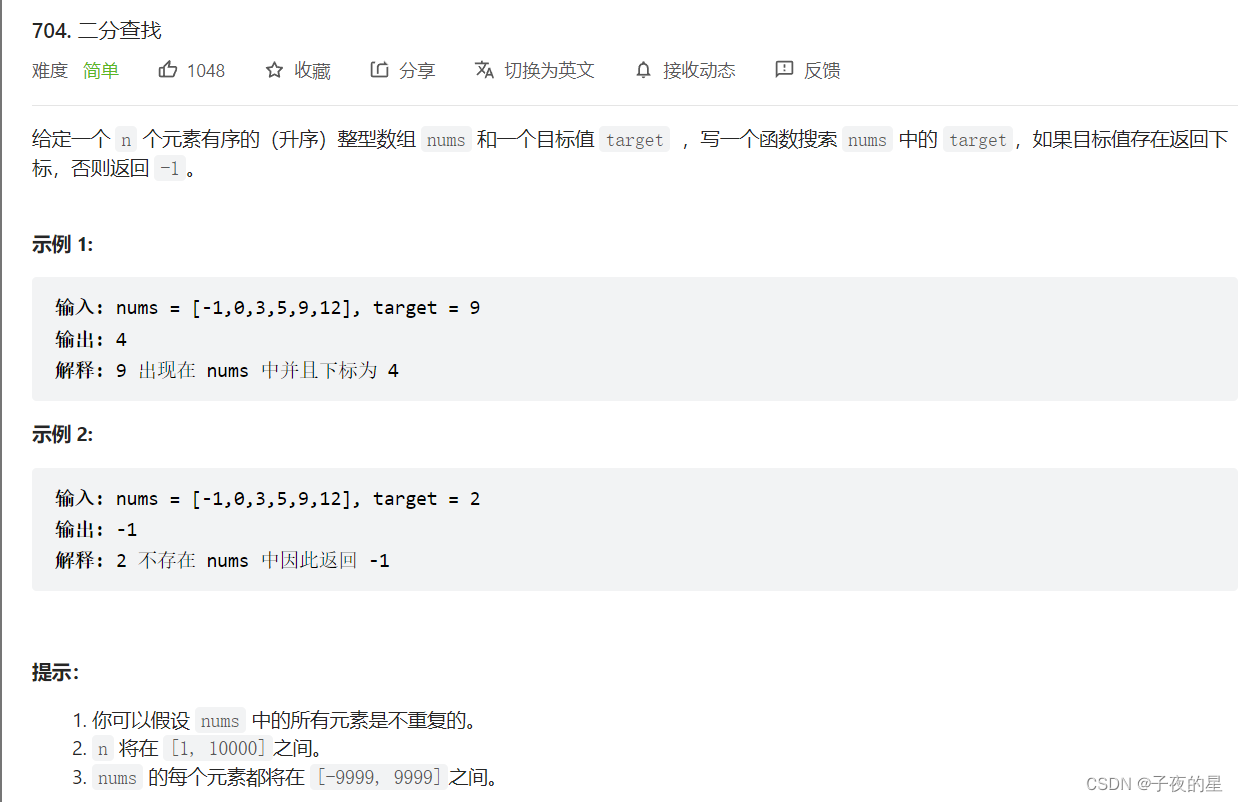
分析：首先题目告诉了我们是升序的整型数组，并且告诉了我们需要寻找的目标值。很明显是已知答案，去找答案在不在，在就返回答案数组的下标，如果不在就返回-1

int search(int* nums, int numsSize, int target)//numsSize是数组元素个数
{
    int left = 0; //left是数组第一个元素的下标
    int right = numsSize-1; //right是数组最后一个元素的下标
    while(left<=right)//循环条件是：第一个元素和最后一个元素不是一个元素。
    {
        //计算中间元素的下标
        int mid = left+right>>1;
        //如果怕数据太大导致溢出，可以写成如下形式。
        //int mid = left+(right-left>>1);
        if(nums[mid]>target) //将中间元素的值和目标值进行比较
            right = mid - 1;//缩小右区间
        else if (nums[mid]<target)
            left = mid + 1;//缩小左区间
        else //nums[mid]==target
            return mid; //返回目标数值的下标
    }
    return -1;//循环结束了还没找到。
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

二分答案

经典模板

二分答案的最大问题就是边界问题，这个也是最容易出问题的地方。
为此可以准备如下两个经典模板，以备不时之需。

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 值在右半区间： 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}

// 值在左半区间： 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

经典例题

分析：题目中的最短跳跃距离是不能超过题目所规定的范围，并且题目也把范围给出来了。也就是说，我们已经知道了答案的区间，要在这个区间里面寻找最优解。

#include
int n, m, L, d[50005];
//判断最短距离的最大值是否小于等于移动的m个石头
int check(int dis) 
{
    int count = 0, last = 0;
    for (int i = 1; i <= n; i++) 
    {
        if (d[i] - d[last] >= dis)
            last = i; //更新位置
        else 
            count++; //移走石头数加一
    }
    //不满足条件，返回0，0代表假
    if (count > m) 
        return 0;
    return 1;
}

//最优解应该在区间的左半部分

int binary_Search(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid))
            l = mid;
        else
            r = mid - 1;
    }
    return l;
}

int main() {
    scanf("%d%d%d", &L, &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d", &d[i]);
    int ret = binary_Search(1, L);
    printf("%d", ret);
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42