动态规划算法学习二：最长公共子序列

前言

一、问题描述

• 列举X的所有子序列，然后检查它是否也是Y的子序列，从而确定它是否是X和Y的公共子序列。枚举算法的时间复杂度为指数级时间复杂度。

二、DP实现

1、最优子结构性质*****

注意： 可能同时有多个长度相等的最长公共子序列！

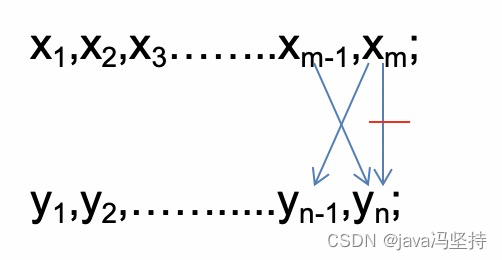
倒推—从最后一个元素开始分析

2、状态表示*****

1. 输入序列对(X_(m-1),Y_(n-1) )，(X_(m-1),Y_n ) 和(X_m,Y_(n-1) )都分别表示一个子问题 （x_m等于或不等于y_n，都可以分解为这三个子问题）

2. 子问题可以通过两个参数确定，即序列 X 的长度和序列 Y 的长度

3. C(i,j)表示序列X_i={x₁,x₂,…,x_i }和Y_j={y₁,y₂,…,y_j } 的最长公共子序列长度

4. C(m, n)则表示原问题的最长公共子序列长度

3、状态递归方程*****

• 当i=0或j=0时，C(i,j)=0；
• 当i, j>0时，C(i,j)的求解包括 两种情况 ：
  1. x_i=y_j时， (X_(i-1),Y_(j-1) )的最长公共子序列末尾添加元素x_i (=y_j)，即可得到(X_i,Y_j )的最长公共子序列
  2. x_i≠y_j时，(X_i,Y_j )的最长公共子序列等于(X_i,Y_(j-1) )和(X_(i-1),Y_j )的最长公共子序列的较大者。
     

4、计算最优值*****

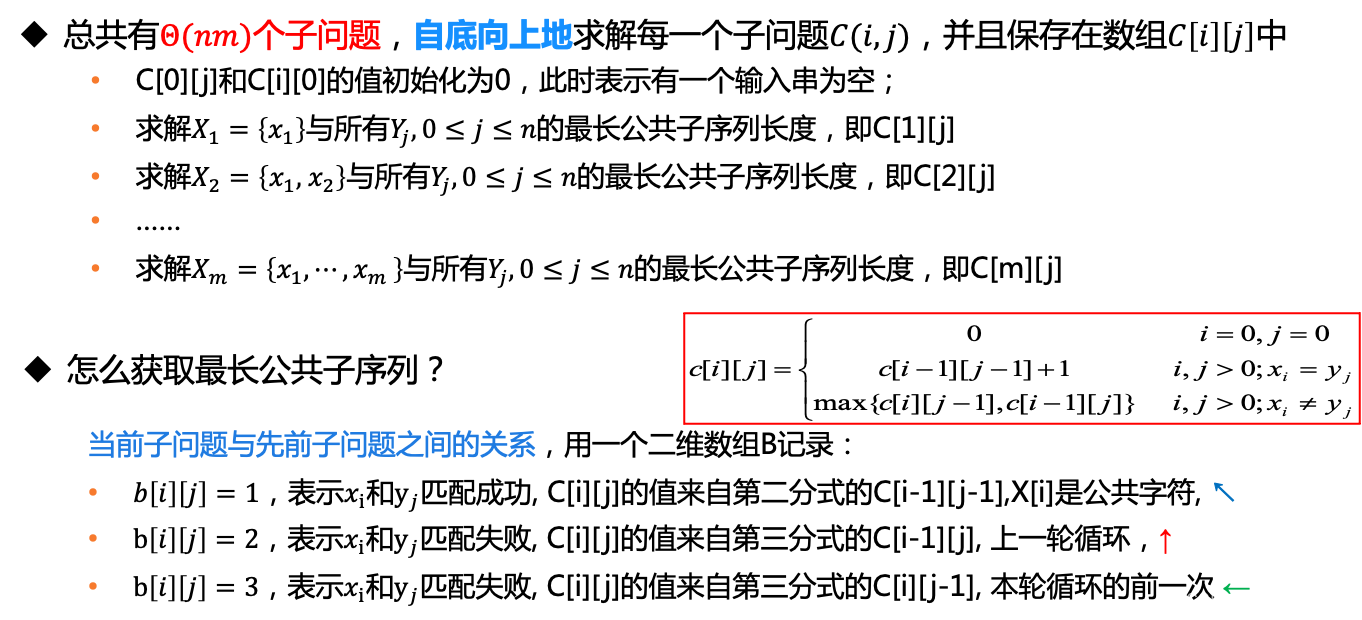
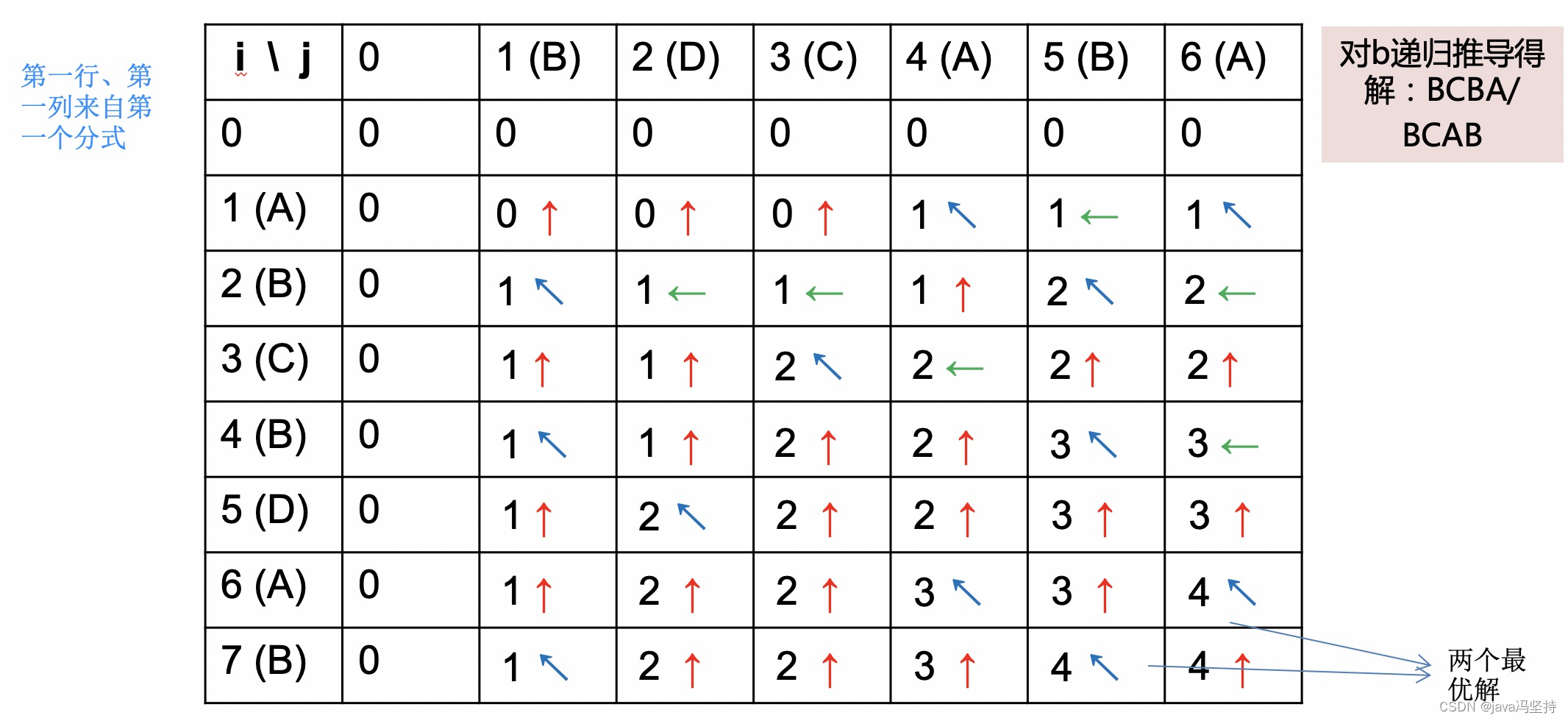
注意：
当第一次遍历 自底向上求解时，X[1] != Y[1]，所以走第三条路：求c[0][1] c[1][0]的最大值，但是这两个值都是0，所以取哪一个都可以，所以后续求最长公共子序列的 序列时，这里的左箭头和上箭头都是一样的，

1. 第一次遍历：

5、代码实现：输出最长公共子序列

代码的输出 就是最长公共子序列的长度

public class Main {
    public static int MAX = 1000;

    public static int lcsLength(char[] strX,char[] strY) {
        int[][] C = new int[MAX][MAX], B = new int[MAX][MAX];
        int i, j;

        int m = strX.length + 1;
        int n = strY.length + 1;
        for (i = 0; i < m; i++)
            C[i][0] = 0;  //初始化第一行
        for (j = 0; j < n; j++)
            C[0][j] = 0;  //初始化第一列
        for (i = 1; i < m; i++) {
            for (j = 1; j < n; j++) {
                if (strX[i-1] == strY[j-1]) {
                    C[i][j] = C[i-1][j-1] + 1;
                    B[i][j] = 1;
                } else if(C[i - 1][j] >= C[i][j - 1]) {
                    C[i][j] = C[i-1][j];
                    B[i][j] = 2;
                } else {
                    C[i][j] = C[i][j-1];
                    B[i][j] = 3;
                }
            }// end for(j
        }//end for(i
        return C[m - 1][n - 1];
    }

    public static void main(String[] args) {
        char[] x = {'A', 'B', 'C', 'B', 'D', 'A', 'B'};
        char[] y = {'B', 'D', 'C', 'A', 'B', 'A'};
        int i = lcsLength(x, y);
        System.out.println(i);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

6、代码实现：输出最优解

1