通信原理学习笔记5-2：数字调制——连续相位和恒包络问题（非线性功放、连续相位CP FSK信号、最小频移键控MSK、GMSK）

• 为了最大程度利用非线性功放，需要降低信号PAPR，这要求信号具有恒包络特性
• 信道带宽有限，需要降低信号带外泄露（进而传输失真小），要求信号具有连续相位特性（从而高频成分少）

波形连续和恒包络之间存在矛盾：想要恒包络就会有跳变（波形不连续，频谱扩展）；想要连续波信（连续相位），为了平滑过渡就没有恒包络
下面会看到：

• 错位QPSK（OQPSK）：在QPSK的基础上，基带信号的实部和虚部错位半个符号周期（成形滤波器仍然是升余弦滚降滤波器），从而改善了相位跳变
• 对于FSK，两个码元之间有相位跳变，连续相位频移键控CP FSK是一种同时满足相位连续和恒包络的调制方式
• 对于CP FSK，理论上最小的频率间隔$\Delta f=\frac{1}{2T_s}$，得到最小频移键控MSK，获得较高频谱效率
  MSK可以视为CP FSK调制指数取1/2时的特例，MSK也可以用OQPSK等价实现
• MSK的实现方法：用方波控制VCO（实现CP FSK），并且保证输出信号频率间隔为$\Delta f=\frac{1}{2T_s}$
  MSK的连续频谱仍有带外泄露问题（因为MSK不是周期信号，进而频谱也不可能在频率间隔为$\Delta f$之外突然截断，故真正的带宽大于$\Delta f$）
• 高斯滤波最小频移键控GMSK：不是直接用方波作为VCO的控制信号，而是方波先经过高斯滤波器，再作为VCO的控制信号，从而改善MSK的带外泄露问题
• 数字预失真DPD出现后，不再那么追求信号恒包络（相对而言频谱效率低），而是关注频谱效率，最终QAM技术重新胜出

非线性功放问题

功率放大器，简称功放
理想的功放能线性放大信号的功率，从而使信号传播更远，即$y(t)=kx(t)$，$k$为放大系数；
而实际中功放是非线性的

我们知道，线性系统有频率保持特性（若输入为正弦，必然输出相同频率的正弦）
而非线性系统(非线性功放)有频谱扩展问题：输入正弦，输出很多本不存在的频率成分）

为避免非线性功放的频谱扩展问题，应该尽量使用功放的线性区域（图中的$P_L$）
这就是说，需要保证功放输入端的信号最大功率不能超过$P_L$

限制输入信号最大功率为$P_L$，那么信号的峰均功率比就很重要了：$PAPR=\frac{P_{peak}}{P_{avg}}$
信号的峰均功率比PAPR越高，则信号对功放的使用效率越高（使用功放要限制输入信号最大功率，一旦输入信号PAPR较大，会导致需要进一步压低输入信号的平均功率）；

可见，为提高功放利用率，希望降低信号PAPR，特别的，具有恒包络的信号具有最低的PAPR，因此有时追求信号的恒包络特性

4QAM的恒包络特性讨论：波形连续（相位连续）和恒包络的矛盾

对于4QAM调制得到的射频信号：

• 如果成形滤波器采用矩形脉冲：射频信号恒包络，但是两个符号间有相位跳变，导致了带外泄露，频谱非常宽（引入额外高频成分）
  
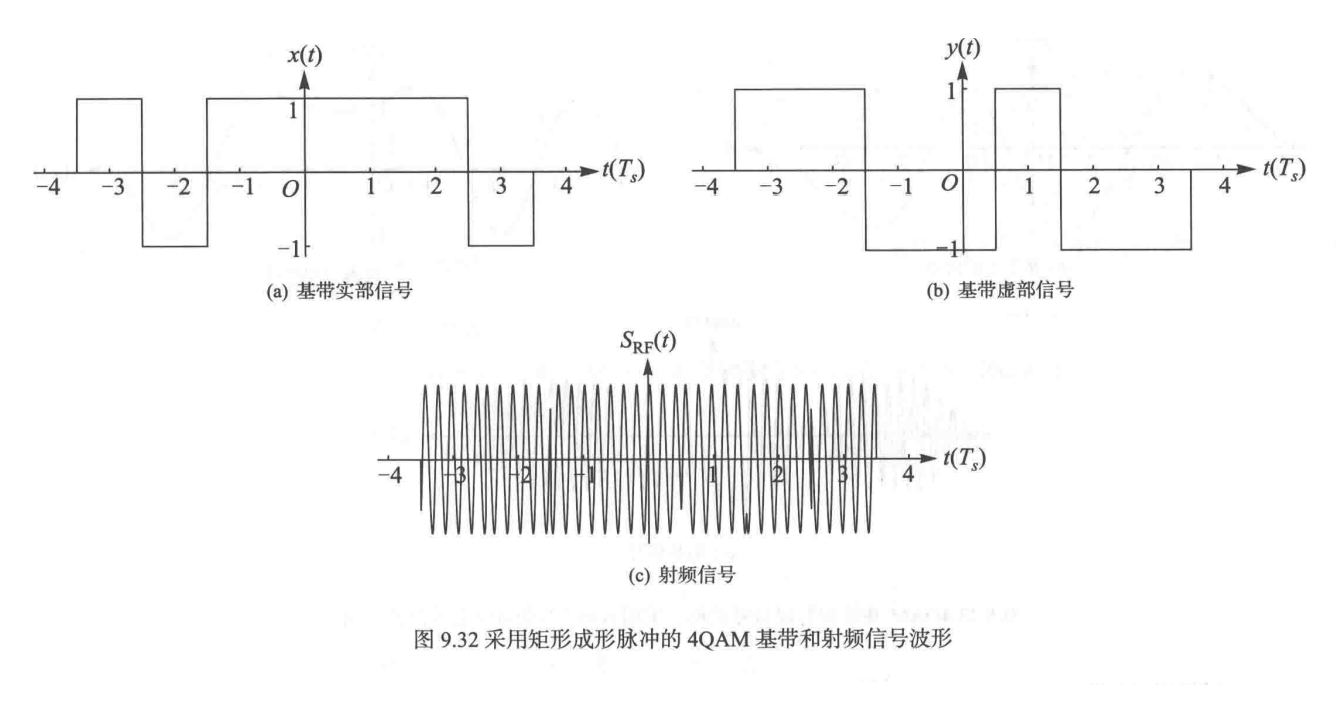
• 如果成形滤波器采用升余弦滚降滤波器：频谱限定在一定频段范围，时域波形更平滑，无相位跳变，但射频信号不再是恒包络的
  

可见对于4QAM，波形连续和恒包络之间存在矛盾：想要恒包络就会有跳变（波形不连续，频谱扩展）；想要连续波信（连续相位），为了平滑过渡就没有恒包络

是否存在同时满足相位连续和恒包络的调制方式呢？这就是下面将介绍的连续相位频移键控CP FSK

连续相位频移键控CP FSK

连续相位频移键控CP FSK（Continuous Phase FSK）原理很简单：用（矩形的）基带脉冲信号控制压控振荡器VCO，从而频率被调制了的FSK信号
注意，VCO的输出信号为：$$\begin{gathered} s_{\mathrm{R}\mathrm{F}}(t)=\cos [\theta (t)]， \\ \begin{array}{rl}其中信号的总相位\theta (t)& =2\pi f_{c}t+\hat{\varphi }(t)\\ & =2\pi f_{c}t+K{\int }_{-\infty }^t{u}_c(\tau )\\ & =2\pi f_{c}t+2\pi h{\int }_{-\infty }^t{u}_c(\tau )\end{array} \end{gathered}$$

• 输出信号的频率：$\omega (t)=\frac{\mathrm{d}}{\mathrm{d}t}\theta (t)=2\pi f_c+K{u}_c(t)$，也就是说输出信号的瞬时角频率由输入$u_c(t)$线性控制，实现了FSK
• 输出信号的相位：$\theta (t)=K{\int }_{-\infty }^t{u}_c(\tau )$，由于积分的作用，无论$u_c(t)$波形如何（即使为跳变的方波），输出信号相位必然连续

其中，从输入信号$u_c(t)$和输出信号频率是线性关系，只相差一个系数$K$

• $K$是VCO的灵敏度系数$K=4\pi f_d{T}_s$
  其中$f_d$为最大频率偏移（它是FSK的带通信号频谱带宽的一半，即频谱最边缘部分相对于中心频率的偏移）
• 对于CP FSK，我们定义一个参数：调制系数（modulation index）$h=2f_d{T}_s$；
• 灵敏度系数和调制系数的关系：$K=4\pi f_d{T}_s=2\pi h$

例如，用矩形的基带脉冲作为VCO的控制信号$u_c(\tau )$，输出的CP FSK信号如下

如果信息比特经过矩形脉冲$g(t)$进行脉冲成形，则上式中基带信号（VCO控制电压）$u_c(t)={\sum }_n{I}_{n}g\left(\tau -n{T}_s\right)$，则有CP FSK信号：$$s_{\mathrm{R}\mathrm{F}}(t)=\cos \left[2\pi f_{c}t+K{\int }_{-\infty }^t{u}_c(\tau )\mathrm{d}\tau \right]=\cos \left[2\pi f_{c}t+2\pi h{\int }_{-\infty }^t\sum _n{I}_{n}g\left(\tau -n{T}_s\right)\mathrm{d}\tau \right]$$CP FSK信号波形如图：

与之对比，普通的FSK（非连续相位FSK）则在两个符号之间有跳变，频谱出现高频成分，即带外泄露

最小频移键控MSK

对于FSK而言，不同符号可以对应不同的频率，并且频率间隔越小，能够实现的频谱效率越高；

• 然而FSK的频率间隔不能无限小，下面将证明，实现正交的两个余弦信号，其频率间隔最小为$\Delta f=\frac{1}{2T_s}$（注意，不是$\frac{1}{T_s}$，而是最小可以做到其一半）
• 最小频移键控MSK：使用了（理论上最小的）频率间隔$\Delta f=\frac{1}{2T_s}$的FSK
• 若考虑2FSK，显然仅有的两个频率就在中心频率的两侧，故有频率间隔$\Delta f=2f_d$（两倍最大频率偏移）
  结合上面的CP FSK的调制指数概念，从而有：MSK的调制指数为1/2（$h=2f_d{T}_s=\Delta f{T}_s=\frac{1}{2T_s}{T}_s=\frac{1}{2}$）

MSK可以视为CP FSK的特例：CP FSK采用的频率间隔为（理论上最小的）$\Delta f=\frac{1}{2T_s}$即为MSK，或者说CP FSK的VCO的灵敏度取$K=\pi$、调制指数取$h=1/2$即为MSK

证明：实现正交的两个余弦信号，其频率间隔最小为$\Delta f=\frac{1}{2T_s}$
将两个FSK已调信号（不同频率的余弦信号）做内积，若结果为0则两者正交，说明可以区分出这两个频率成分
$$\begin{array}{rl}{\rho }_{km}& =⟨\Re \left[s_m(t)\right],\Re \left[s_k(t)\right]⟩\\ & ={\int }_0^{T_s}\cos (2\pi k\Delta ft)\cos (2\pi m\Delta ft)\mathrm{d}t\\ & =\frac{1}{2}{\int }_0^{T_s}\cos [2\pi (m-k)\Delta ft]+\cos [2\pi (m+k)\Delta ft]\mathrm{d}t\\ & =\frac{1}{2}\left(\frac{\sin \left[2\pi (m-k)\Delta f{T}_s\right]}{2\pi (m-k)\Delta f}+\frac{\sin \left[2\pi (m+k)\Delta f{T}_s\right]}{2\pi (m+k)\Delta f}\right)\end{array}$$上式中，要使得两个相邻频率（$m-k=1$）的余弦信号正交，即${\rho }_{km}=0$，要求$\Delta f=\frac{n}{2T_s}$（其中$n$为任意正整数），进而最小频率间隔就是$\Delta f=\frac{1}{2T_s}$

例如，给定了符号周期$T_s$，满足$\Delta f=\frac{1}{2T_s}$的互相正交的余弦信号如下（$m=0\sim 4$）

高斯滤波最小频移键控GMSK

MSK的实现：用方波控制VCO，并且保证输出信号频率间隔为$\Delta f=\frac{1}{2T_s}$

然而这样做仍不完美：虽然VCO输出信号相位连续，且频率间隔最小，但是MSK的连续频谱仍有带外泄露问题（MSK不是周期信号，不可能只有两根谱线，频谱也不可能在频率间隔为$\Delta f$之外突然截断，因此真正的带宽大于$\Delta f$）

• 高斯滤波最小频移键控GMSK：不是直接用方波作为VCO的控制信号，而是方波先经过高斯滤波器，再作为VCO的控制信号
  这样，高斯滤波器减小了VCO控制电压的高频成分，从而改善了MSK的带外泄露问题

高斯滤波器：$$h(t)=K{\mathrm{e}}^{-\frac{t^2}{2{\sigma }^2}},H(\omega )=K\sigma {\mathrm{e}}^{\frac{{\omega }^2}{2/{\sigma }^2}}$$
其中，高斯滤波器的带宽由参数$\sigma$决定，$\sigma$越大带宽越小；
实际中常用的高斯滤波器的指标是$B{T}_s$，其中$B$是高斯滤波器的-3dB带宽
GSM中，就采用了$B{T}_s=0.3$的GMSK调制

• MSK方案下，使用矩阵脉冲$Rect(t)$进行脉冲成形，得到的基带波形作为VCO控制信号：$u_c(t)={\sum }_n{I}_n\mathrm{Rect}\left(t-n{T}_s\right)$
• GMSK带来了更好的频谱特性（带外泄露少），与此同时误码率增高，需要综合考虑与权衡这对矛盾

GMSK方案与MSK方案的联系：
理解1：先将原始MSK基带波形 与 高斯滤波器求卷积，再将卷积作为VCO控制信号：$$u_c(t)=\sum I_n\mathrm{Rect}\left(t-n{T}_s\right)\ast h(t)=\sum _n{I}_{n}g\left(t-n{T}_s\right)$$
理解2：MSK使用的成形滤波器是$Rect(t)$，而GMSK使用的成形滤波器是$g(t)=\mathrm{Rect}(t)\ast h(t)$

由于GMSK的成形滤波器$g(t)$不满足Nyquist准则，引入码间串扰，从而GMSK误码性能比MSK稍差

MSK的OQPSK等效实现

• 错位QPSK（OQPSK）：在QPSK的基础上，基带信号的实部和虚部错位半个符号周期（成形滤波器仍然是升余弦滚降滤波器）
• 错位的好处是：相邻两个码元对应的星座点 一定是邻近的（或者就是同一个），对应的相位跳变至多为90度（而普通QPSK最大相位跳变为180度）
  或者从IQ两路信号合成的角度来看，OQPSK避免了实部和虚部同时过零点的情况，从而防止已调信号出现幅度很小的包络（如图中$-1.5T_s$处），从而PAPR特性更好，有利于高效使用非线性功放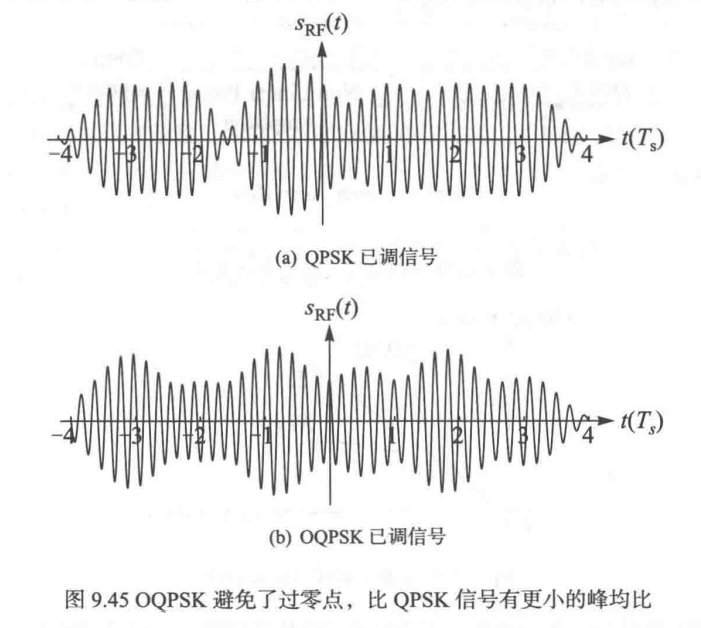

上面的OQPSK，使用升余弦滚降滤波器来进行脉冲成形，然而信号并非恒包络；
如果成形滤波器换为一个特殊的半正弦成形函数，则此时OQPSK等价于MSK。
下图中，实线对应半正弦成形函数，虚线对应升余弦滚降滤波器

实际上，通过推导带通MSK信号的等效复基带信号，会发现MSK就是 实部发送偶数消息、虚部发送奇数消息、使用半正弦成形脉冲$g(t)$的QPSK
s M S K = A { [ ∑ n I 2 n g ( t − 2 n T ) ] c o s ( 2 π f c t ) + [ ∑ n I 2 n + 1 g ( t − 2 n T − T ) ] s i n ( 2 π f c t ) } s_{MSK} = A\{ [\sum_{n}I_{2n}g(t-2nT)] cos(2\pi f_c t)+[\sum_{n}I_{2n+1}g(t-2nT-T)] sin(2\pi f_c t)\} sMSK​=A{[n∑​I2n​g(t−2nT)]cos(2πfc​t)+[n∑​I2n+1​g(t−2nT−T)]sin(2πfc​t)}
其中，由于每个码元周期 要么I路固定而Q路发送新的$I_{2n+1}$，要么Q路固定而I路发送新的$I_{2n}$，这显然与OQPSK的特性一致，因此最终可以用OQPSK来等价实现MSK（但是注意，基带脉冲成形必须使用半正弦脉冲才能得到MSK，不能使用普通OQPSK的升余弦脉冲）

• 总结：使用半正弦成形的OQPSK，等价于MSK调制
  

线性功放与QAM的重新崛起

GMSK在2G的GSM中获得应用，然而在3G和4G中又是PSK和QAM一统江山，这与线性功放技术有关

• 线性功放技术：核心就是数字预失真DPD（Digital Pre-Distortion）
  数字预失真DPD就是对非线性功放的“逆向还原”，最终整个功放表现为线性的，DPD大幅扩大了功放的线性范围，在3G后的系统中广泛应用
  

• 产生线性功放技术后，由于功放的线性范围扩大，对信号的PAPR指标要求没有GSM中那么严格，也就是说不再一味的追求信号的恒包络

• （毕竟恒包络也有代价：一方面OQPSK中的半正弦成形滤波不是严格带限的，造成带外泄露；另一方面恒包络意味着无法通过幅度传递信息，上述的CP FSK、OQPSK等技术调制结束都不高（每个码元承载比特信息少），频谱效率低，然而4G更追求频谱效率）

• 最终QAM（包括QPSK）在3G和4G中胜出

有意思的是，Offset QAM技术并未胜出
虽然Offset QAM相对于QAM有一定优势，即可以如OQPSK那样避免零包络，从而降低PAPR；
然而Offset QAM的优势不明显，尤其是16QAM以上时信号零包络概率很小，还引入一定复杂度；
而QAM简单、没有明显技术劣势，从而胜出