883. 三维形体投影面积

883. 三维形体投影面积

在 n x n 的网格 grid 中，我们放置了一些与 x，y，z 三轴对齐的 1 x 1 x 1 立方体。

每个值 v = grid[i][j] 表示 v 个正方体叠放在单元格 (i, j) 上。

现在，我们查看这些立方体在 xy 、yz 和 zx 平面上的投影。

投影 就像影子，将 三维 形体映射到一个 二维 平面上。从顶部、前面和侧面看立方体时，我们会看到“影子”。

返回 所有三个投影的总面积 。

示例 1：

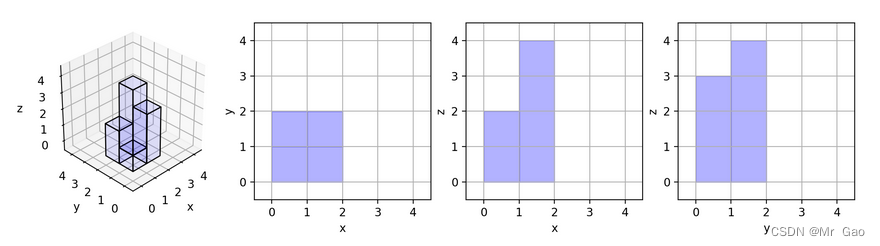
输入：[[1,2],[3,4]]
输出：17
解释：这里有该形体在三个轴对齐平面上的三个投影(“阴影部分”)。

示例 2:

输入：grid = [[2]]
输出：5

示例 3：

输入：[[1,0],[0,2]]
输出：8

个人觉得这题也算是很有趣的一个题目吧，解题代码如下：

int projectionArea(int** grid, int gridSize, int* gridColSize){
    int re=0;
    for(int i=0;i<gridSize;i++){
        int max=grid[i][0];
         for(int j=0;j<gridColSize[0];j++){
          if(grid[i][j]!=0){
             re++;
         }
             max=fmax(max,grid[i][j]);
        

         }
         
         re=re+max;
        
    }
    for(int i=0;i<gridSize;i++){
        int max=grid[0][i];
         for(int j=1;j<gridColSize[0];j++){
             max=fmax(max,grid[j][i]);
        

         }
        
         re=re+max;
    }
 
    return re;

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30