如何处理海量数据文件以及大文件数据查找

目录

一.处理海量整数文件

①问：假定有40亿个无符号整数，判断某数据是否在其中？

②问：假定有40亿个无符号整数，找到只出现一次的数据，两次，三次...？

③问：两个文件各有100亿个整数，只有1G内存，找交集整数？

二.处理海量数据（非整数）文件

①问：超过100G大小的日志文件，存放的都是IP地址，求其中出现次数最多的IP地址？

求Top K个地址？

②问：两个文件分别有100亿个字符串，内存大小为1G，求交集字符串？（精确和近似）

---

一.处理海量整数文件

①问：假定有40亿个无符号整数，判断某数据是否在其中？

如果是使用遍历的思想 ，那么时间复杂度为O(n)。

就算数据已经排好序，使用二分查找时间复杂度也有O(log^n)。

不管是哪种，面对40亿个数据其效率都不会太高。

这时，使用位图+哈希思想解决就很重要。因为是无符号整数，正好一个数映射一个比特位（相当于直接定址法），而且不会出现哈希冲突。

当找寻数据时，只需要在位图中找到该整数对应的比特位，如果为1说明有，0说明没有。

当然，前提是整数进文件时就已经建立位图了，否则查找时再建立位图还是要遍历文件。 

如果是40亿个整数，最多就需要40亿个比特位，即476MB。换句话说就是利用空间换时间。

②问：假定有40亿个无符号整数，找到只出现一次的数据，两次，三次...？

这时一个位图已经无法满足需求，因为一个位图只能通过0和1判断数据是否存在。

那么使用两个位图呢？

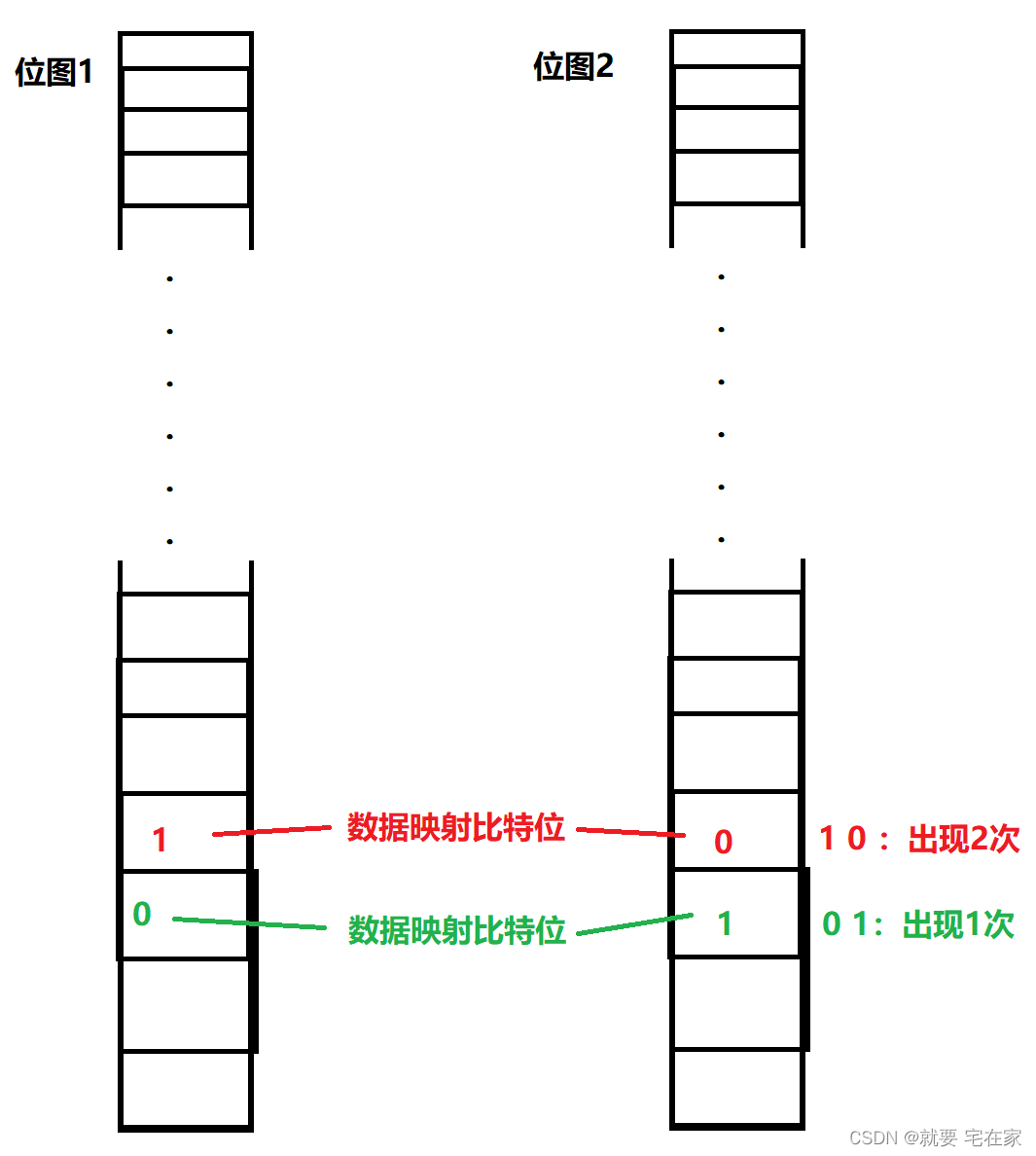
同样，一个整数只会映射一个比特位，在两个位图中会映射同样的比特位，这两个比特位正好可以用于记录数据出现的次数。同样的整数第一次映射时置为0 1，第二次为1 0，第三次为1 1。

此时两个位图最多判断出现3次的整数，如果需要找到出现更多次的使用更多的位图即可。

图例如下：

③问：两个文件各有100亿个整数，只有1G内存，找交集整数？

虽然各有100亿个整数，但是int取值最大范围为正负21亿左右，共有约42亿个数据。

因此，这个问题还是使用位图+哈希来解决。

先取一个文件全部整数进行哈希映射，之后另一个文件在哈希映射中找比特位为1的即可。

二.处理海量数据（非整数）文件

①问：超过100G大小的日志文件，存放的都是IP地址，求其中出现次数最多的IP地址？

求Top K个地址？

数据是日志非整数，所以已经无法通过位图直接解决。同时数据过大，内存中显然无法直接装下。

这时，我们应该通过使用哈希切分思想来解决这个问题。

首先把文件分成足够多的小份，每一小份都应该是内存能直接处理的大小，且小文件数量要合理。如果数量过少，那么数据分配不平均，如果数量过多，会造成资源浪费。

我们假设分成1000份。

之后把大文件中数据通过哈希函数映射到相应的小文件中。因为同样的数据映射的是同一份小文件。因此所有相同的数据一定在同一份文件中。

之后在内存中找到小文件中出现次数最多的数据。再将这个数据与其他小文件中次数最多的数据比较，找到整个大文件中出现次数最多的数据。

对于Top K问题，将每份小文件中出现次数最多的数据建立一个最小堆即可。

图例如下：

 

②问：两个文件分别有100亿个字符串，内存大小为1G，求交集字符串？（精确和近似）

 精确算法：按照哈希切分思想即可，将两个文件数据通过哈希映射分成内存能处理的小份文件。再将两个文件中同样编号的小文件进行对比即可。

图示如下：

近似算法：用一份文件数据建立布隆过滤器，之后另一份文件数据再通过该布隆过滤器进行判断即可。

因为布隆过滤器的特性，判断存在的可能存在，判断不存在的一定不存在。

与精确算法相比，近似算法空间消耗更低，但存在误判率。

编译器永远比你懂微观优化，只能向它不擅长的方向努力——未名 

---

如有错误，敬请斧正