2415. 反转二叉树的奇数层-层次遍历

2415. 反转二叉树的奇数层-层次遍历

给你一棵 完美 二叉树的根节点 root ，请你反转这棵树中每个 奇数 层的节点值。

例如，假设第 3 层的节点值是 [2,1,3,4,7,11,29,18] ，那么反转后它应该变成 [18,29,11,7,4,3,1,2] 。
1

反转后，返回树的根节点。

完美 二叉树需满足：二叉树的所有父节点都有两个子节点，且所有叶子节点都在同一层。

节点的 层数 等于该节点到根节点之间的边数。

示例 1：

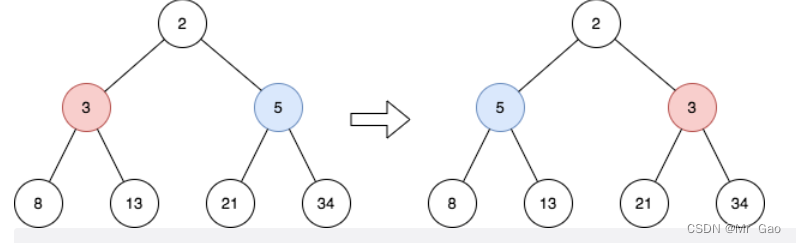
输入：root = [2,3,5,8,13,21,34]
输出：[2,5,3,8,13,21,34]
解释：
这棵树只有一个奇数层。
在第 1 层的节点分别是 3、5 ，反转后为 5、3 。

示例 2：

输入：root = [7,13,11]
输出：[7,11,13]
解释：
在第 1 层的节点分别是 13、11 ，反转后为 11、13 。

示例 3：

输入：root = [0,1,2,0,0,0,0,1,1,1,1,2,2,2,2]
输出：[0,2,1,0,0,0,0,2,2,2,2,1,1,1,1]
解释：奇数层由非零值组成。
在第 1 层的节点分别是 1、2 ，反转后为 2、1 。
在第 3 层的节点分别是 1、1、1、1、2、2、2、2 ，反转后为 2、2、2、2、1、1、1、1 。

解题代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
#define size 10000

struct TreeNode* reverseOddLevels(struct TreeNode* root){
    int val;
    struct TreeNode *queue[size];
    int rear=0,front=0;
    queue[rear++]=root;
    int t[20000];
    int sizet=0;

    while(front!=rear){
        struct TreeNode* p=queue[front];
       
        t[sizet++]=p->val;
        front=(front+1)%size;
        if(p->left){
             queue[rear]=p->left;
            rear=(rear+1)%size;

        }
         if(p->right){
             queue[rear]=p->right;
            rear=(rear+1)%size;

        }

    }
   
    int p=0;
    int sizep=2;
    printf("sizet %d ",sizet);
    for(int j=1;j<sizet;j=j+p*2+p*4){
        if(j>sizet){
            break;
        }
       
        if(j+sizep>=sizet){
            sizep=sizet-j;

        }
        

        for(int k=0;k<sizep/2;k++){
           // printf("%d %d ", t[j+k],[j+sizep-k-1]);
            int z=t[j+k];
            t[j+k]=t[j+sizep-k-1];
            t[j+sizep-k-1]=z;

        }
          if(j+sizep>=sizet){
           break;

        }
        sizep=sizep*4;
        if(p==0){
            p=1;
        }
        else{
            p=p*4;
        }

      
        

    }
   
    rear=0,front=0;
    sizet=0;
    queue[rear++]=root;
    while(front!=rear){
        struct TreeNode* p=queue[front];
       
        p->val=t[sizet++];
        front=(front+1)%size;
        if(p->left){
             queue[rear]=p->left;
            rear=(rear+1)%size;

        }
         if(p->right){
             queue[rear]=p->right;
            rear=(rear+1)%size;

        }

    }
  
    return root;
    

   

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101