Python常见操作的时间复杂度

本文整理了Python中常见数据结构操作的时间复杂度，旨在帮助大家了解Python操作的性能，协助大家写出更快的代码。

程序时间复杂度一般用"大O表示法（Big-O notation）"来表示。假如有如下代码：

def list_check(to_check, the_list):
	for item in the_list:
		if to_check == item:
			return True
	return False
1
2
3
4
5

上面代码功能很简单，就是检查to_check是否在列表the_list中。我们称这个函数的时间复杂度为 $O (n)$ ，其中 $n$ 指列表the_list中的元素个数， $O (n)$ 的意思是算法所需时间的上限随列表中的元素个数线性增长。

在我们描述时间复杂度时，通常会涉及2个数量：

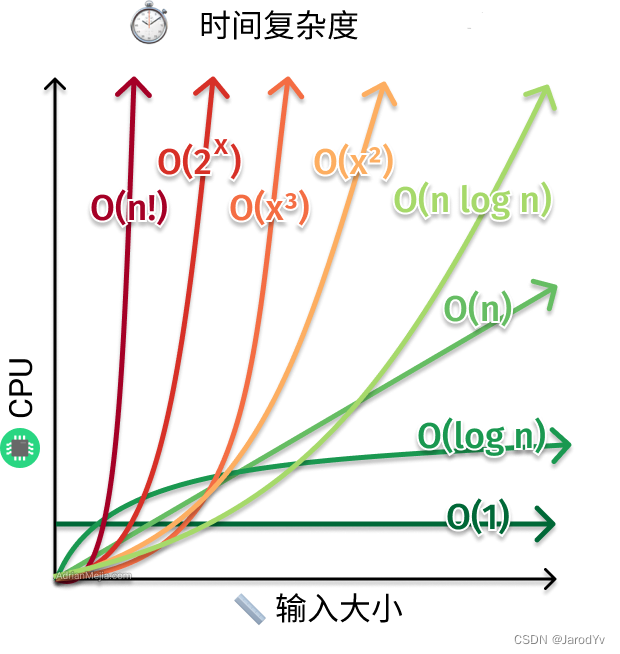
常见复杂度表

Big-O	复杂度	解释
$O (1)$	常量复杂度	无论输入的大小，运行时间始终保持一个常数。例如从哈希表中取值的时间复杂度就是 $O (1)$ 。
$O (n)$	线性复杂度	运行时间随输入大小线性增长。遍历列表就是一个时间复杂度为 $O (n)$ 的操作。
$O(n^{2})$	平方复杂度	运行时间与输入大小呈平方关系。比如冒泡排序、插入排序的时间复杂度为 $O(n^2)$ 。
$O(2^{n})$	指数复杂度	运行时间与输入大小呈指数关系。指数复杂度的算法性能非常低。例如图论中的三色问题就是指数复杂度。
$O(\log_{n})$	对数复杂度	当输入呈指数增长是，运行时间按线性增长。二分法查找就是典型的对数复杂度。

常见复杂度的图像展示

在这里插入图片描述

List是Python中使用最多的数据结构，熟悉List中各操作的时间复杂度对我们优化程序性能有很大帮助

操作	时间复杂度（平均情况）	时间复杂度(最差情况)
`in`	$O (1)$
差集 `s-t`	$O(\text{len}(s))$
交集 `s&t`	$O(\text{min}(\text{len}(s), \text{len}(t)))$	$O(\text{len}(s) \times \text{len}(t))$
并集 `s\\|t`	$O(\text{len}(s) + \text{len}(t))$
对称差集 `s^t`	$O(\text{len}(s))$	$O(\text{len}(s) \times \text{len}(t))$
多重交集 `s1&s2&s3&...&sn`		$(n - 1) * O (l)$ 其中 $\text{max}( \text{len}(s_1),\dots,\text{len}(s_n))$
`s.difference_update(t)`	$O(\text{len}(t) \times \text{len}(s))$
`s.symetric_difference_update(t)`	$O(\text{len}(t))$

deque是python标准库提供的双向队列