【数据结构与算法】图的基本结构介绍 | 邻接表与邻接矩阵编码实战

🚀 作者 ：“大数据小禅”

🚀文章简介：本篇文章对基本数据结构 图进行了一个概述，并使用领接矩阵与邻接表的方式来实现一个图

🚀个人主页： 大数据小禅

图的应用

• 图是一种数据结构，图的应用比较广泛

• 深度优先遍历(DFS)

• 广度优先遍历(BFS)

• 最小生成树 Kruskal Rrim

• 最短路径 Dijkstra Floued Bellman-Ford

• 图是一种数据结构，一个图就是一些节点的集合，这一些节点通过边来连接。是一种多对多的数据结构

• 生活中常见的例子：地铁，每个站与每个站之间都是相连的。

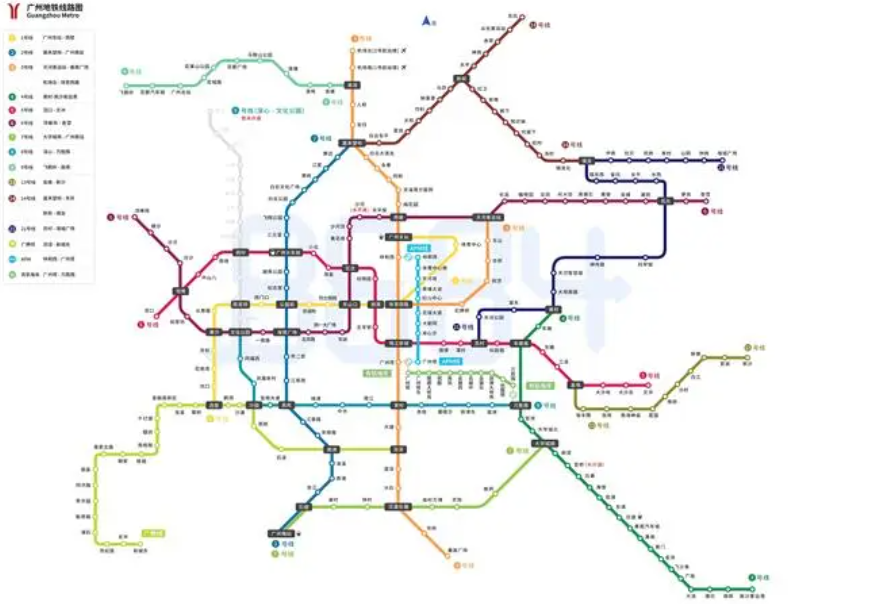
图的分类

• 图主要有以下这几种分类：

• 有向无权图
  

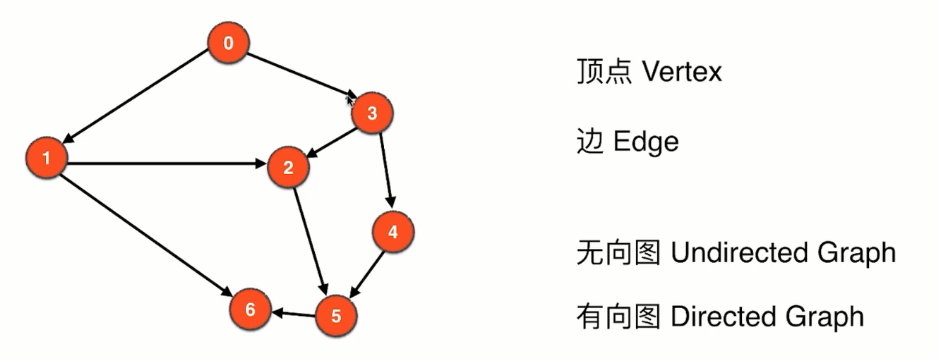
• 无向无权图
  

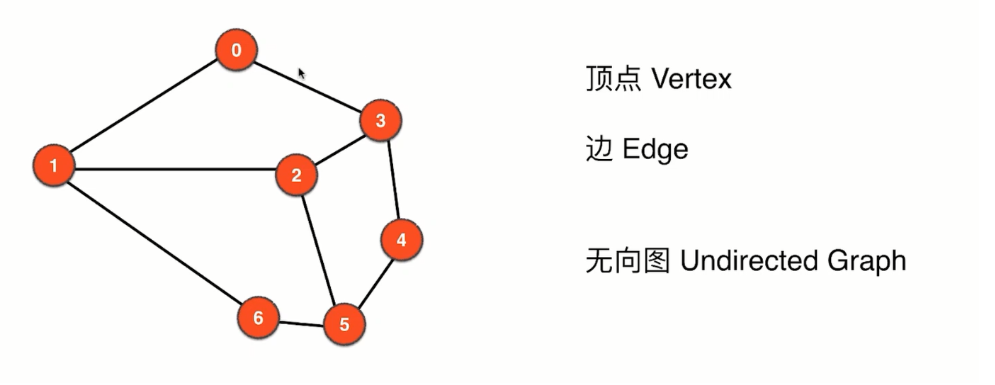
• 无向有全图

• 有向有权图
  

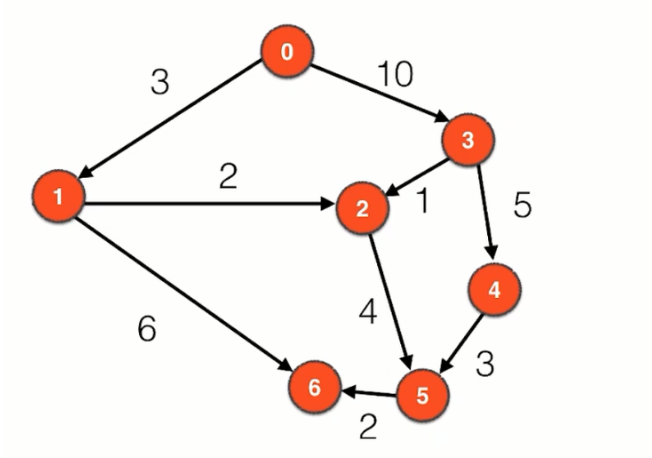
• 图的几个相关术语
  – 顶点 Vertex
  – 边 Edge
  – 有权图
  – 无权图

• 图的表示 邻接矩阵

• 顶点与顶点是相连的，用1来表示，不相连则用0。
  
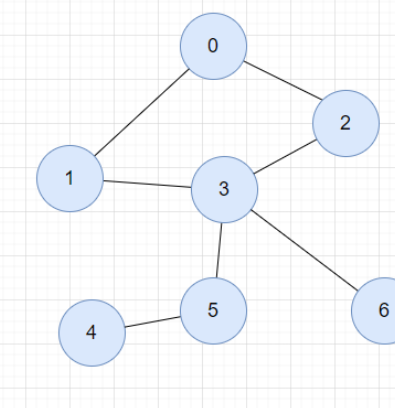
  使用二维数组的方式表示
  

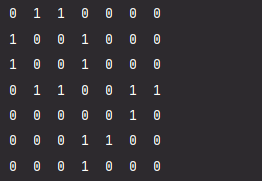
• 编码实现

public class AdjMartix {

    //顶点
    private static int V;
    //边
    private static int E;
    //邻接矩阵
    private static int[][] adj;
    //存放边的信息
    private int[][] edges;
    //从文件中读取图的相关信息
    public AdjMartix()  {

        edges = new int[][]{{7,7},{0,1},{0,2},{1,3},{2,3},{3,5},{3,6},{4,5}};
        V=edges[0][0];  //7
        E=edges[0][1];  //7
        adj=new int[V][E];
        for(int i=1;i<=V;i++){
            int a=edges[i][0];
            int b=edges[i][1];
            adj[a][b]=1;
            adj[b][a]=1;
        }

    }

    //返回 V  E的方法 定义成public 上面定义成private是为了不让用户可以修改
    public int V(){
        return V;
    }
    public int E(){
        return E;
    }

    //图中是否存在某条边
    public boolean hasEdge(int v,int w){
        return adj[v][w]==1;
    }

    //返回顶点v相邻的边  找到顶点v相邻的点就等于找到了相邻的边 返回和V相邻的顶点
    public ArrayList<Integer> adj(int v){
        //验证v是否合法
        validateVertex(v);
        //这里的逻辑可以对比对应的邻接矩阵
        //v是顶点 在矩阵中只要找到v那一行对应的哪一列是1 就代表有连线是相邻的边 adj[v][j]
        ArrayList<Integer> array = new ArrayList<>();
            for(int j=0;j<V;j++){
                if(adj[v][j]==1){
                    array.add(j);
                }
            }
            System.out.println(array);
            return array;
    }

    // 度：顶点有多少个临边  求顶点的度
    public int degree(int v){
        //直接调用上面的方法看对应有几条边度就是多少了
        return adj(v).size();
    }

    //判断参数是否合法
    //invail 无效的
    private void validateVertex(int v){
        if(v<0||v>=V){
            throw new IllegalArgumentException(v+"is invalid");
        }
    }

    private static void showAdj(){
        System.out.printf("V=%d    E=%d \n",V,E);
        for(int i=0;i<V;i++){
            for(int j=0;j<V;j++){
                System.out.printf("%d  ",adj[i][j]);
            }
            System.out.println();
        }
    }


    public static void main(String[] args)  {
        AdjMartix adjMartix = new AdjMartix();
        adjMartix.showAdj();
        adjMartix.adj(3);

    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88

运行结果：

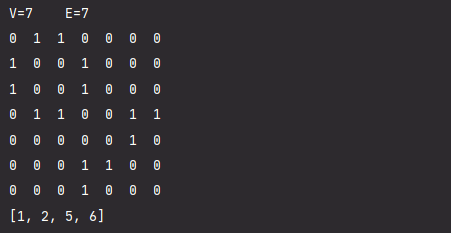
邻接表

• 邻接表它主要就是关心的是存在的边，不存在的边则不管，因此的话不会有空间上的浪费，邻接表=数组+链表。
  

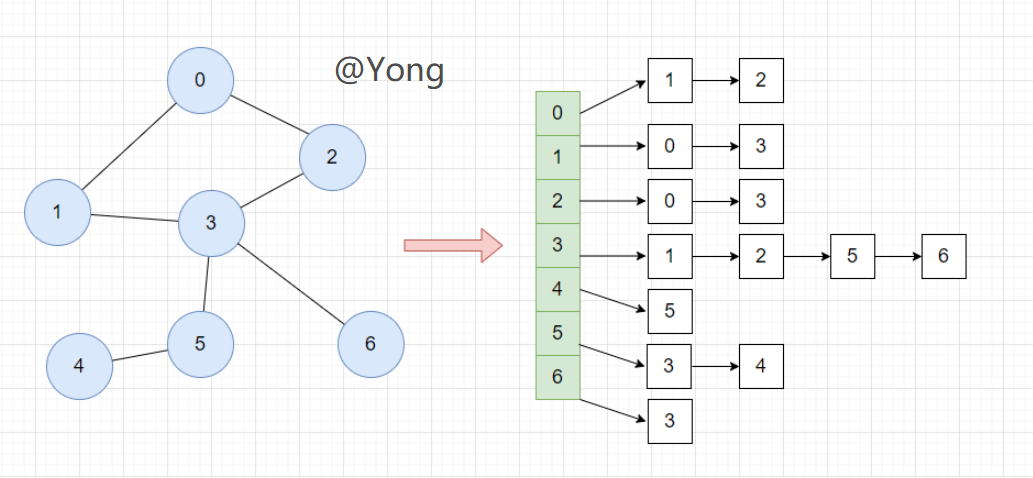
public class GraphXIAOCHAN {
    //顶点
    private static int V;
    //边
    private static int E;
    //邻接表 链表数组   TreeSet低层使用的就是红黑树实现
    private static TreeSet<Integer>[] adj;
    //从文件中读取图的相关信息
    //存放边的信息
    private int[][] edges;
    public GraphXIAOCHAN() {
        edges = new int[][]{{7,7},{0,1},{0,2},{1,3},{2,3},{3,5},{3,6},{4,5}};
        V=edges[0][0];  //7
        E=edges[0][1];  //7
        adj=new TreeSet[V];
        for(int i=0;i<V;i++){
            //遍历数组中的每一个元素 每个元素都开一个空间
            adj[i]=new TreeSet<Integer>();

        }
        for(int i=1;i<=V;i++){
            int a=edges[i][0];
            int b=edges[i][1];
            adj[a].add(b);
            adj[b].add(a);
        }

    }

    //返回 V  E的方法 定义成public 上面定义成private是为了不让用户可以修改
    public int V(){
        return V;
    }
    public int E(){
        return E;
    }

    //图中是否存在某条边
    public boolean hasEdge(int v,int w){
        return adj[v].contains(w);
    }

    //返回顶点v相邻的边  找到顶点v相邻的点就等于找到了相邻的边 返回和V相邻的顶点
    //这里进行修改 返回一个迭代器的方式 向用户隐藏低层的实现
    public Iterable<Integer> adj(int v){
        return adj[v];
    }

    // 度：顶点有多少个临边  求顶点的度
    public int degree(int v){
        //直接调用上面的方法看对应有几条边度就是多少了
        return adj[v].size();
    }

    //判断参数是否合法
    //invail 无效的
    private void validateVertex(int v){
        if(v<0||v>=V){
            throw new IllegalArgumentException(v+"is invalid");
        }
    }

    private static void showAdj(){
        System.out.printf("V=%d    E=%d \n",V,E);
        for(int i=0;i<V;i++){
            System.out.printf("顶点%d： ",i);
            for(int w:adj[i]){
                System.out.printf("%d  ",(w));
            }
            System.out.println();

        }
    }

    public static void main(String[] args) throws FileNotFoundException {
        GraphXIAOCHAN adjset = new GraphXIAOCHAN();
        adjset.showAdj();
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81

运行结果