-
C. Bargain(数学贡献法)

有时,要在讨价还价中达成协议并不容易。现在,萨沙和沃瓦就无法达成协议。萨沙说出了一个尽可能高的价格,然后沃瓦想从这个价格中删除尽可能多的数字。更详细地说,Sasha说出某个整数的价格n,Vova从价格中删除一个非空的(连续的)数字子串,剩下的数字缩小差距,得到的整数就是价格。
例如,Sasha的名字是1213121,Vova可以删除子串1312,结果是121。
允许结果包含前导零。如果Vova去掉了所有的数字,那么价格就被认为是0。
Sasha想提出一些约束条件,使Vova不能直接删除所有数字,但他需要一些支持这些约束条件的论据。首先,他想计算出沃瓦移动后所有可能产生的价格之和。
帮助萨沙计算这个总和。由于答案可能非常大,请将其打印成109+7的模数。
输入
第一行也是唯一一行包含一个整数n(1≤n<10105)。输出
在唯一的一行中,打印所需的109+7模数的和。例子
输入
107
outputCopy
42
输入
100500100500
输出
428101984
注意
考虑一下第一个例子。Vova可以选择删除1、0、7、10、07或107。结果是07、17、10、7、1、0,它们的总和是42。
题解:
这里引入一个概念数学贡献法:一个数的部分对于答案的贡献
对于第i位,我们只考虑它本身对于答案的贡献
举个例子:428101984 中的9
1.删除9前面的位数
我们可以发现无论删去9前面的任何数,9对答案的贡献都是不变的,都是900
那我们就考虑,有多少种删除方式即可
可以转换下概念,对于i-1长度的区间删去,一个区间,肯定要有首尾,相当于任取一位当首,在取一位当尾,就应该是(i - 1)*i种
贡献为(i-1)*i*s[i]*p
p是当前前是什么位(10的多少次方)
2.删除他后面的位数
举个例子。
8 4 3 2 1
对1来说,后面没有,那么贡献是0
对2来说,后面拿1,贡献是2
对3来说,后面拿1和2,贡献是3,后面拿1,贡献是30,后面拿2,贡献是30.
对4来说,后面拿123,贡献是4;后面拿23,21,贡献是40,40;后面拿3,2,1,贡献是400,400,400;
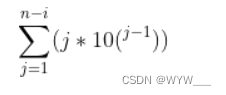
3.删除他本身
都删除本身了,对结果肯定是没有影响的,所以不考虑
(有点像DP对于本身分析)
- #include<iostream>
- #include<algorithm>
- #include<map>
- #include<queue>
- #include<vector>
- #include<cstring>
- using namespace std;
- char s[300050];
- void solve()
- {
- cin >> s+1;
- long long ans = 0;
- int n = strlen(s+1);
- int mod = 1e9+7;
- long long sum = 0;
- long long p = 1;
- for(long long i = n;i >= 1;i--)
- {
- long long now = i*(i-1)/2;//删前面有多少种情况
- ans = (ans+now*(s[i]-'0')%mod*p%mod)%mod;//删i前面对结果贡献
- ans = (ans + sum*(s[i]-'0')%mod)%mod; //删i后面对结果贡献
- sum = (sum + (n-i+1)*p%mod)%mod;//删除后面推导的公式模拟
- p = p*10%mod;//记录位数
- }
- cout<<ans;
- }
- int main()
- {
- int t = 1;
- // cin >> t;
- while(t--)
- {
- solve();
- }
- }
- //
- //abcdef
- //babcdef
- //babcdefedcba
-
相关阅读:
C++ vector模拟实现
sql面试
二叉树路径问题+递归+有关题目
Python自动化测试框架有哪些?
图像分割项目中损失函数的选择
Unity Game FrameWork—模块使用—资源热更新
JS-谈谈你所理解的闭包
2023.09全国青少年软件编程(scratch图形化)等级考试试卷(一级)
VERI-ZEXE: Decentralized Private Computation with Universal Setup
MAC系统和Linux系统下md5获取方法
- 原文地址:https://blog.csdn.net/m0_64158084/article/details/127902581
