（八）Java算法：堆排序（详细图解）

一、前言

1.1、概念

  根据堆的结构可以分为大根堆和小根堆，它是一个完全二叉树，先来了解下什么是大根堆和小根堆吧。

• 大根堆：每个结点的值都大于其左孩子和右孩子结点的值，即：$arr[i]$ > $arr[2\ast i+1]$ && $arr[i]$ > $arr[2\ast i+2]$
• 小根堆：每个结点的值都小于其左孩子和右孩子结点的值，即：$arr[i]$ < $arr[2\ast i+1]$ && $arr[i]$ < $arr[2\ast i+2]$

1.2、大根堆特点

  本文主要以大根堆为例，它的特点如下：

• 数组索引为 $0$ 的位置存放堆顶的元素（大根堆根节点就是最大值了）
• 数组索引为 $i$ 的元素的左右叶子节点的索引分别是$2\ast i+1$ 和 $2\ast i+2$
• 数组索引为 $i$ 的元素的父节点的下标索引为$\frac{i-1}{2}$

二、maven依赖

pom.xml

<dependencies>
    <dependency>
        <groupId>org.springframework.bootgroupId>
        <artifactId>spring-boot-starterartifactId>
        <version>2.6.0version>
    dependency>

    <dependency>
        <groupId>org.projectlombokgroupId>
        <artifactId>lombokartifactId>
        <version>1.16.14version>
    dependency>
dependencies>
1
2
3
4
5
6
7
8
9
10
11
12
13

三、流程解析

3.1、初始建堆

  先把我们数组的元素转化为大根堆。

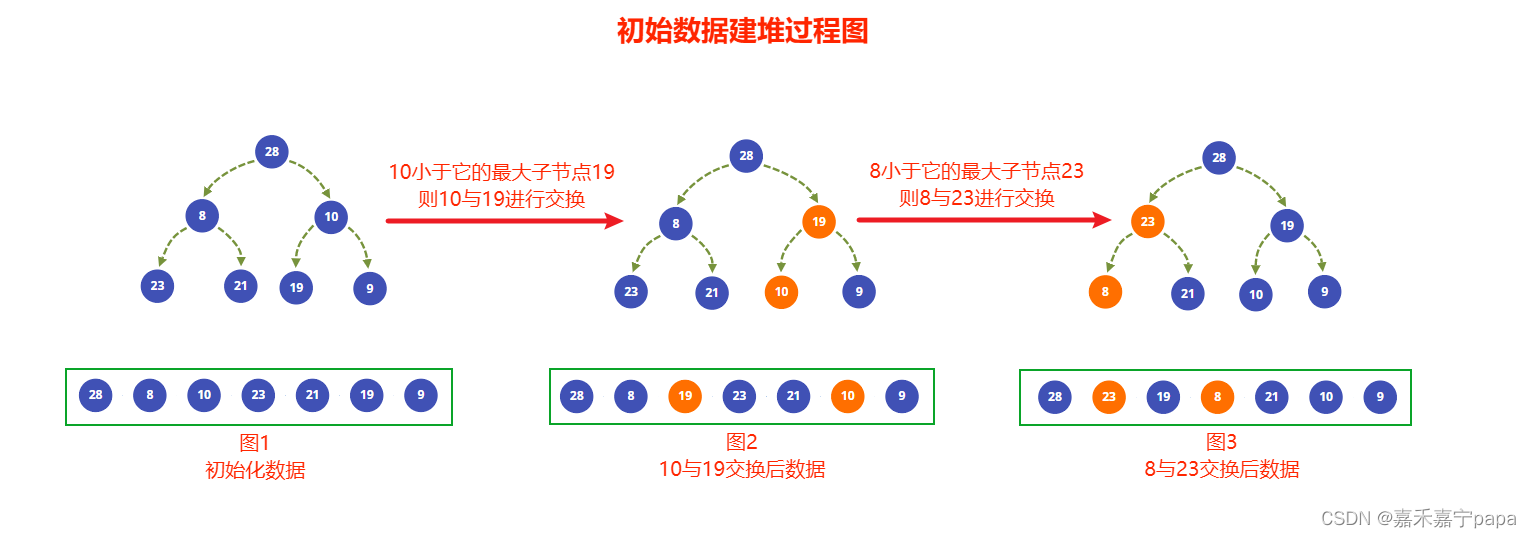
• 数组索引为 $i$ 的元素的左右叶子节点的索引分别是$2\ast i+1$ 和 $2\ast i+2$，我们可以把数组转化为图1的树，这个是初始化的数据
• 图1中最后一个父节点是$10$，它不满足大根堆的条件，因为它的子节点的值$19$比它大，所以我们交换他们的值得到图2，当前的节点就满足大根堆了，然后继续下一个节点
• 往前继续找到父节点$8$（也就是从最右的父节点一直往前遍历），它不满足大根堆的条件，因为它的子节点的值$23$比它大，所以交换 $8$ 和 $23$ 得到图3，然后继续下一个节点
• 下一父节点是$28$，它的值比两个子节点的值都大，已经满足大根堆的条件了，建堆完成

3.2、堆化第一步

  我们这一步是接着上面建堆的结果的，也就是以图3为基础变化的。

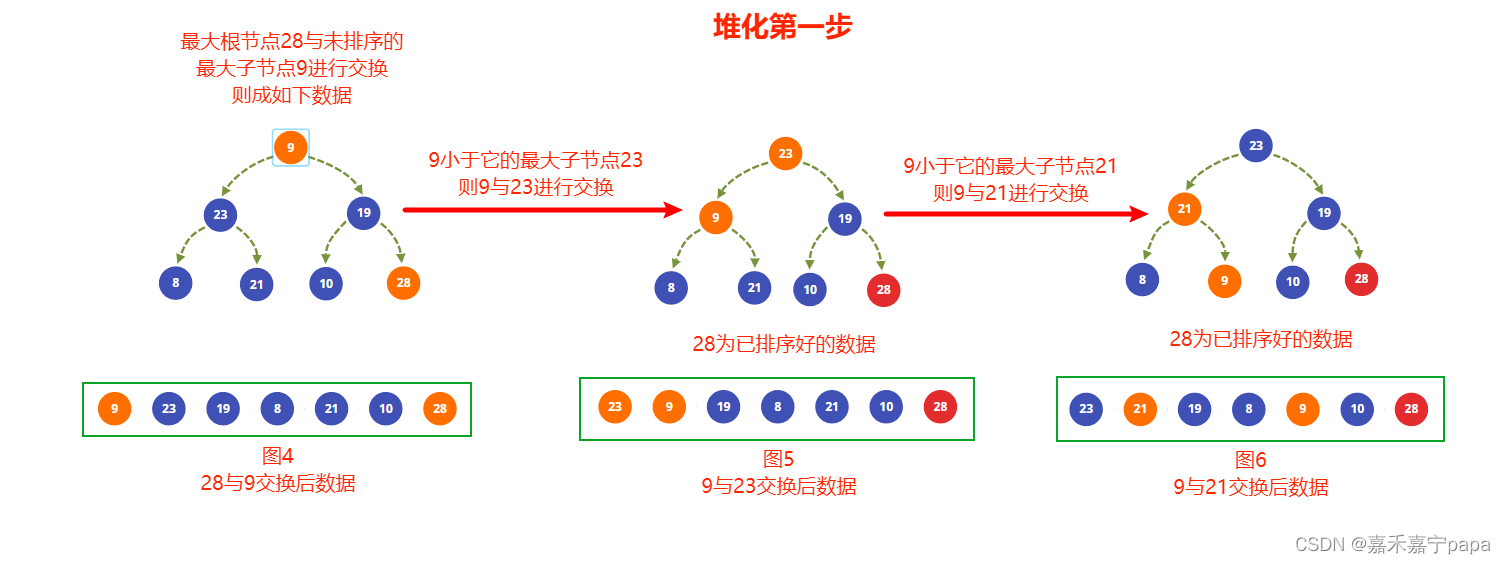
• 通过上一步建堆时我们已经得到了大根堆了，也就是图3，我们把大根堆的值和最右未排序的子节点进行交换，也就是 $28$ 和 $9$ 得到图4，则 $28$ 就是排序完成的数据
• 从图4中知道，排除排序好的节点（$28$）来看，$19$ 和 $23$ 满足大根堆，不用变化，但是根节点9不满足，因为它比它最大子节点$23$小，所以交换 $9$ 和 $23$ 得到图5
• 交换后的节点$9$还是不满足大根堆条件，因为它比最大子节点 $21$小，所以交换 $9$ 和 $21$ 得到图6，$9$ 已经没有子节点了，建堆完成

3.2、堆化第二步

  我们这一步是接着上面建堆的结果的，也就是以图6为基础变化的。

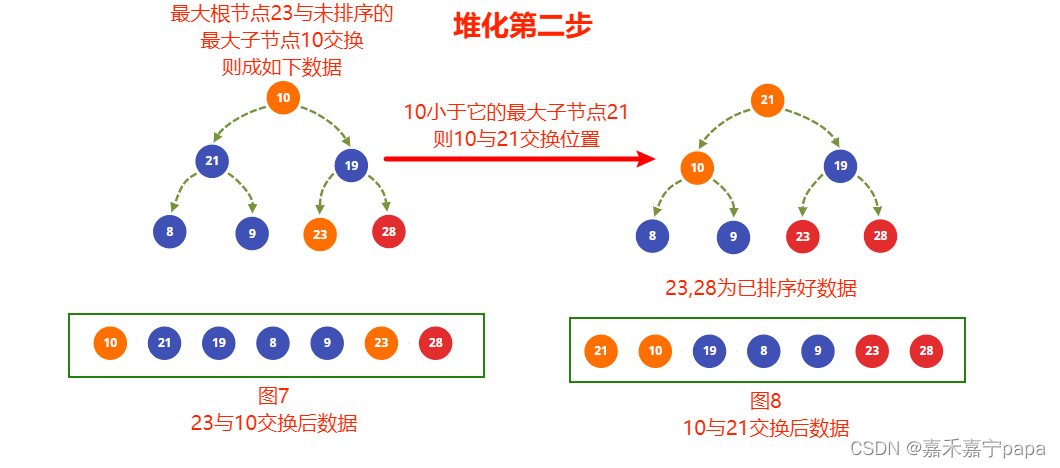
• 上一步建堆时我们已经得到了大根堆了，我们把大根堆的值和最右未排序的子节点进行交换，也就是 $23$ 和 $10$ 得到图7，则 $23$ 就是排序完成的数据
• 从图7中知道，排除排序好的节点（$23$、$28$）来看，$19$ 和 $21$ 满足大根堆，不用变化，但是根节点$10$不满足，因为它比它最大子节点$21$小，所以交换 $10$ 和 $21$ 得到图8
• 图8中，交换后的节点$10$已经满足大根堆的条件了，建堆完成

3.3、堆化第三步

  我们这一步是接着上面建堆的结果的，也就是以图8为基础变化的。

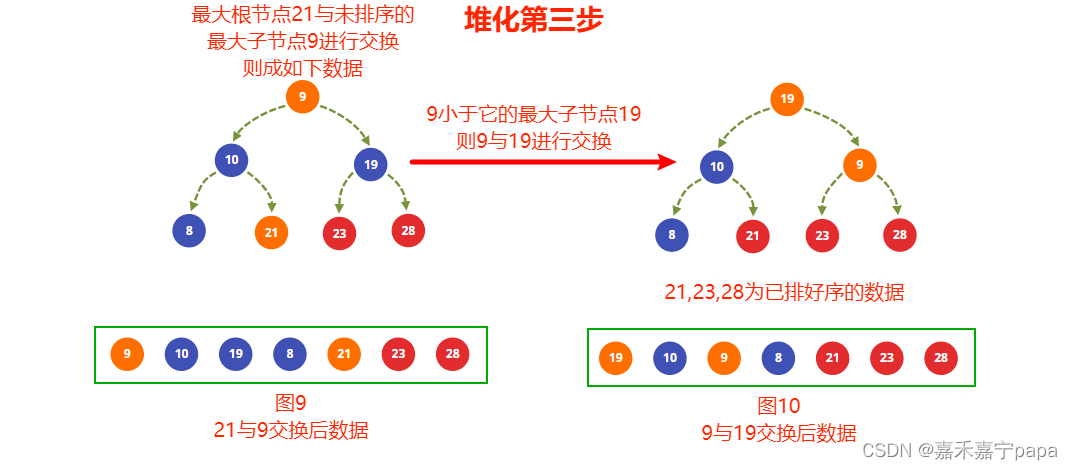
• 上一步建堆时我们已经得到了大根堆了，我们把大根堆的值和最右未排序的子节点进行交换，也就是$21$和$9$得到图9，则 $21$ 就是排序完成的数据
• 从图9中知道，排除排序好的的节点（$21$、$23$、$28$）来看，$19$ 和 $10$ 满足大根堆，不用变化，但是根节点$9$不满足，因为它比它最大子节点$19$小，所以交换 $9$ 和 $19$ 得到图10
• 图10中，交换后的节点$9$（除去排序完成的没有子节点了）已经满足大根堆的条件了，建堆完成

3.4、堆化第四步

  我们这一步是接着上面建堆的结果的，也就是以图10为基础变化的。

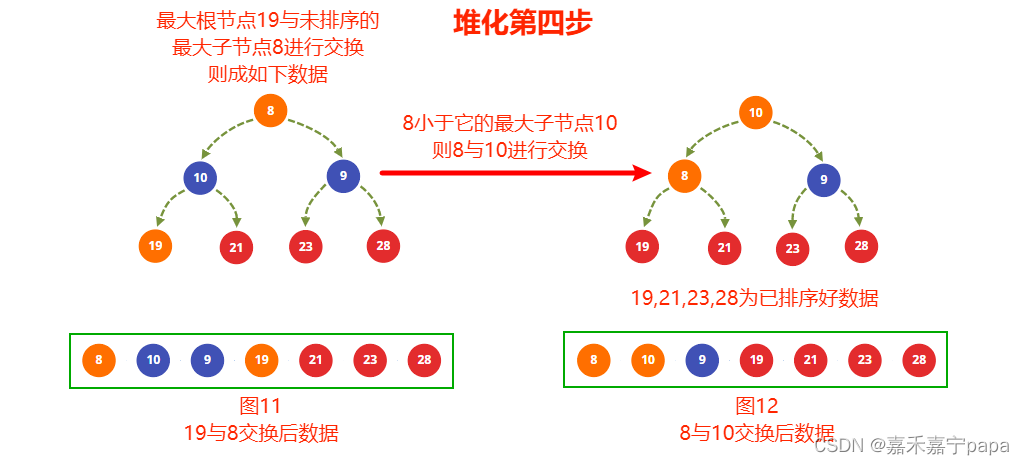
• 上一步建堆时我们已经得到了大根堆了，我们把大根堆的值和最右未排序的子节点进行交换，也就是$19$和$8$得到图11，则 $19$ 就是排序完成的数据
• 从图11中知道，排除排序好的的节点（$19$、$21$、$23$、$28$）来看，$9$ 和 $10$ 满足大根堆，不用变化，但是根节点$8$不满足，因为它比它最大子节点$10$小，所以交换 $8$ 和 $10$ 得到图12
• 图12中，交换后的节点$8$（除去排序完成的没有子节点了）已经满足大根堆的条件了，建堆完成

3.5、堆化第五步

  我们这一步是接着上面建堆的结果的，也就是以图12为基础变化的。

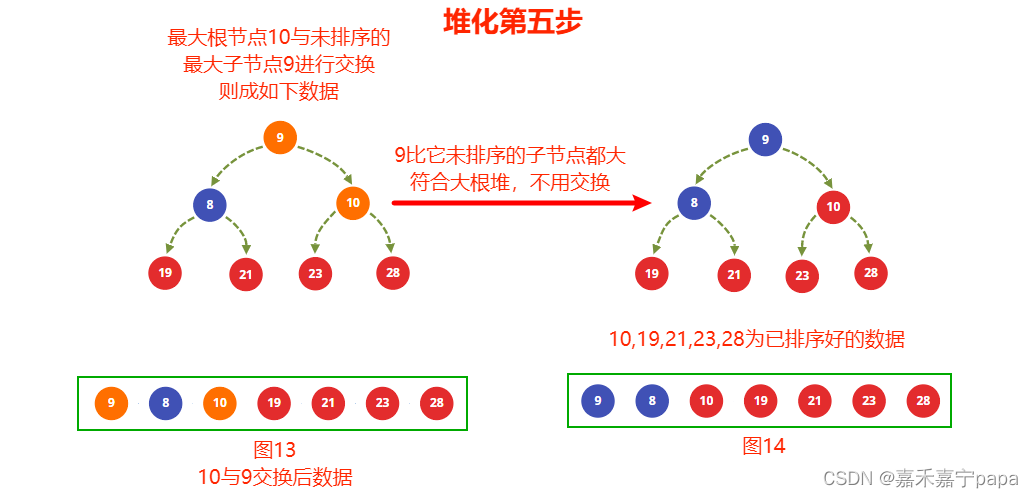
• 上一步建堆时我们已经得到了大根堆了，我们把大根堆的值和最右未排序的子节点进行交换，也就是 $10$ 和 $9$ 得到图13，则 $10$ 就是排序完成的数据
• 从图13中知道，排除排序好的的节点（$10$、$19$、$21$、$23$、$28$）来看，交换后的节点$8$（除去排序完成的没有子节点了）已经满足大根堆的条件了
• 最后结果就是图14，节点都已经满足大根堆的条件了，建堆完成

3.6、堆化第六步

  我们这一步是接着上面建堆的结果的，也就是以图14为基础变化的。

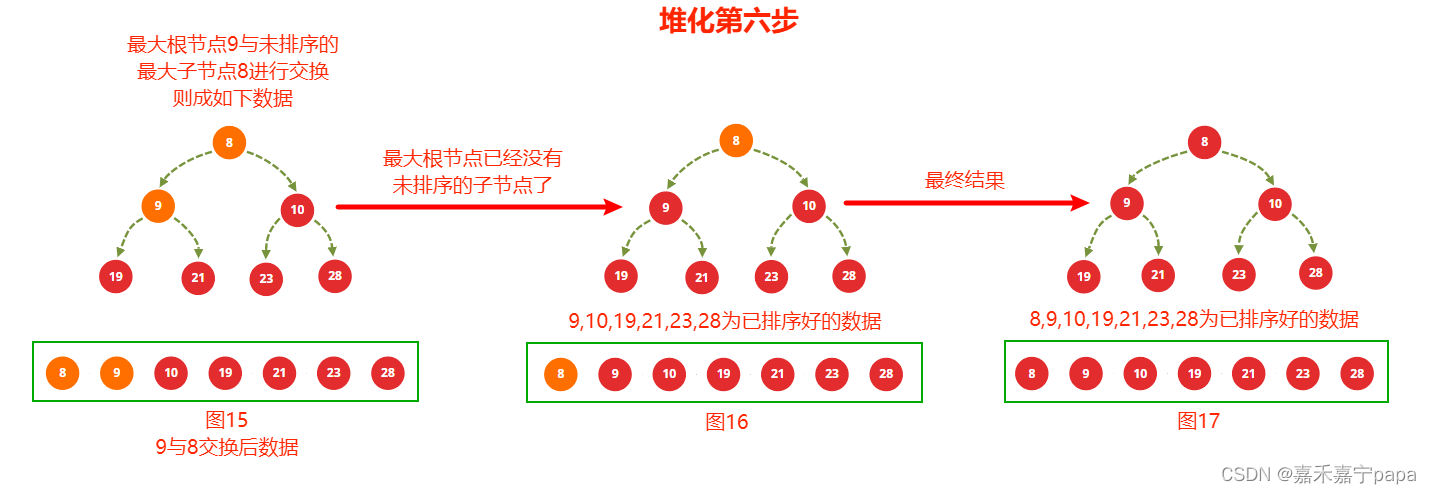
• 上一步建堆时我们已经得到了大根堆了，我们把大根堆的值和最右未排序的子节点进行交换，也就是 $9$ 和 $8$ 得到图15，则 $9$ 就是排序完成的数据
• 从图15中知道，排除排序好的的节点（$9$、$10$、$19$、$21$、$23$、$28$）来看，只有一个根节点节点$8$了，也就是图16，不用比较了，最后的结果就是全部排序完的图17，到此我们的排序就完成了

四、编码实现

4.1、代码实现

public static void heapSort(int[] arr) {
    // 获取数组长度
    int length = arr.length;
    // 数组索引为 i 的元素的父节点的下标索引为：i-1/2 得到
    // 因为下标从0开始，最后一个子节点（length-1）减去1再除以2得到父节点（length-1-1）/2=length / 2 - 1
    // 我们从最后一个父节点开始遍历直到根节点（父节点会和子节点进行比较的）
    for (int i = length / 2 - 1; i >= 0; i--) {
        // 把数组转化为堆，我们称之为建堆
        buildHeap(arr, i, length);
    }
    log.info("数组建堆后的结果：{}", arr);
    // 排序，因为之前已经完成了建堆，意味着，根节点就是我们需要的值
    for (int i = length - 1; i >= 0; i--) {
        // 将当前根节点与未排序的最大子节点进行交换
        swap(arr, 0, i);
        // 剩下的元素继续建堆,要理解i--,刚刚交换的根节点的值就是已排序的不会参与遍历了
        buildHeap(arr, 0, i);
    }
}

private static void buildHeap(int[] arr, int i, int length) {
    // 大顶堆的节点调整
    while (true) {
        // 定义最大节点的位置
        int maxPos = i;
        // 检查在未排序列表中，当前节点的值是不是小于它的左子节点(2i+1)
        if (i * 2 + 1 < length && arr[i] < arr[i * 2 + 1]) {
            maxPos = i * 2 + 1;
        }
        // 检查在未排序列表中，同时当前的最大节点和i节点的右子节点（2i+2）也比较找出最大值的节点
        // 也就是找出父节点，左节点，右节点三者中的最大节点值
        if (i * 2 + 2 < length && arr[maxPos] < arr[i * 2 + 2]) {
            maxPos = i * 2 + 2;
        }
        // maxPos没变说明已经找不到比当前节点大的了
        if (maxPos == i) {
            break;
        }
        // 交换两个节点（当前节点和最大值的节点进行交换）
        // 这里就是父节点和子节点中那个较大的节点进行交换
        swap(arr, i, maxPos);
        // 继续往下处理这个过程（）也就是继续处理最大节点，看它是否满足大根堆的条件（比它的子节点都大）
        i = maxPos;
    }
    log.info("大顶堆的节点调整后结果：{}", arr);
}

private static void swap(int[] arr, int i, int j) {
    log.info("交换数据：{}和{}交换", arr[i], arr[j]);
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

public static void main(String[] args) {
    int[] arr = new int[]{28, 8, 10, 23, 21, 19, 9};
    log.info("要排序的初始化数据：{}", arr);
    //从小到大排序
    heapSort(arr);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

  一定要结合本地第一节的概念和特点去看代码，才会事半功倍。

4.2、运行结果：

要排序的初始化数据：[28, 8, 10, 23, 21, 19, 9]
交换数据：10和19交换
大顶堆的节点调整后结果：[28, 8, 19, 23, 21, 10, 9]
交换数据：8和23交换
大顶堆的节点调整后结果：[28, 23, 19, 8, 21, 10, 9]
大顶堆的节点调整后结果：[28, 23, 19, 8, 21, 10, 9]
数组建堆后的结果：[28, 23, 19, 8, 21, 10, 9]
交换数据：28和9交换
交换数据：9和23交换
交换数据：9和21交换
大顶堆的节点调整后结果：[23, 21, 19, 8, 9, 10, 28]
交换数据：23和10交换
交换数据：10和21交换
大顶堆的节点调整后结果：[21, 10, 19, 8, 9, 23, 28]
交换数据：21和9交换
交换数据：9和19交换
大顶堆的节点调整后结果：[19, 10, 9, 8, 21, 23, 28]
交换数据：19和8交换
交换数据：8和10交换
大顶堆的节点调整后结果：[10, 8, 9, 19, 21, 23, 28]
交换数据：10和9交换
大顶堆的节点调整后结果：[9, 8, 10, 19, 21, 23, 28]
交换数据：9和8交换
大顶堆的节点调整后结果：[8, 9, 10, 19, 21, 23, 28]
交换数据：8和8交换
大顶堆的节点调整后结果：[8, 9, 10, 19, 21, 23, 28]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

扩展

  实际在我们的数据结构中，有一种队列采用的也是堆排序，那就是PriorityQueue（优先队列），大家可以作一个了解。

package com.alian.algorithm.sort;

import lombok.extern.slf4j.Slf4j;

import java.util.Iterator;
import java.util.PriorityQueue;

@Slf4j
public class HeapSort {

    public static void heapSort(int[] arr) {
        PriorityQueue<Integer> queue = new PriorityQueue<>();
        for (int value : arr) {
            queue.offer(value);
        }
        Iterator<Integer> iterator = queue.iterator();
        while (iterator.hasNext()) {
            log.info("排序后的数据：{}", queue.poll());
        }
    }

    public static void main(String[] args) {
        int[] arr = new int[]{28, 8, 10, 23, 21, 19, 9};
        log.info("要排序的初始化数据：{}", arr);
        //从小到大排序
        heapSort(arr);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

运行结果：

要排序的初始化数据：[28, 8, 10, 23, 21, 19, 9]
排序后的数据：8
排序后的数据：9
排序后的数据：10
排序后的数据：19
排序后的数据：21
排序后的数据：23
排序后的数据：28
1
2
3
4
5
6
7
8