基于径向基函数RBF神经网络的非线性函数拟合研究-含Matlab代码

一、RBF神经网络基本原理

1988年Broomhead和Lowe将径向基函数(radial basis function, RBF)引入神经网络，形成了RBF神经网络。RBF神经网络是一种三层的前馈网络， 其基本思想是:利用RBF作为隐单元的“基”构成隐含层空间，把低维的输入矢量通过投影变换到高维空间，使原本线性不可分的问题变得线性可分。图1为RBF神经网络基本结构示意图。

图1 RBF神经网络基本结构

由RBF构成的隐含层空间，可以将输入矢量直接映射到隐空间， 从而不需要通过权联接， 因此输入层和隐含层之间的联接权值均为1。隐含层实现对输入向量的非线性投影， 而输出层则负责最后的线性加权求和。RBF神经网络中待学习优化的参数包括：径向基函数的中心、方差以及隐含层到输出层的联接权值。输出层负责通过线性优化策略来实现对权值的优化，学习速度通常较快；而隐含层则需要采用非线性优化的方法对激活函数的参数进行调整， 故而其学习速度相对较慢。RBF神经网络的参数学习方法按照径向基函数中心的选取有不同的类型， 主要包括自组织选取法、随机中心法、有监督中心法和正交最小二乘法。RBF神经网络学习过程主要由两个阶段构成， 第一阶段为无监督学习过程， 实现隐含层基函数的中心及方差的求解; 第二阶段是有监督学习过程， 确定隐含层到输出层之间的联接权值。RBF神经网络属于局部逼近网络， 省略了隐含层权值的学习行为， 避免了误差在网络中耗时的逐层传递过程， 因此该网络的学习收敛速度非常快。和其他神经网络相比， RBF神经网络可以以任意精度逼近任意的非线性函数，具有最佳逼近性能、分类能力和全局最优特性， 而且拓扑结构简单，计算量小， 网络的适用性好， 可以动态确定网络结构和隐层单元的数据中心和扩展常数， 收敛速度快。

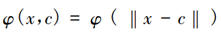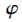径向基函数是一个取值仅依赖于距定点c距离的实值函数， 任意一个满足 特征的函数 均为径向基函数， 简化情况下也可以是到原点的距离， 即 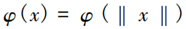。采用高斯核函数作为径向基神经网络的基函数， 则径向基神经网络隐单元的输出为: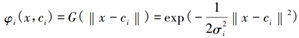

其中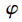， 为径向基函数，x为样本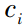， 为核函数第i个中心点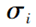， 为函数第i个中心点的宽度。核函数中心点的选取十分关键，不恰当的中心位置无法使网络正确反映输入样本空间的实际分布情况，对输入空间不能很好地进行拟合。核函数中心点的宽度控制了函数的径向作用范围，是影响 RBF神经网络性能的重要因素。当宽度太小时， 类间的分界线就会变得比较模糊，就会降低分类精度; 当宽度太大时， 基函数的覆盖区域就会变得相对较小， 从而降低网络的泛化能力。

则 RBF神经网络的输出为:

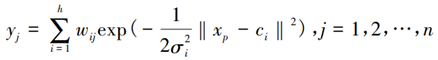
其中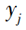， 表示RBF神经网络的输出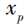， 表示第 p 个输入样本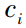， 表示第 i 个中心点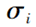， 表示函数第 i 个中心点的宽度， 表示隐含层神经元 i 与输出层神经元 j之间的联接权值系数， h 表示隐含层的节点数， n 是输出的样本数或分类数。

二、模型建立

预先设定一个非线性函数，如下式所示，假定函数解析式不清楚的情况下，随机产生x1，x2和由这两个变量按下式得出的y。将x1，x2作为RBF网络的输入数据，将y作为RBF网络的输出数据，分别建立近似和精确RBF网络进行回归分析，并评价网络拟合效果。

三、RBF网络拟合结果分析

由图2可知，神经网络的训练结果能较好逼近该非线性函数F，由误差图上看，神经网络的预测效果在数据边缘处的误差较大；在其他数值处的拟合效果很好。网络的输出和函数值之间的差值在隐藏层神经元的个数为50时已经接近于0，说明网络输出能非常好地逼近函数。

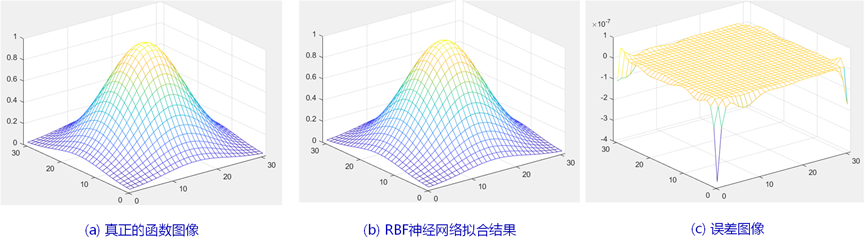
图2 RBF神经网络拟合结果

图3 网络训练结果

四、注意事项

尽管RBF网络的输出是隐单元输出的线性加权和，并且网络学习速率快，但并不等于RBF神经网络就可以取代其他前馈网络。这是因为RBF网络很可能需要比BP神经网络多得多的隐含层神经元来达到预期的训练目标。BP网络采用 sigmoid()函数，这样的神经元有很大的输出可见区域，而径向基网络使用的径向基函数输入空间区域就很小，这就不可避免地导致了再输入空间较大时，需要更多的径向基神经元。

五、参考文献

[1] 穆云峰.RBF神经网络学习算法在模式分类中的应用研究[D].大连:大连理工大学,2006.

六、Matlab代码获取

上述Matlab代码，可私信博主获取。

https://download.csdn.net/download/m0_70745318/87773734

---

博主简介：研究方向涉及智能图像处理、深度学习等领域，先后发表过多篇SCI论文，在科研方面经验丰富。任何与算法、程序、科研方面的问题，均可私信交流讨论。

---