C++笔试题之n阶楼梯问题：每次只能走1阶或2阶，有多少种方法走完

n阶楼梯问题：每次只能走1阶或2阶，有多少种方法走完

1.方法一：采用递归的方式

走到第n阶时可能是从第n-1阶走一步到的，也可能是从n-2阶走两阶到的，设F(n)为走到n阶的种数，则F(n)=F(n-1)+F(n-2)。当n=1时，F(1)=1，n=2时，F(2)=2，这是一个动态规划问题。其实就是一个斐波那契数列。
 

#include <iostream>
 
long long func(int n)
{
    if(1 == n || 2 == n)
    {
        return n;
    }
    else if(n > 2)
    {
        return func(n - 1) + func(n - 2);
    }
    else
    {
        return -1;  // n 非法
    }
}
 
int main()
{
    std::cout << func(50) << std::endl; // 输出20365011074
    
    system("pause");
    
    return 0;
}

2.方法二：采用非递归的方式

int main()
{
    long long a[90];
    int n = 50;
    a[1] = 1;
    a[2] = 2;
    for(int i = 3; i <= n; i++)
    {
        a[i] = a[i-1]+a[i-2];
    }
 
    std::cout << a[n] <<std::endl; // 输出20365011074
 
    system("pause");
 
    return 0;
}

3.递归的效率问题

对比两种方式可以发现，如果楼梯是50阶，第一种方法在我的core i7 6核电脑上要将近1分钟才能输出结果，而第二种方法几乎瞬间输出。

下面是通过递归实现“斐波那契”的原理图：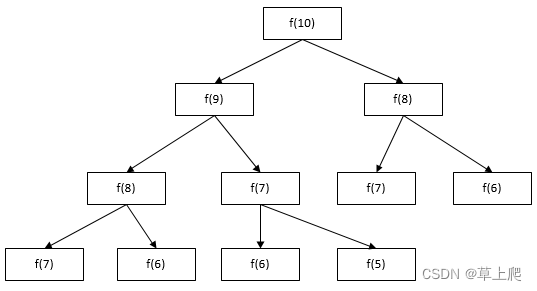

由图可见，仅仅是对f(10)进行计算的原理图，而且仅仅画出了4层，就出现了相同结果的大量重复，如果计算f(50)，这种单纯的递归实现就会出现严重的性能问题。即随着n值的递增，为求出最终的f(n)，重复的项会急剧增加。用递归计算这种方法的时间复杂度是以n的指数方式递增，时间复杂度为O(2^n)。

递归的方式之所以有大量重复，在于它是从上向下计算的。而非递归方式是从下向上的计算的，这样可以保证相同的数不需要重复去计算，因为中间出现过的变量值，已经计算出来而且进行保存，可以快速地拿来使用。即由f(0)和f(1)算出f(2)，由f(1)和f(2)算出f(3)……，最终这样下来，计算的时间复杂度为O(n)。

参考链接：【算法】斐波那契数列的效率问题_暂7师师长常乃超的博客-CSDN博客