【Leetcode】1259. Handshakes That Don‘t Cross

题目地址：

https://leetcode.com/problems/handshakes-that-dont-cross/description/

有$n$个点（$n$为正偶数），可以想象为其在某个正$n$边形的顶点上。要将这些点两两配对，配对的点连一条线段。要求线段之间互不相交，下面是$6$个点的例子：

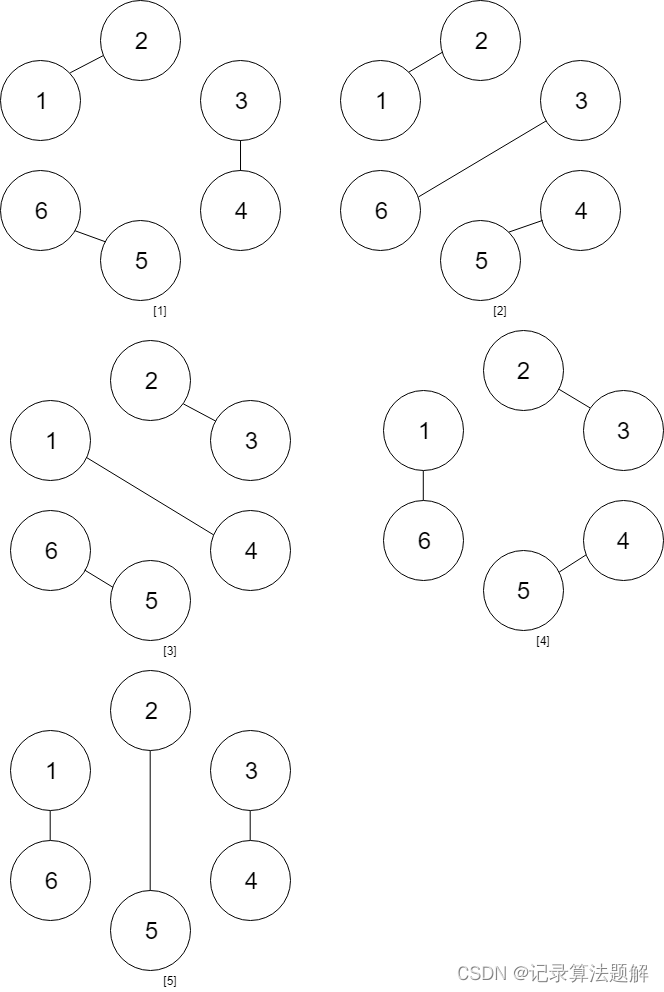
问有多少个连线方案数。答案模$10^9+7$返回。

设$f[n]$是$n$个点的方案数，则$f[0]=1$（没有点，不连也是一种方案）。$f[n]$可以按$1$号点和谁连来分类，如果$1$与$k$相连，那么将剩余$n-2$个点分成两部分，一部分$k-2$个点，另一个$n-k$个点，并且$k$是偶数，那么这种分法方案数为$f[k-2]f[n-k]$。所以$f[n]={\sum }_{k=0}^{n/2-1}f[2k]f[n-2-2k]$。令$g[k]=f[2k]$，则$g[k]={\sum }_{i=0}^{k}g[i]g[k-1-i]$。返回$g[n/2]$即可。这种序列其实就是Catalan数。代码如下：

class Solution {
 public:
  int numberOfWays(int n) {
    int MOD = 1e9 + 7;
    n >>= 1;
    long f[n + 1];
    memset(f, 0, sizeof f);
    f[0] = 1;
    for (int k = 1; k <= n; k++)
      for (int x = 0; x < k; x++) f[k] = (f[k] + f[x] * f[k - 1 - x]) % MOD;

    return f[n];
  }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

时间复杂度$O(n^2)$，空间$O(n)$。