基于费舍尔判别分析的故障与诊断（lunwen+文献综述+翻译及原文+MATLAB程序）

目 录
1 引 言 1
1.1 故障诊断技术的研究背景 1
1.1.1 故障诊断技术概述 1
1.1.2 故障诊断技术的研究对象 1
1.1.3 故障诊断技术研究的必要性 2
1.2 国内外基于费舍尔的故障诊断技术研究进展 3
1.2.1 基于费舍尔的故障诊断技术的研究历史 3
1.2.2 基于费舍尔的故障诊断技术发展趋势 4
1.3 本次设计主要工作内容 7
2 故障诊断方法研究 9
2.1 基于解析模型的方法 9
2.1.1 状态观测法 9
2.1.2 参数估计法 9
2.1.3 等价关系法 10
2.2 基于知识的方法 10
2.2.1 专家系统 10
2.2.2 人工神经网络 10
2.2.3 因果分析法 11
2.2.4 模糊理论 11
2.3 基于数据分析的方法 11
2.3.1 费舍尔法 11
2.3.2 偏最小二乘法 12
2.3.3 Fisher判别分析法 12
2.3.4 规范变量分析法 12
2.4.5 子空间法 13
2.4.6小波变换法 13
3 基于费舍尔的故障诊断技术研究 14
3.1 费舍尔的研究背景 14
3.2 费舍尔的数学思想 14
3.3 费舍尔的实现方法 15
3.3.1 费舍尔的分解方法 15
3.3.2 主元得分向量的计算方法 16
3.3.3 确定主元个数的方法 17
3.3.4 主元模型的建立 18
3.3.5 费舍尔的统计量 19
3.4 基于费舍尔的故障诊断流程 20
4 基于费舍尔的故障诊断技术应用仿真研究 22
4.1 应用仿真环境 22
4.1.1 田纳西–伊斯曼过程 22
4.1.2 田纳西–伊斯曼过程工艺流程 22
4.2 仿真研究 23
4.2.1 基于费舍尔的故障诊断步骤 23
4.2.1 仿真概述 24
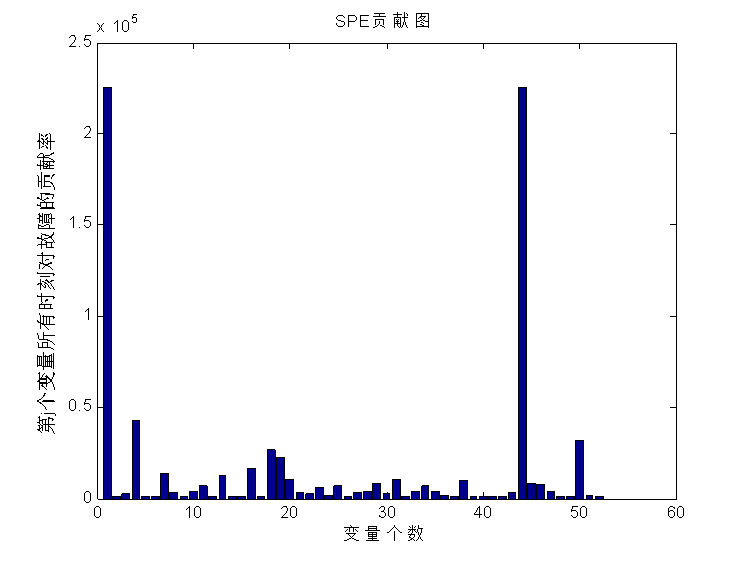
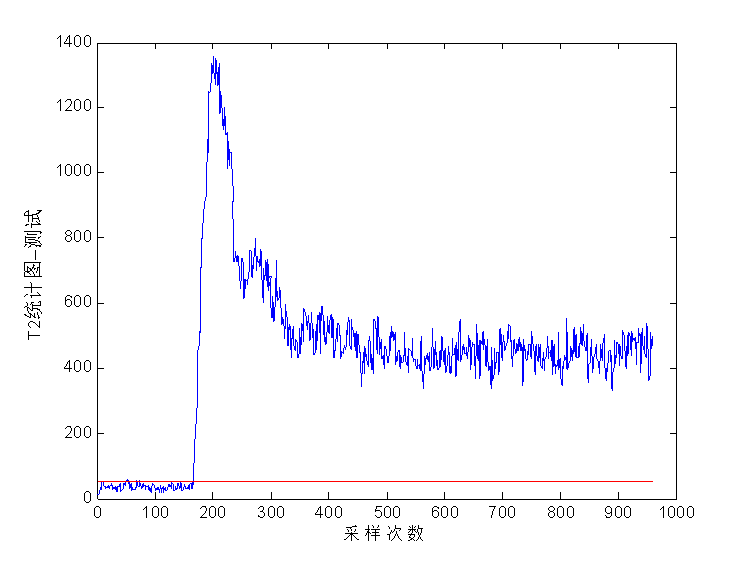
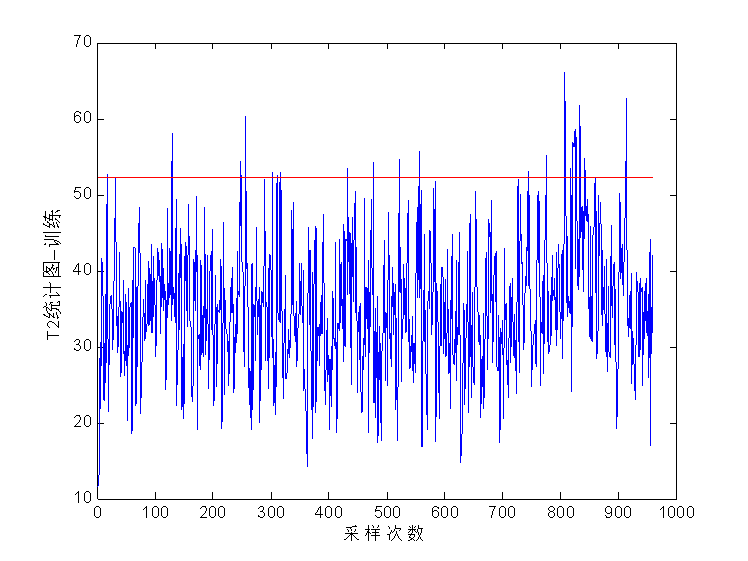
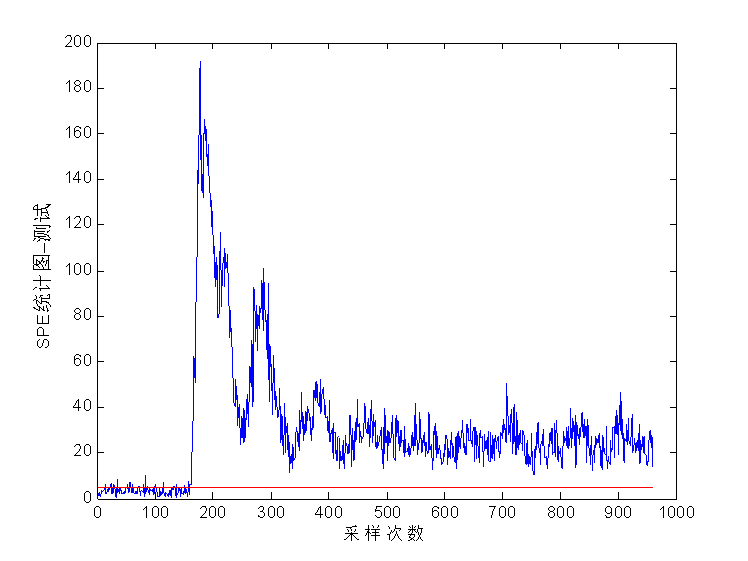
4.2.3 仿真结果 25
结 论 29
致 谢 30
参考文献 31
附录A：英文原文 33
附录B：汉语翻译 40
1.3 本次设计主要工作内容
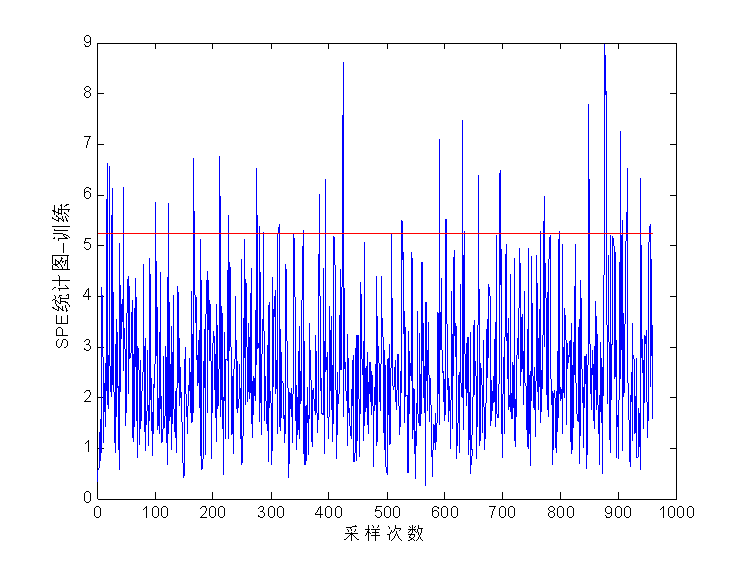
本文通过查阅相关资料文献，通过对多种故障诊断方法的研究，选取基于费舍尔（FDA）的方法作为本文设计故障诊断系统的基础。本文主要研究了基于费舍尔的数学原理和实现过程，并使用田纳西–伊斯曼过程TEP (Tennessee Eastman Process)平台产生仿真数据，利用MATLAB软件建立故障检测与诊断模型。通过和(或SPE)统计量与其阈值的判断，并通过贡献率图对系统进行故障诊断。实验表明，基于FDA的故障诊断方法能够对过程的非正常变化做出反应，也能较正确地找出发生故障的原因以及相应环节。

2 故障诊断方法研究
系统故障是指系统中的重要变量或特性出现了较大偏差，在一定时间内系统主要功能指标超出规定的范围。从广义上来看，故障可以理解为系统的任何异常现象，使系统表现出所不期望的特性。故障诊断技术是一门综合性的技术，涉及到多门学科，如现代控制理论、可靠性设计、数理统计、模糊集理论、信号处理、模式识别、人工智能等。
故障诊断技术所使用的方法目前尚未有一个统一的分类标准，常见的分类方式将其分为三类：基于解析模型的方法、基于知识的方法、基于数据分析的方法[12]。
2.1 基于解析模型的方法
基于解析模型的方法又称为解析冗余法。该方法以系统的数学模型为基础，利用状态观测器、卡尔曼滤波器、参数估计辩识、等价空间方程等方法产生残差，然后基于某种准则或阈值对残差进行分析与评价，实现故障诊断。由于该方法能与系统的机理模型紧密结合，可以方便地实现监控、容错控制、故障重构等。根据残差的产生方式可细分为状态观测法、参数估计法和等价关系法等。
2.1.1 状态观测法
当故障与执行器、传感器或状态变量的变化密切相关时，状态观测法是一种比较合适的故障检测与诊断方法。使用状态观测法或卡尔曼滤波器重构被控过程的状态，与可测变量相比较构成残差序列，通过统计检验对残差进行分析，当残差超过了设定的阈值，就可以确认检测到故障的发生。根据状态对应的物理意义，可进一步对故障进行辨识及决策。用状态观测法进行故障检测与诊断需要一个合适准确的系统机理模型，该模型的建立对故障的辨识过程极为有利。但是对于某些大型的工业工程来说，建立一个准确的系统模型并非轻而易举的事情。
2.1.2 参数估计法
如果过程故障是和模型参数的变化密切联系的，并且恰当准确的数学模型容易得到，则用参数估计法进行故障诊断比较合适。使用该方法时，首先建立被控过程的输入输出参数模型，然后根据系统的输入输出序列计算出模型参数，由模型参数估计过程物理参数，将它与过程中的实际物理参数相比较得到残差序列。最后根据残差序列的变化检测故障是否发牛，当确定有故障发生时，再根据参数的变化进行故障分离、估计及决策。一种强跟踪滤波器理论可用于非线性系统的在线故障诊断。用参数估计法进行故障诊断需要对系统的机理有深入的了解，这样才能在检测到故障的同时，迅速地对故障原因进行分析。
2.1.3 等价关系法
该方法是要检查系统数学模型和系统运行状态的一致性。用广义残差方程来观测系统的残差，通过设计合适的传递函数，使得残差与未知输入(故障)解耦。当无故障时，未知输入为零，系统的输入输出与系统数学模型一致，广义残差超出预计的统计阈值。当故障发生时，系统的广义残差超出预设的统计阈值。由于传递函数已经对未知输入进行了解耦，因此可以通过对残差的分析来分离故障。
2.2 基于知识的方法
基于解析模型的方法要求有一个精确的定量数学模型。对于大型的工业生产系统，这样的模型可能无法得到，但是现场工作的专家和操作工程师可以提供许多过程的定性描述，这些定性描述加上从过程机理得到的深层次知识，形成了基于知识的方法，如专家系统、神经网络、因果分析等。这些方法，需要一个定性的模型，通过对系统的定性描述来进行故障诊断。
2.2.1 专家系统
专家系统是基于知识的技术，是对人类思维方式的功能模拟。它将专家的经验以规则的形式用公式表达出来，这些规则可以与系统的机理描述相结合，对系统的运行状态进行逻辑推理从而达到故障诊断的目的。专家系统的基本组成包括知识库、推理机和人机接口。知识库可以含有浅知识和深知识，前者是启发性知识和专家论述，后者是根据对象的结构、机理获得深层次知识。这些知识的表示方案有产生式规则、框架、语义网络。推理机利用知识库和用户信息按照一定的推理策略进行推理，对系统的运行状态做出结论，推理机的设计应考虑推理方法、推理策略和搜索方向。人机界面是用户和专家系统进行交互的窗口，将用户信息转化为计算机语言，将系统结论转化为用户可认知的形式。
2.2.2 人工神经网络
人工神经网络是近年来发展起来的一门交叉学科，是对人脑的生理模拟，它能够描述复杂的非线性关系。神经网络在用于故障检测与诊断时，常用的做法是：过程变量作为人工神经网络的输入层，输出层的每个神经元分别对应着不同类型的已知故障，用已知的过程数据对神经元网络进行训练，描述过程的正常状态和故障状态。在理论上，人工神经网络可以完美地描述系统行为，但是由于过程的复杂性，人工神经网络在进行训练时往往会遇到较大的困难。
2.2.3 因果分析法
因果分析法使用的是故障症状关系的因果模型，有符号定向陶(signed directed graph，SDG)和症状树模型方法(symptom tree model，STM)。SDG是一种显示过程变量间因果关系的图，它反映了过程的特性及系统的拓扑结构，使用SDG进行故障诊断的目标是，通过观察到的症状，定位代表系统故障的根节点。基本的SDG存在一些缺陷，对其改进后可以更好地进行故障诊断，STM与SDG相似，是一种将故障与症状关联起来的故障树模型的实时形式，在STM中，故障的根本原因是通过求取隶属于所观察症状的各种原凶的交叉点来确定的。
2.2.4 模糊理论
模糊理论是1965年Zadeh提出的，它是处理广泛存在的不确定、模糊时间的理论工具，为复杂系统的故障诊断提供了重要的理论方法。模糊逻辑系统的优点是一个适当设计的模糊逻辑系统可以在任意精度上逼近某个给定的非向性甬数。利用专家知识米构造模糊规则库，可以充分利用专家系统的推理规则。本文转载自http://www.biyezuopin.vip/onews.asp?id=6971模糊理论和人工神经网络相结合，构成模糊神经网络用于故障诊断。模糊神经元与人工神经元相似，其特别之处在于它的部分参数或者全部参数通过模糊逻辑进行描述。

% demo_LFDA.m
%
% (c) Masashi Sugiyama, Department of Compter Science, Tokyo Institute of Technology, Japan.
%     sugi@cs.titech.ac.jp,     http://sugiyama-www.cs.titech.ac.jp/~sugi/software/LFDA/

clear all;

rand('state',0);
randn('state',0);

%%%%%%%%%%%%%%%%%%%%%% Generating data
n1a=100;
n1b=100;
n2=100;
X1a=[randn(2,n1a).*repmat([1;2],[1 n1a])+repmat([-6;0],[1 n1a])];
X1b=[randn(2,n1b).*repmat([1;2],[1 n1b])+repmat([ 6;0],[1 n1b])];
X2= [randn(2,n2 ).*repmat([1;2],[1 n2 ])+repmat([ 0;0],[1 n2 ])];
X=[X1a X1b X2];
Y=[ones(n1a+n1b,1);2*ones(n2,1)];


%%%%%%%%%%%%%%%%%%%%%% Computing LFDA solution
[T,Z]=LFDA(X,Y,1);


%%%%%%%%%%%%%%%%%%%%%% Displaying original 2D data
figure(1)
clf
hold on

set(gca,'FontName','Helvetica')
set(gca,'FontSize',12)
h=plot([-T(1) T(1)]*100,[-T(2) T(2)]*100,'k-','LineWidth',2);
legend('LFDA subspace',1)
h=plot(X(1,Y==1),X(2,Y==1),'bo');
h=plot(X(1,Y==2),X(2,Y==2),'rx');
axis equal
axis([-10 10 -10 10])
title('Original 2D data and subspace found by LFDA')

set(gcf,'PaperUnits','centimeters');
set(gcf,'PaperPosition',[0 0 12 12]);
print -depsc original_data


%%%%%%%%%%%%%%%%%%%%%% Displaying projected data
figure(2)
clf

subplot(2,1,1)
hold on
set(gca,'FontName','Helvetica')
set(gca,'FontSize',12)
hist(Z(Y==1),linspace(min(Z),max(Z),20));
h=get(gca,'Children');
set(h,'FaceColor','b')
axis([min(Z) max(Z) 0 inf])
title('Data projected onto 1D LFDA subspace')

subplot(2,1,2)
hold on
set(gca,'FontName','Helvetica')
set(gca,'FontSize',12)
hist(Z(Y==2),linspace(min(Z),max(Z),20));
h=get(gca,'Children');
set(h,'FaceColor','r')
axis([min(Z) max(Z) 0 inf])

set(gcf,'PaperUnits','centimeters');
set(gcf,'PaperPosition',[0 0 12 12]);
print -depsc projected_data_LFDA


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73