BP算法学习心得（反向传播算法）

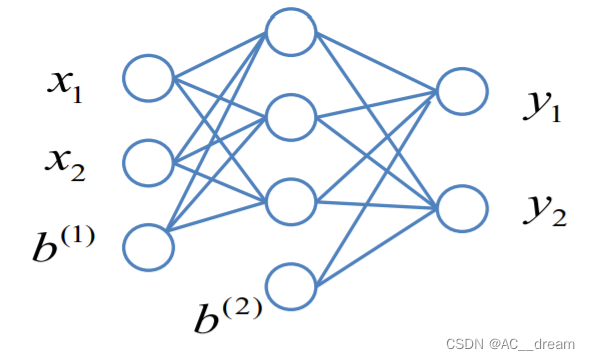
以此图为例：x1和x2代表两个输入，b(1)代表一个偏置常数。每条边代表一个权重，现在我们可以通过给定的输入代入可以计算得到输出y1和y2，但是实际输出和我们的真实值可能存在一定的误差，BP算法就是一种用来修正这种误差的算法，通过输出值来修改每一层的权值参数从而减少误差。

我们要优化的误差函数形式如下：

由多元泰勒展开式可以得到

我们为了使这个值减少，我们可以直接取wij的变化量为其前面系数的相反值，这样我们就可以使得误差减少。这也就是梯度下降法，所以问题就转化为怎样求误差关于w的偏导数。

注意，这里我们可以发现在上面这个图中只有两类w，一类是输出层的w，另一类是中间层的w，我们分别以这两种w中的其中一个进行公式推导即可，目的是为了找到误差函数J和w之间的关系。

 通过对输出层的w求导后可以发现，偏导数只与这条边的两个节点有关系，就等于前一个节点的输出值乘以后一个节点的误差再乘以后一个节点的激活函数的导数在该输出的值。

同理很容易得到J对其他输出层参数w的偏导数

这是对隐含层w的求偏导结果。这个稍微复杂一些，因为这个要用两次链式法则才能够求出结果。

利用上面两类公式即可完成参数w的更新。

BP算法的原理就是利用梯度下降来更新权值w从而减少误差，通过一次次的迭代使得误差尽可能地小，每次都是沿每个w的梯度负方向更新w，直至损失函数取得最小值。

BP算法的缺陷：

首先我们可以发现BP算法是利用梯度下降法实现的，所以他肯定具有梯度下降法所具有的一些缺陷，比如容易求得局部最小值，解决方法就是通过多初始化几次参数来求得极小值中的最小值即可。

通过求J对隐含层的w偏导数我们可以发现，里面需要连续两次使用链式法则，那么我们不难想到，如果神经元的层数足够多，就会多次使用链式法则，那么就会导致我们的权值呈指数级增长或者下降，这取决于指数是大于1还是小于1。也就是容易出现梯度消失和梯度爆炸问题。

如果训练次数过多，还容易产生过拟合问题。