想要精通算法和SQL的成长之路 - 打家劫舍系列问题

前言

想要精通算法和SQL的成长之路 - 系列导航

一. 打家劫舍

原题链接
你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。 给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

• 输入：[1,2,3,1]
• 输出：4
• 解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。

我们规定dp[i]：为到第i天为止，能偷到的最大金额。

• 如果今天要偷，说明昨天（肯定没偷）或者前几天没偷：dp[i] = dp[i-1] + num[i] = dp[i-2] + num[i]
• 如果今天不偷：dp[i] = dp[i-1]

因此：

dp[i] = Math.max(dp[i-2] + num[i], dp[i-1])
1

那么确定了递归公式之后，我们需要考虑动态规划数组的初始值了。考虑到上面的i-2，因此我们需要考虑两个初始变量。

• dp[0] ：也就是第一天的最大利润是多少，肯定是偷了才有利润：dp[0] = num[0]
• dp[1]：最大利润：要么第一天偷，要么第二天偷，取两者最高。dp[1] = max (num[0],num[1])

那么最终结果如下：

public int rob(int[] nums) {
    int len = nums.length;
    // 特判
    if (len == 0) {
        return 0;
    }
    if (len == 1) {
        return nums[0];
    }
    // 初始化
    int[] dp = new int[len];
    dp[0] = nums[0];
    dp[1] = Math.max(nums[0], nums[1]);
    // 递归
    for (int i = 2; i < len; i++) {
        dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1]);
    }
    return dp[len - 1];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

二. 打家劫舍II(环形限制)

原题链接

在第一题的基础上：房屋都围成了一圈。那么相比第一题，就要多思考几个点：

• 在偷最后一个房屋的时候，第一个房屋是否偷过？

比如我有5个房子：[A，B，C，D，E], 那么面临的选择就是以下几种：（首尾最多选择一种）

• 情况一：A不偷，E可能偷。
• 情况一：A可能偷，E不偷。

那么也就是在第一题的情况下做出选择：

• 情况一：利用第一题的代码，传入的数组去掉头。
• 情况一：利用第一题的代码，传入的数组去掉尾。

代码就是：

public int rob(int[] nums) {
    int len = nums.length;
    // 特判
    if (len == 0) {
        return 0;
    }
    if (len == 1) {
        return nums[0];
    }
    if (len == 2) {
        return Math.max(nums[0], nums[1]);
    }
    // 情况一：第一家肯定不偷
    int res1 = robOne(Arrays.copyOfRange(nums, 1, len));
    // 情况二：最后一家肯定不偷
    int res2 = robOne(Arrays.copyOfRange(nums, 0, len - 1));
    return Math.max(res1, res2);
}
// 第一题代码
public int robOne(int[] nums) {
    int len = nums.length;
    // 初始化
    int[] dp = new int[len];
    dp[0] = nums[0];
    dp[1] = Math.max(nums[0], nums[1]);
    // 递归
    for (int i = 2; i < len; i++) {
        dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1]);
    }
    return dp[len - 1];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

三. 打家劫舍III(二叉树限制)

原题链接

第三题呢则是在第一题的基础上，将数组房屋改造成了一个二叉树：即相邻的两个节点也是不能够偷的。

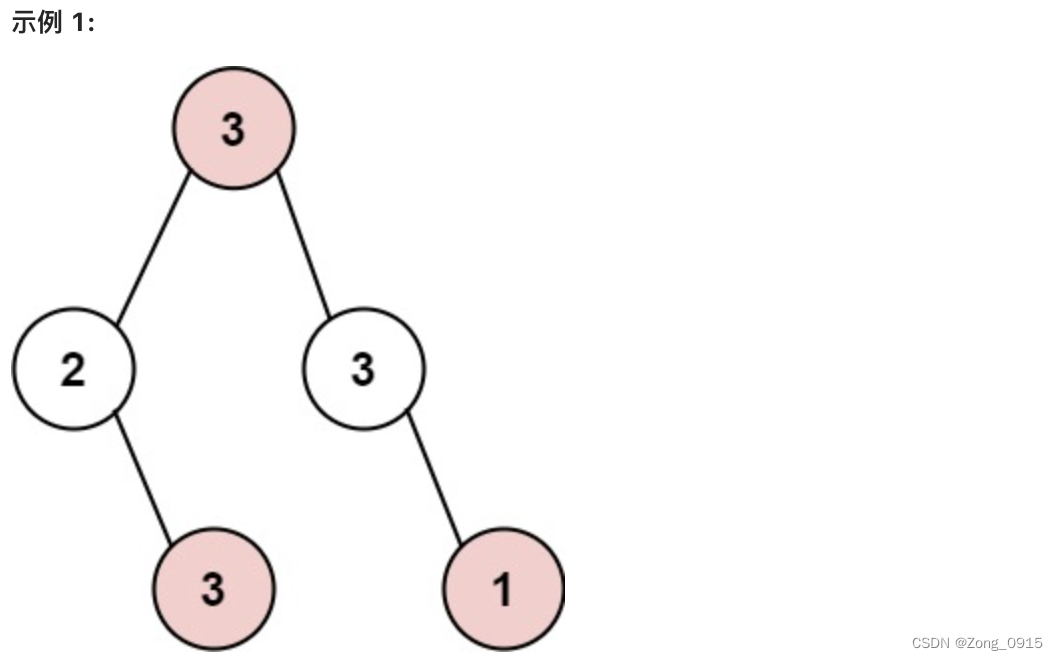
• 输入: root = [3,2,3,null,3,null,1]
• 输出: 7
• 解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7

这个题目由于搞成了二叉树结构，那么就跟原本的数组结构天差地别。

假设dp[node][i]代表以node为根节点时，能取到的最大利润值。i有两种值：0代表不偷当前节点，1代表偷当前节点。我们需要考虑的就是：

• 如果当前节点偷，那么当前节点的子节点不能够偷。
• 如果当前节点不能偷，那么当前节点能够获取到的最大利润：取以下两种情况的最大值：左节点的最大利润，右节点的最大利润值。

那么我们就需要自底向上推算根节点root能够获取的最大利润。

我们写一个递归函数，他返回一个int[]类型的数组，即：

public int[] dfs(TreeNode node) {

}
1
2
3

他代表以node为根节点时，返回一个数组大小为2的最大利润集：分别为当偷当前节点和不偷当前节点时候的最大利润。

---

那么首先，对于递归函数的终止条件，这个简单明了：

if (node == null) {
    return new int[]{0, 0};
}
1
2
3

其次我们拿到当前根节点的左右孩子的最大利润集合：

int[] left = dfs(node.left);
int[] right = dfs(node.right);
1
2

以左孩子为例，left集合代表着如下含义：

• 以node.left为根节点，并且偷node.left的最大利润。
• 以node.left为根节点，并且不偷node.left的最大利润。

那么接下来的，就应该写最大利润是怎么获得的：分为两种情况：

• 不偷当前节点，那么左右子树可偷可不偷，分别取最大值然后相加：dp[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1])
• 偷当前节点，那么左右子树都不能给偷，左右子树最大利润此时即left[0]和right[0]：dp[1] = node.val + left[0] + right[0];

int[] dp = new int[2];
dp[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
dp[1] = node.val + left[0] + right[0];
return dp;
1
2
3
4

最终代码就是：

public int rob(TreeNode root) {
    int[] res = dfs(root);
    return Math.max(res[0], res[1]);
}

public int[] dfs(TreeNode node) {
    if (node == null) {
        return new int[]{0, 0};
    }

    // 以左孩子为根节点时，取到的 两种 最大利润可能。
    int[] left = dfs(node.left);
    // 以右孩子为根节点时，取到的 两种 最大利润可能。
    int[] right = dfs(node.right);

    int[] dp = new int[2];
    // 以node为根节点时能够获取的最大利润，并且当前节点不偷。
    // 那么左右孩子都可以偷，因此当前节点的最大利润为两个孩子的最大利润之和
    dp[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
    // 以node为根节点时能够获取的最大利润，并且当前节点偷
    // 那么当前节点偷了的话，它的左右孩子肯定是不能够偷的，根据 相邻不能偷 的原则
    // 那么这种情况下以左孩子为例，左孩子肯定是不能够偷的，那么它的最大利润就是left[0]
    dp[1] = node.val + left[0] + right[0];
    return dp;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25