-
leetcode动态规划系列(求路径篇)
目录
1、 不同路径
题目描述:

思路:看到路径直接就不多想就是动态规划,这道题是给定我们目标的坐标m和n,要我们求机器人能到达目标坐标的路径有多少条,机器人只能往下或者往右走一步,所以这个关系我们很容易找啊,dp[i][j] = dp[i-1][j] + dp[i][j-1] ,就是一个位置的可能路径就是左边位置+上面位置;
找到这个关系我们思路就很清晰了,直接上代码:
- public int uniquePaths(int m, int n) {
- int[][] dp = new int[m][n];
- for (int i = 0; i < m; i++) dp[i][0] = 1;
- for (int i = 0; i < n; i++) dp[0][i] = 1;
- for (int i = 1; i < m; i++) {
- for (int j = 1; j < n; j++)
- dp[i][j] = dp[i-1][j] + dp[i][j-1];
- }
- return dp[m-1][n-1];
- }
此时时间复杂度O(m*n),空间复杂度O(m*n)
我们会发现,我们虽然用了一个二维数组来dp,但是只用了一次,我们为什么要浪费这么大的空间呢,完全可以转化为一个一维数组,dp[i] = dp[i] + dp[i-1]

用一个一维数组代替原来的二维数组,极大程度的减少了我们耗费的空间!
我们进入代码:
- public int uniquePaths(int m, int n) {
- //把pre[j]=cur[j]
- int[] dp = new int[n];
- Arrays.fill(dp,1);
- for (int i = 1; i < m; i++) {
- for (int j = 1; j < n; j++)
- dp[j] += dp[j-1];
- }
- return dp[n-1];
- }
优化后的空间复杂度:O(m)
2、最小路径和
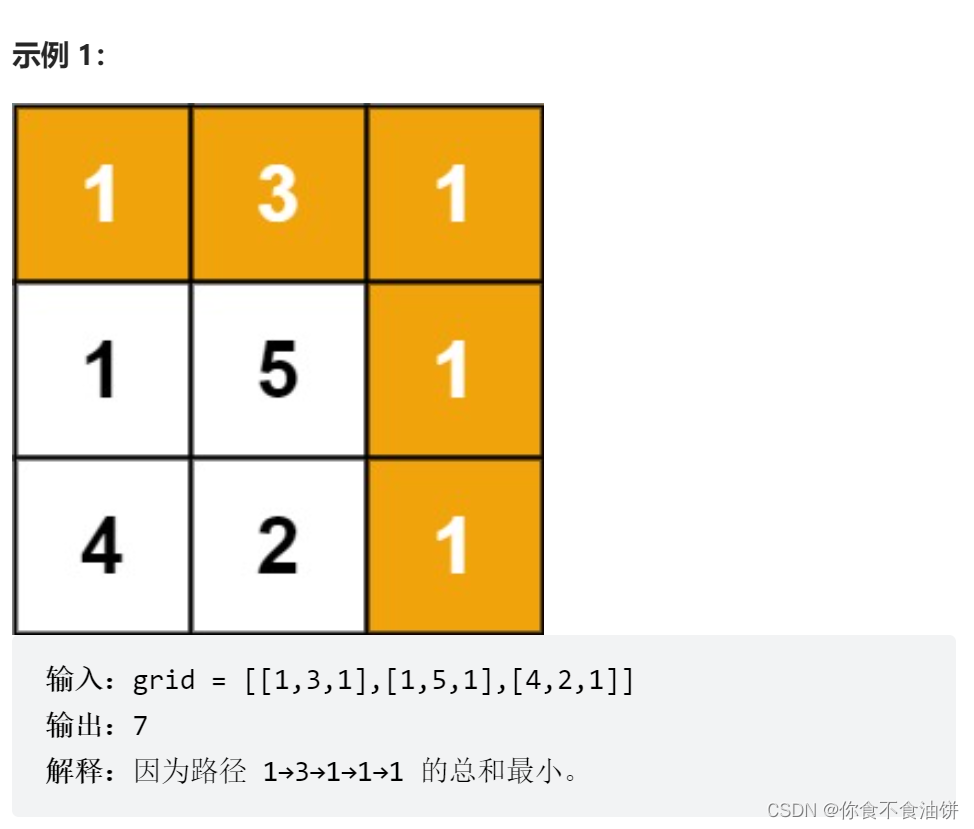
思路:老规矩,先确定解题方法,求路径用动态规划,这道题与咱们上一道讲解的不同路径和有点相似,大家可以先自己根据上一题的思路想想这道题;
咱们言归正传,先审题,这道题要我们求从左上角到右下角的最小路径和,关键点来了规定只能向下或者向右走一步,所以我们找最小路径和时,只需要比较上面位置的路径和左边位置的路径,即求dp[i][j] = grid[i][j] + Math.min(dp[i-1][j],dp[i][j-1]);
注:由于题目给定我们的是二维数组,我们可以不引入新的数组,可以直接在原来的数组grid上进行动态规划
我们直接进入代码:
- public int minPathSum(int[][] grid) {
- for (int i = 0; i < grid.length; i++) {
- for (int j = 0; j < grid[0].length; j++) {
- if (i == 0 && j == 0) continue;
- else if (j == 0) grid[i][j] += grid[i-1][j];
- else if (i == 0) grid[i][j] += grid[i][j-1];
- else grid[i][j] += Math.min(grid[i-1][j],grid[i][j-1]);
- }
- }
- return grid[grid.length-1][grid[0].length-1];
- }
时间复杂度:O(m*n)
空间复杂度:O(1)
持续更新中~~
-
相关阅读:
PostgreSQL 在WAL文件中查找drop table、update、delete操作
关于微信二次分享,自定义分享参数不生效问题
学生HTML个人网页作业作品:HTML绿色的化妆品静态网站(web前端网页制作课作业)
js添加 删除 替换 插入节点所用的方法。js常用的几种事件。
idea-java: 错误: 无效的源发行版:16
使用.NET简单实现一个Redis的高性能克隆版(二)
LeetCode 1114 按序打印
C#中的四种类型转换
Flume学习笔记
【工程实践】CatBoost进行多分类
- 原文地址:https://blog.csdn.net/weixin_72076848/article/details/126122614