信号与线性系统分析（吴大正，郭宝龙）（5-系统定义与典型系统）

前言

我发现，信号与系统中有一些东西真的是反复会在别的工科专业中用到，所以在这里记录一下，虽然有视频，但是视频毕竟比较长，想要快速回顾，需要从头看视频，所以这里记录一下比较关键的东西。

视频地址：信号与线性系统分析（吴大正，郭宝龙）。

系统定义

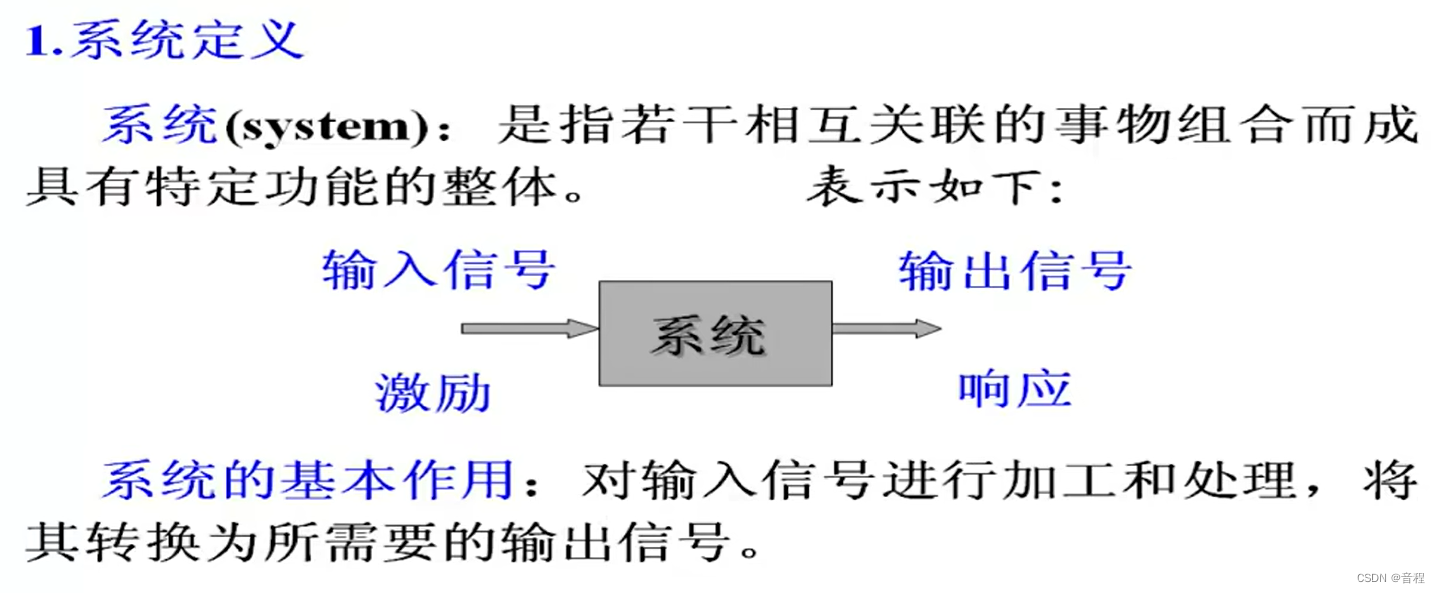
上面这个很好理解

这个（2系统模型）不是很好理解，和物理比较相关，这里跳过。我们看3。系统的状态，这里解释一下，根据上一张图，我们很容易会认为系统就是一个函数而已，将输入映射为输出。现在这个3告诉我们，不是的，相当于系统有记忆了，有状态，比如你是一个高手，老师告诉你一个知识，你输出了理解，反之，你是一个小白，你输出了听不懂。高手，小白就是两种状态。反映到物理当中，可以理解为系统中有一些原件，比如电容器可以存储电荷，具有记忆功能，称之为状态。

常见系统分类

线性系统

动态系统

f表示输入，x表示状态。既然有状态的概念，所以，上面那2个响应都是针对动态系统定义的，而不是即时系统。

zs:zero state;zi:zero input。

不过，话说回来，好像即时系统可以看成零状态响应的动态系统。

动态线性系统

第一个说一下，即系统的相应可以分解为对状态的响应和对输入的响应。类似于算法中解耦合，这样子就简单多了。

下面给出了一个例子，注意，状态是x(0),输入是f(x)，然后对这两个东西作用，变换的东西叫做系统。

时变与时不变系统

为什么叫做时不变呢？可以这么理解，任意时刻输入，得到的输出都是不变的（只是一个时间延迟而已）。

上面这个怎么证明？视频里好像没有给出证明，我自己小证明了一下微分特性，就是根据定义，写出导数定义式，然后由于其线性性质，可以得到。至于积分，即可以看成求和，由于线性性质，好像也可以得到。这算是一个初步的理解吧，因为我没有用到时不变性质就证明了上述，不知道有没有问题。

因果与非因果系统

这个看起来很奇怪，就是说，因果系统要满足输出必须在输入之后或者同时出现。上面一个非因果系统，即t=1的时候，系统就得到了t=2时候的输入。

例题

下面做一个题目，不算难，只是符号看得有点眼花缭乱。

注意，上面那个是中括号，不是绝对值。