【2022】CMKT: Concept Map Driven Knowledge Tracing概念图驱动的知识追踪

摘要

在本文中，我们提出并提出了一种新的概念图驱动的知识追踪模型(CMKT)，该模型利用教育概念图对学习者建模。这篇文章特别解决了学习者一方不愿意练习和不规律的学习行为所导致的学习者数据稀疏的问题。CMKT将概念图作为一种新的信息源，明确地利用其固有信息来帮助估计学习者的知识状态。具体而言，概念图中的成对教育关系被表述为排序对，并用作模型构建的数学约束。利用网络嵌入技术提取拓扑信息，并将其作为模型输入。CMKT结合了概念图中的教育关系信息和拓扑信息，采用递归神经网络执行知识追踪任务。对四个不同学科的五个公共教育数据集(超过8000名学习者和他们的30万份记录)进行的综合评价证明了CMKT的前景和有效性:ROC曲线下平均面积(AUC)和总体预测精度(ACC)分别达到0.82和0.75,CMKT在AUC和ACC方面至少优于所有基线12.2%和9.2%。

1 引言

在教育领域，知识追踪(KT)是指通过定量诊断学习者在个别教学概念(如数学中的“分数”或“线性方程”)上的掌握水平，对学习者的知识状态进行建模。KT的结果可以直接用来估计学习者目前的知识优势和劣势，它已经服务于各种智能辅导系统(ITS)和计算机支持的教育环境[2]。此外，KT及其分析结果已被用于当今的在线学习平台，包括大规模在线开放课程[3]，为学习资源和模块[4]提供个性化推荐。

传统的KT主要利用学习者的练习和学习活动数据来构建模型，并据此估计学习者的知识状态。ITS和mooc的快速发展为以实用和廉价的方式收集这些数据提供了良好的平台。然而，它也遇到了一个主要的挑战:学习者的练习和学习活动数据的稀疏性。具体来说，学习者使用在线教育系统的时间往往不规律，花在练习或复习个人概念以及综合评估[5]上的时间较少。对于每个个体学习者来说，很可能只有目标学科或课程中的一小部分概念得到了实践(即通过解答测验问题)或复习(即通过浏览教程视频或与导师互动)。因此，这类学习者对大部分概念的掌握信息很可能是未知的，这使得KT模型表现不佳，并在其他应用中受到限制，包括学习者学习成绩预测[6]、问题难度估计[7]和学习路径适应[8]。

然而，将任何严格的学习或练习程序强加给学习者以收集必要和充分的KT信息是不切实际和不公平的。其他处理数据稀疏的策略，如数据增强[9]和迁移学习[10]，由于人类在知识领域的认知过程的复杂性，也难以在KT中应用。因此，我们对解决这个数据稀疏性问题的关键取决于来自知识领域本身的信息。具体而言，我们提出并提倡使用概念图[11]，充分利用其固有信息来帮助KT模型的构建。简单地说，概念图是指通过联系来说明概念之间不同的教育关系的教育学概念的图形表示。**教育领域成熟的知识空间理论[12]揭示了客观领域知识中的教学概念与主观学习者认知过程之间的天然依赖关系。**根据知识空间理论，人类的学习过程建模可以利用从概念图中得到的信息。图1给出了一个简化的概念图，它由六个具有前提关系的概念(即从C1到C6)组成。将概念图信息引入知识状态估计中，为KT模型的构建提供了数据来源，有助于缓解数据稀疏性。在教育领域，特别是在K-12教育领域，大多数学科和课程的概念图都是由领域专家或经验丰富的教师构建的，可以直接用于教学或研究目的。

一般来说，概念图中的两类信息有助于知识状态估计，可用于KT模型:1)教育关系信息和2)拓扑信息。概念图中的教育关系主要是指教学概念之间隐含的但具有教育意义的依赖关系，通常用于优化学习和教学过程。以一种被称为先决关系的教育关系为例。鉴于一些概念是另一个概念的先决条件(例如，“加法”和“乘法”是数学中“因式分解”的先决条件)，如果一个学习者掌握了后一个概念(即“因式分解”)，就可以推断该学习者很可能已经掌握了它的先决条件(即“加法”和“乘法”)。除了前提关系之外，许多其他关系类型，如包含关系、因果关系和递进关系，也出现在不同的概念图中。另一方面，拓扑信息主要是指概念图的物理结构，它表明每个概念是如何与其他概念联系在一起的，以及它在整个地图结构中的位置。例如，如图1所示，给定一个概念在概念图中处于中心位置(如“加法”和“乘法”是概念“因式分解”的先决条件，“因式分解”是概念“线性方程”和“平方根”的先决条件)，这个概念(如“因式分解”)将比位于地图边缘的其他概念更为关键和重要。教育关系信息和概念图中的拓扑信息都可以集成到KT模型中，以便更好地估计知识状态。

本文通过在KT模型设计中引入概念图信息来解决这些问题。特别地，我们设计了一个新的KT模型，该模型显式地集成了教育关系信息和从概念图派生的拓扑信息。在构建所需的KT模型时，存在几个关键的技术挑战。例如，如何将定性的成对教育关系恰当地表述为定量的数学形式，然后与KT模型进行整合，就不是一件简单的事情。此外，概念图自然形成有向无环图(DAG)，这使得常用的针对泛图的网络嵌入方法不适合[13]。因此，有效地从概念图中提取拓扑信息并将其与KT模型集成并不是一项简单的任务。为了解决这些挑战，我们考虑将成对教育关系转换为特定的数学约束，以正则化学习者状态估计。我们还探索了一种新的嵌入方法来学习概念图的拓扑信息，这些信息可以作为新的KT模型的附加输入

---

因此，本文的主要贡献有以下几点：

• 新的KT模型设计**:为了缓解学习者数据稀疏性的问题，更好地建模学习者，我们提出了一个新的KT模型，利用概念图的固有信息。**
• 教育关系建模**:为了正确地使用概念图中的教育关系，我们将其成对关系建模，通常是先决条件关系，作为排序对，然后将它们用作新的KT模型构建的数学约束。**
• 拓扑信息嵌入:为了直接使用概念图中的拓扑信息，我们使用网络嵌入技术来提取所需的信息。嵌入结果作为KT模型的新输入。
• 多数据集和综合评价:利用4个学科的5个公共教育数据集(8000多名学习者和30万份记录)，我们对提出的模型进行了综合实验，结果表明，新的KT模型在ROC曲线下平均面积(AUC)和总体预测精度(ACC)方面分别比所有基线至少提高了12.2%和9.2%

虽然提出的新模型是新颖和有效的，但我们相信本文的关键影响是强调了使用领域知识及其固有信息对学习者建模的更广泛的可能性，并最终使学习者和他们的学习过程能够更好地建模、分析和预测。

2 KT和学习者模型

KT主要用于评估学习者个体的知识状态。现有的KT模型往往将特定概念或技能的知识状态作为潜在变量，并试图根据从学习者收集到的连续练习表现来估计掌握概率。我们以建立的贝叶斯KT (BKT)[1]作为一个例子。给定同一学习单元(概念或技能)的若干问题，以及学习者在这些问题上的练习表现(是否正确回答)，BKT模型旨在及时估计学习者是否掌握了该学习单元。具体来说，BKT模型假设一个潜在的二元变量作为学习者的知识状态，即掌握和不掌握，给定学习者对一系列问题的练习结果，及时更新学习者对学习单元的掌握概率。在实际应用中，BKT模型通常采用贝叶斯规则计算后验概率。此外，观察到的学习者的练习结果取决于潜在的知识状态，因此，所建立的BKT模型可用于预测学习者未来的学习表现，并为学习者设计干预(或推荐)策略。
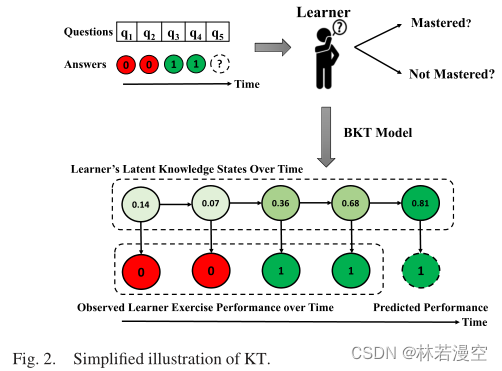
图2通过一个简化的例子说明了BKT模型是如何工作的。如果一个学习者在同一个学习单元上，答错了前两个问题，然后又答对了后面两个问题，那么BKT模型会先降低其知识状态的掌握概率(即从0.14降到0.07)，然后再考虑下面两个正确答案，逐步提高掌握概率。最后，该模型还可以预测学习者将正确回答第五个问题，对该概念的掌握概率很高(即0.81)。除了传统的BKT模型外，近年来研究者尝试将深度学习模型应用到深度KT (DKT)模型[14]中，利用序列学习练习数据训练循环神经网络(RNN)对学习者的潜在知识状态进行建模。

3 问题定义

4

要求_{R1表明，如果一个概念以高概率被掌握，那么它的前提概念将以更高的概率被掌握。另一方面，需求}R2表明，如果一个先决条件的概念以较低的概率被掌握，那么成对的概念将以更低的概率被掌握。

许多类型的教育关系，如先决条件和包容，都是方向性的，没有任何循环，因此，相应的概念图自然形成DAG。这种DAG特性使得典型的基于随机漫步的网络嵌入算法如Deepwalk[24]和LINE[25]不适合。这一特性也导致为链结构设计的标准RNN模型也不适合。受之前的dagu相关研究[26]、[27]的启发，我们利用GRU体系结构，提出了一种新的DAGGRU网络来学习概念的嵌入，从而获取概念图的拓扑信息。

C、建模拓扑信息
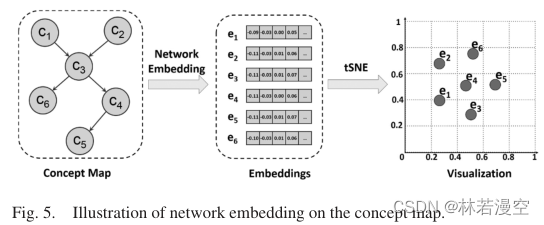
如前所述，概念图的拓扑信息指的是它的物理结构，它提供了相互关联的概念的全局依赖信息。为了将图数据转化为低维空间并最大限度地保留其拓扑信息，网络嵌入[22]是一种自然而有效的方法。我们仍然以图1所示的简化概念图为例。图5为网络嵌入结果，即e1到e6的6个多维向量。为了更好地可视化这些向量，我们采用T分布随机邻居嵌入(T - sne)[23]将其降尺度到二维空间中，在二维空间中我们可以很容易地看到嵌入结果的拓扑信息。例如，给定概念c4和c6共享相同的前提概念c3，我们可以看到它们的嵌入e4和e6在图5的二维空间中相互接近。

许多类型的教育关系，如先决条件和包容，都是有向的，没有任何循环，因此，相应的概念图自然形成DAG。这种DAG特性使得典型的基于随机漫步的网络嵌入算法如Deepwalk[24]和LINE[25]不适合。这一特性也导致为链结构设计的标准RNN模型也不适合。受之前的dagu相关研究[26]、[27]的启发，我们利用GRU体系结构，提出了一种新的DAGGRU网络来学习概念的嵌入，从而获取概念图的拓扑信息。

5 实验

在本节中，我们首先介绍实验设置，包括评估数据集、基线和设置。然后，我们评估了提出的CMKT模型，并将其与基线模型进行比较。最后通过实验说明了重要参数的影响。

实验设置

1）数据集
数据集:为了充分评估CMKT模型，我们在四个学科中使用了五个不同的公共教育数据集，即ASSIST、AICFE-CM、AICFE-GE、AICFE-MA和AICFE-PH。具体来说，ASSIST指的是公共数据集ASSISTment 2009-20101[30]，该数据集通常用于KT和其他相关的教育数据挖掘研究。

其他所有四个“AICFE-*”数据集都来自一个名为“智能学习者伙伴”(SLP)的在线教育平台，该平台由北京师范大学未来教育先进创新中心(AICFE)开发和维护。SLP平台目前服务于北京135所当地学校的6万多名学生，主要是7年级到9年级的学生。特别是，AICFE-CM、AICFE-GE、AICFE-MA和AICFEPH数据集分别涉及化学、地理、数学和物理等学科，这些数据集也可在网上用于研究3。

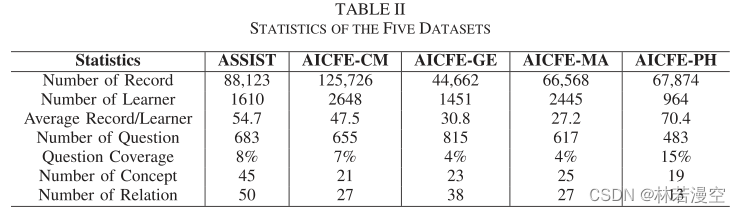
对于ASSISTment数据，我们在数学中使用它的“非技能构建器”数据集，并应用特定的过滤操作对该数据集进行预处理。我们首先选择“随机顺序”生成的序列，而不是“线性顺序”生成的序列，因为“随机顺序”序列可以避免强加顺序可能带来的偏差。然后，我们选择长度大于30的序列，以确保学习者方面有足够的信息。我们最后使用的问题是检查主题中概念的一个子集。请两位领域专家手工标记前提关系，得到的Kappa值为0.83。表II的第一列给出了用于实验的ASSIST数据集的详细统计信息。对于AICFE数据集，我们还使用检查主题中概念子集的问题，并且对于每个主题，两个领域专家手动标记了先决条件关系。

表二也给出了实验中AICFE数据集的详细统计数据。在表II中，第三行“平均记录/学习者”显示了每个学习者在数据集中的平均练习记录数量，范围从27.2到70.4，这表明数据集捕获了所有学习者必要的练习信息。第五行“问题覆盖率”是用上面的“平均记录/学习者”除以问题数计算出来的，问题数大致描述了每个学习者回答问题的百分比。数据集的低覆盖率值在4%到15%之间，这在一定程度上说明了当今ITS和MOOC平台严重的数据稀疏性，如引言部分所述。

2）基线:四个现有的KT模型被用作基线，即BKT[33]，概率矩阵分解(PMF) [34]， DKT[14]，和GKT [35]: BKT -正如前面所描述的，BKT利用二元变量来建模概念掌握。基于给定概念上的练习序列，它本质上利用隐马尔可夫模型(HMM)来更新二进制变量的概率。BKT模型固有地假设掌握的知识不会被遗忘，但考虑了猜测和滑移等因素。BKT是一个经典的已建立的模型，被广泛用于不同的KT任务。

PMF - PMF技术是最近被用来解决KT问题[34]的，而PMF技术最初是为推荐系统设计的。它本质上是将问答问题转化为相似度比较问题，学习者在一个问题上的表现取决于她的知识状态与问题之间的相似度。具体而言，PMF将学习者的知识状态和问题作为潜在向量进行建模，并将它们投射到同一个空间中计算相似度，最终预测学习者的表现。

DKT-DKT是第一个使用深度学习技术和RNN结构的KT模型，其中采用了长短时记忆(LSTM)单元。提出的CMKT模型采用了与DKT相似的RNN结构(使用GRU而不是LSTM)，但明确且适当地从概念图中融合了教育关系信息和拓扑信息。

GKT-GKT使用图神经网络模型来追踪学习者的知识状态。通过利用给定的知识结构，GKT首先通过聚合邻近概念状态来计算概念的新掌握状态，然后根据计算出的状态更新邻近状态。因此，GKT估计了学习者对所有概念的知识状态。

CMKT- c -除了这四个基线模型之外，我们还构建了CMKT模型，其中没有包含概念图的拓扑信息(即输入向量上没有嵌入概念)，并将其称为CMKT- c模型。所有其他部分，包括其GRU结构和源自教育关系的数学约束，都与提出的CMKT模型相同。

3）评价设置:我们从分类和回归两个角度对KT模型进行评价。将练习结果视为一个分类问题，将练习结果视为一个二元变量，0表示错误答案，1表示正确答案。因此，ROC曲线下面积(AUC)和总体预测精度(ACC)可作为模型评价的两个指标。另一方面，考虑到这是一个回归问题，将练习结果视为一个从0到1的连续变量。因此，平均绝对误差(MAE)和均方根误差(RMSE)可以作为模型评价的两个指标。在实验中，对于每个数据集，随机选取90%的数据作为训练数据，剩下的10%作为测试数据。我们重复实验10次，并报告所有四个指标的平均结果。

对于CMKT和CMKT- c模型，我们将它们的GRU隐藏状态大小设置为32，权衡参数?到0.1。参数选择过程和采用不同值的影响将在V-C节中说明。如前所述，模型训练采用Adam优化算法，初始学习率设置为0.01，迭代次数设置为500。该模型在Linux服务器上使用Tensorflow在Python中实现，该服务器包含128 GB RAM，两个Intel Xeon Processor E5-2683 v3 cpu和一个GeForce GTX TITAN X GPU。

B 评估结果

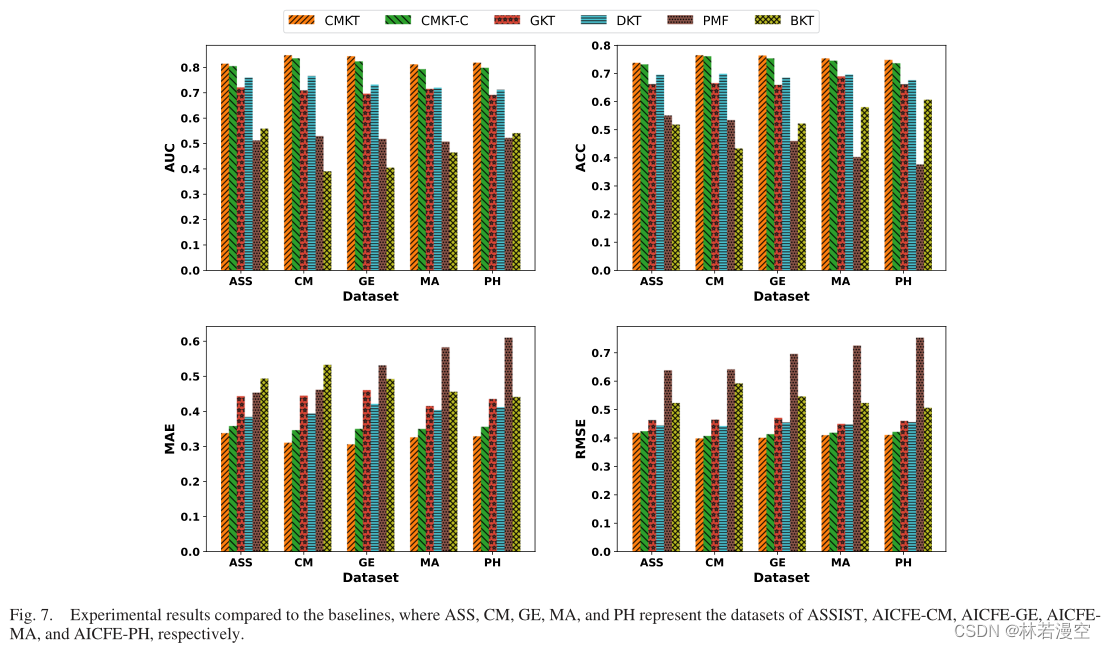
图7显示了在所有五个数据集上的四个指标，即AUC、ACC、MAE和RMSE的评估结果。

首先，与其他现有模型相比，CMKT和CMKT- c模型在所有数据集上都获得了较高的AUC和ACC，以及较低的MAE和RMSE。具体而言，在5个数据集上，CMKT的平均AUC、ACC、MAE和RMSE分别为0.82、0.75、0.32和0.41。与基线模型相比，CMKT在AUC和ACC上至少增加了12.2%和9.2%，在MAE和RMSE上至少减少了19.7%和9.1%。这些结果验证了来自概念图的信息显著提高了估计学习者对KT问题的知识状态的准确性。其次，CMKT模型在所有关键指标上的表现都优于CMKT- c模型，这表明概念图中的拓扑信息和提出的DAG-GRU嵌入方法有效地提高了模型的性能。第三，基线模型PMF和BKT在不同的数据集上表现出不一致的性能。

例如，PMF在ASSIST和AICFECM数据集上的性能优于BKT，而BKT在其他数据集上的性能更好。

相比之下，CMKT、CMKT- c、DKT和GKT模型在所有5个数据集上的表现更加一致，这意味着基于深度学习的模型可能具有更强的鲁棒性。第四，将所有数据集上的AUC和ACC与MAE和RMSE进行比较，结果与分类和回归指标一致。

为了进一步观察模型在不同水平的学习者练习数据下的表现，我们对50%、60%、70%和80%的训练数据进行了实验，其余的进行测试。图8显示了性能的变化。

训练样本的不同百分比，其中采用五个数据集上的四个指标进行评估。从图8中，我们可以看到，在所有五个数据集和四个指标上，随着训练规模的增加，CMKT模型的性能不断提高。

6 结论

在本文中，我们提出了CMKT模型，利用概念图来解决学习者数据稀疏性问题，然后对学习者的知识状态进行更准确的估计。我们首先从概念图中建立教育关系模型，作为排序对和数学约束，构建模型目标函数。然后提出了概念嵌入技术，将概念图中的拓扑信息嵌入到模型中。实验结果表明，该模型的AUC和ACC分别达到0.82和0.75，在这五个数据集上分别提高了所有基线12.2%和9.2%。

在更广泛的范围内，提出的CMKT模型展示了使用来自领域知识的信息建模人类认知过程的好处。也就是说，它部分地说明了人类的知识状态与领域知识客观结构的自然依赖性密切相关，这与知识空间理论是一致的。我们相信，许多新颖的学习模型，包括但不限于KT模型，都可以使用类似的设计理念得到启发和实现，这最终将推动信息技术系统以及教育领域的其他智能平台的发展。