【ACWing】1401. 围住奶牛

题目地址：

https://www.acwing.com/problem/content/description/1403/

农夫约翰想要建造一个围栏来围住奶牛。构建这个围栏时，必须将若干个奶牛们喜爱的地点都包含在围栏内。现在给定这些地点的具体坐标，请你求出将这些地点都包含在内的围栏的最短长度是多少。注意：围栏边上的点也算处于围栏内部。

输入格式：
第一行包含整数$N$，表示奶牛们喜爱的地点数目。
接下来$N$行，每行包含两个实数$X_i,Y_i$，表示一个地点的具体坐标。

输出格式：
输出一个实数，表示围栏最短长度。保留两位小数。

数据范围：
$0\le N\le 10000$
$-10^6\le X_i,Y_i\le 10^6$
数据保证所有奶牛不会全部处在同一条直线上。

其实就是求这些点的凸包的周长，可以用Andrew算法。先将所有点排序，先按$x$坐标从小到大排，如果$x$相等则按$y$坐标从小到大排。排好之后开一个栈，然后遍历所有的点，如图：

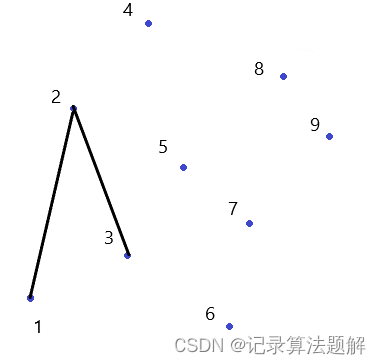
我们希望沿着顺时针方向，从点$1$开始，先搞定点$1$和点$N$连线的上半部分的点，然后再搞定下半平面的点。开始的两个点默认入栈，接下来每次遍历下一个点$p$的时候，就看一下当前栈顶的两个元素$p_1,p_2$（这里$p_2$是栈顶，$p_1$是栈顶下面的元素）和当前点，如果向量$\overrightarrow{p_1{p}_2}$和$\overrightarrow{p_{1}p}$满足右手定则（此时$p_1\to p_2\to p$是凹下去的，不凸），则我们需要将栈顶丢弃，一直到不满足右手为止，然后将这个点入栈。要判断满不满足右手定则，可以算一下叉积$\overrightarrow{p_1{p}_2}\times \overrightarrow{p_{1}p}$（当然这两个向量是二维向量，算不了叉积，我们真正算的是将这两个向量放到三维空间的时候的叉积，并且我们只关注$z$坐标，如果$z$坐标为正，则满足右手定则）。遍历完所有点之后也就搞定了上半部分，这时候我们倒着遍历所有点，略过用过的点（除了第一个点，这个点不能略过，因为凸包要做成一个闭合折线），同时也是按上面的法则判断。这样栈里的所有点就是凸包上的点了，除了第一个点出现了两次以外。求周长是很容易的。代码如下：

#include 
#include 
#include 
#define x first
#define y second
using namespace std;
using PDD = pair<double, double>;

const int N = 10010;
int n;
PDD q[N];
int stk[N];
// used[i]表示下标i的点是否用过
bool used[N];

double get_dist(PDD a, PDD b) {
  double dx = a.x - b.x, dy = a.y - b.y;
  return sqrt(dx * dx + dy * dy);
}

PDD operator-(PDD &a, PDD &b) {
  return {a.x - b.x, a.y - b.y};
}

double cross(PDD a, PDD b) {
  return a.x * b.y - a.y * b.x;
}

double area(PDD a, PDD b, PDD c) {
  return cross(b - a, c - a);
}

double andrew() {
  int top = 0;
  for (int i = 0; i < n; i++) {
    // 形成右手系了，就出栈
    while (top >= 2 && area(q[stk[top - 2]], q[stk[top - 1]], q[i]) >= 0)
      used[stk[--top]] = false;
    stk[top++] = i;
    used[i] = true;
  }

  used[0] = false;
  for (int i = n - 1; i >= 0; i--) {
    if (used[i]) continue;
    while (top >= 2 && area(q[stk[top - 2]], q[stk[top - 1]], q[i]) >= 0)
      top--;
    stk[top++] = i;
  }

  double res = 0;
  for (int i = 1; i < top; i++)
    res += get_dist(q[stk[i - 1]], q[stk[i]]);

  return res;
}

int main() {
  scanf("%d", &n);
  for (int i = 0; i < n; i++) scanf("%lf%lf", &q[i].x, &q[i].y);
  // 排序并去重
  sort(q, q + n);
  int idx = 1;
  for (int i = 1; i < n; i++) if (q[i] != q[idx - 1]) q[idx++] = q[i];
  n = idx;
  printf("%.2lf\n", andrew());
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

时间复杂度$O(n\log n)$，空间$O(n)$。