搜索技术【深度优先搜索】 - m 叉树

搜索技术【深度优先搜索】 - m 叉树

给定无向连通图G 和m 种颜色，找出所有不同的着色方案，使相邻的区域有不同的颜色。

如果把地图上的每一个区域都退化成一个点，将相邻的区域用线连接起来，地图就变成了一个无向连通图，给地图着色相当于给该无向连通图的每个点都着色，要求有连线的点不能有相同的颜色，这就是图的m 着色问题。

【举个栗子】

该地图共有7个区域，分别是A、B、C、D、E、F、G，按上面的顺序编号1～7，对每个区域都用一个节点表示，相邻的区域有连线，地图就转化成了一个无向连通图，如下图所示。

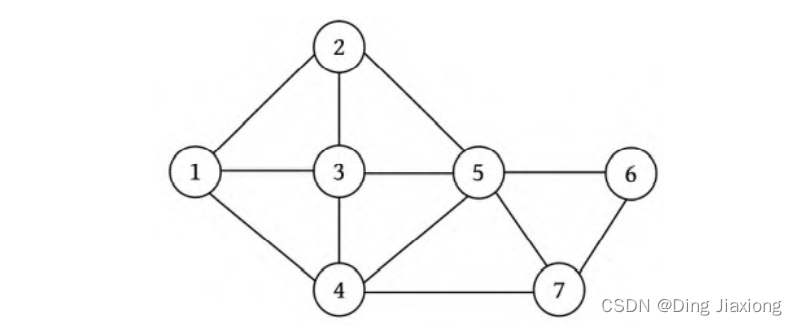
如果用3种颜色给该地图着色，那么该问题中每个节点所着的颜色均有3种选择，7个节点所着的颜色号组合是一个可能解，例如{1,2,3,2,1,2,3}。

每个节点都有m 种选择，即在解空间树中每个节点都有m 个分支，称之为m 叉树。

【算法设计】

① 定义问题的解空间

定义问题的解空间及其组织结构是很容易的。

图的m 着色问题的解空间形式为n 元组{x 1 ,x 2 ,…,xi ,…,xn }，每一个分量的取值都为1,2,…,m ，即问题的解是一个n 元向量。由此可得，问题的解空间为{x 1 ,x 2 ,…，xi ,…,xn }，其中显约束xi =1,2,…,m （i=1,2,3,…,）。xi =2表示在图G 中将第i 个节点着色为2号色。

② 确定解空间的组织结构

问题的解空间组织结构是一棵满m 叉树，树的深度为n ，如下图所示。

③ 搜索解空间

[1] 约束条件。假设当前扩展节点处于解空间树的第t 层，那么从第1个节点到第t -1个节点的状态（着色的色号）已经确定。接下来沿着扩展节点的第1个分支进行扩展，此时需要判断第t 个节点的着色情况。第t 个节点的颜色要与前t -1个节点中与其有边相连的节点颜色不同，如果有颜色相同的，则第t 个节点不能用这个色号，换下一个色号尝试，如下图所示。

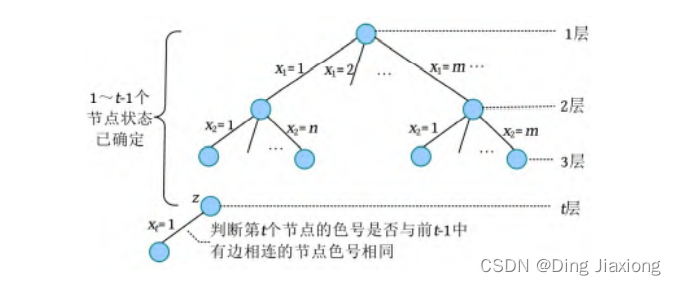
例如，假设当前扩展节点z 在第4层，则说明前3个节点的色号已经确定，如下图所示。

在前3个已着色的节点中，节点4与节点1、3有边相连，那么节点4的色号不可以与节点1、3的色号相同。

[2] 限界条件。因为只找可行解就可以了，不是求最优解，因此不需要限界条件。

[3] 搜索过程。扩展节点沿着第1个分支扩展，判断约束条件，如果满足，则进入深一层继续搜索；如果不满足，则扩展生成的节点被剪掉，换下一个色号尝试。如果所有的色号都尝试完毕，则该节点变成死节点，向上回溯到离其最近的活节点，继续搜索。搜索到叶子节点时，找到一种着色方案。搜索到全部活节点都变成死节点时为止。

【举个栗子】

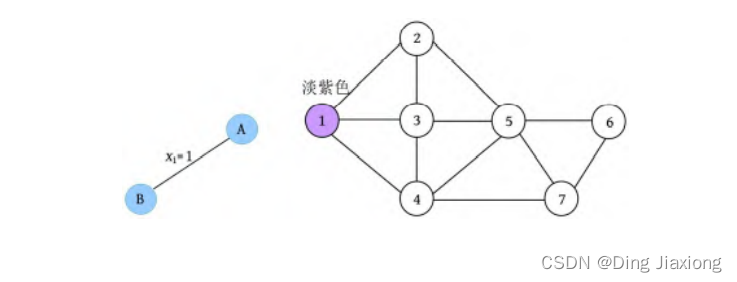
地图的７个区域转化成的无向连通图如下图所示。如果现在用3种颜色（淡紫、茶色、水绿色）给该地图着色，那么该问题中每个节点所着的颜色均有3种选择（m =3），7个节点所着的颜色组合是一个可能解。

[1] 开始搜索第1层（t =1）。扩展节点A的第1个分支，首先判断是否满足约束条件，因为之前还未着色任何节点，所以满足约束条件。然后扩展该分支，令节点1着1号色（淡紫），即x [1]=1，生成节点B。搜索过程和着色方案如下图所示。

[2] 扩展节点B（t =2）。扩展第1个分支x [2]=1，首先判断节点2是否与前面已确定色号的节点（1号）有边相连且色号相同，不满足约束条件，剪掉该分支。然后沿着x [2]=2扩展，节点2与前面已确定色号的节点（1号）有边相连但色号不相同，满足约束条件，扩展该分支，令节点2着2号色（茶色），即x [2]=2，生成节点C。搜索过程和着色方案如下图所示。

[3] 扩展节点C（t =3）。扩展第1个分支x [3]=1，首先判断节点3是否与前面已确定的节点（1、2号）有边相连且色号相同，节点3与节点1有边相连且色号相同，不满足约束条件，剪掉该分支。然后沿着x[3]=2扩展，节点3与前面已确定色号的节点（节点2）有边相连且色号相同，不满足约束条件，剪掉该分支。然后沿着x [3]=3扩展，节点3与前面已确定色号的节点（节点1、2）有边相连且色号均不相同，满足约束条件，扩展该分支，令节点3着3号色（水绿色），即令x [3]=3。生成节点D。搜索过程和着色方案如下图所示。

[4] 扩展节点D（t =4）。扩展第1个分支x [4]=1，首先判断节点4是否与前面已确定的节点（节点1、2、3）有边相连且色号相同，节点4和节点1有边相连且色号相同，不满足约束条件，剪掉该分支。然后沿着x [4]=2扩展，节点4与前面已确定色号的节点（节点1、3）有边相连但色号均不同，满足约束条件，扩展该分支，令节点4着2号色（茶色），令x [4]=2。生成节点E。搜索过程和着色方案如下图所示。

[5] 扩展节点E（t =5）。扩展第1个分支x [5]=1，首先判断节点5是否与前面已确定的节点（节点1、2、3、4）有边相连且色号相同，节点5与前面已确定色号的节点（节点2、3、4）有边相连但色号均不同，满足约束条件，扩展该分支，令节点5着1号色（淡紫色），令x[5]=1，生成节点F。搜索过程和着色方案如下图所示。

[6] 扩展节点F（t =6）。扩展第1个分支x [6]=1，首先判断节点6是否与前面已确定的节点（节点1、2、3、4、5）有边相连且色号相同，节点6与前面已确定色号的节点（节点5）有边相连且色号相同，不满足约束条件，剪掉该分支。然后沿着x [6]=2扩展，节点6和前面已确定色号的节点（节点5）有边相连但色号不同，满足约束条件，扩展该分支，令节点6着2号色（茶色），令x [6]=2。生成节点G。搜索过程和着色方案如下图所示。

[7] 扩展节点G（t =7）。扩展第1个分支x [7]=1，首先判断节点7是否与前面已确定的节点（节点1、2、3、4、5、6）有边相连且色号相同，节点7与前面已确定色号的节点（节点5）有边相连且色号相同，不满足约束条件，剪掉该分支。然后沿着x [7]=2扩展，节点7与前面已确定色号的节点（节点4、6）有边相连且色号相同，不满足约束条件，剪掉该分支。接着沿着x [7]=3扩展，节点7与前面已确定色号的节点（节点4、5、6）有边相连但色号不同，满足约束条件，扩展该分支，令节点7着3号色（水绿色），令x [7]=3。生成节点H。搜索过程和着色方案如下图所示。

[8] 扩展节点H（t =8）。t >n ，找到一个可行解，输出该可行解{1,2,3,2,1,2,3}。回溯到最近的活节点G。

[9] 重新扩展节点G（t =7）。节点G的m （m =3）个孩子均已考察完毕，成为死节点。回溯到最近的活节点F。

[10] 继续搜索，又找到第2种着色方案，输出该可行解{1,3,2,3,1,3,2}。搜索过程和着色方案如下图所示。

[11] 继续搜索，又找到4个可行解，分别是{2,1,3,1,2,1,3}、{2,3,1,3,2,3,1}、{3,1,2,1,3,1,2}、{3,2,1,2,3,2,1}。

【算法实现】

[1] 约束函数。假设当前扩展节点处于解空间树的第t 层，那么从第1个节点到第t -1个节点的状态（着色的色号）已经确定。接下来沿着扩展节点的第1个分支进行扩展，此时需要判断第t 个节点的着色情况。第t 个节点的颜色号要与前t -1个节点中与其有边相连的节点颜色不同，如果有一个颜色相同的，则第t 个节点不能用这个色号，换下一个色号尝试，如下图所示。

bool OK(int t){ //约束条件
	for(int j = 1; j < t ; j ++){ //依次判断前t - 1个节点(已确定色号)
		if(map[t][j]){ //如果t 与j 邻接(有边相连)
			if(x[j] == x[t]){ //判断t与 j 的色号是否相同
				return false; //有相同色号，返回false
			}
		}		
	}
	return true; // 与前t - 1个节点中与其有边相连 的节点颜色均不同，返回true
}
1
2
3
4
5
6
7
8
9
10

[2] 按约束条件搜索求解。t 表示当前扩展节点在第t 层。如果t>n ，则表示已经到达叶子，sum累计第几个着色方案，输出可行解。否则，扩展节点沿着第1个分支扩展，判断是否满足约束条件，如果满足，则进入深一层继续搜索；如果不满足，则扩展生成的节点被剪掉，换下一个色号尝试。如果所有色号都尝试完毕，则该节点变成死节点，向上回溯到离其最近的活节点，继续搜索。搜索到叶子时，找到一种着色方案。搜索到全部活节点都变成死节点为止。

void Backtrack(int t){ //搜索函数
	if(t > n){ //到达叶子，找到一个着色方案
		sum ++;
		cout << "第" << sum << "种方案：";
		for(int i = 1; i <= n ; i++){ //输出该着色方案
			cout << x[i] << " ";
		}
		cout << endl;
	}
	else{
		for(int i = 1; i <= m ; i++){ //对每个节点都尝试m 种颜色
			x[t] = i;
			if(OK(t)){
				Backtrack(t + 1);
			}
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

【算法分析】

时间复杂度： 在最坏情况下，除了最后一层，有1+m +m^2 +…+m^(n-1) = (m^n -1)/(m -1)≈m^(n -1) 个节点需要扩展，而这些节点每个都要扩展m 个分支，总的分支个数为m^n ，每个分支都判断约束函数，判断约束条件需要O (n )时间，因此耗时O (nm^n )。在叶子节点处输出可行解需要耗时O (n )，在最坏情况下会搜索到所有叶子，叶子个数为mn ，故耗时O (nm^n )。因此，时间复杂度为O (nm^n )，如下图所示。

空间复杂度： 回溯法的另一个重要特性就是在搜索执行的同时产生解空间。在搜索过程中的任何时刻，仅保留从开始节点到当前扩展节点的路径，从开始节点起最长的路径为n 。在程序中使用x []数组记录该最长路径作为可行解，所以该算法的空间复杂度为O (n )。