每日三题-有效的括号、最有效括号、最小栈

👨‍💻个人主页： 才疏学浅的木子
🙇‍♂️ 本人也在学习阶段如若发现问题，请告知非常感谢 🙇‍♂️
📒 本文来自专栏： 算法
🌈 算法类型：Hot100题 🌈
❤️ 支持我：👍点赞 🌹收藏 🤟关注

有效的括号

解法一

使用栈保存符号的左边框
如果出现有边框就与栈顶符号进行匹配
如果匹配失败则return false
注意： 对栈的使用要注意判空

class Solution {
    public boolean isValid(String s) {
        Stack<Character> stack = new Stack<Character>();
        for(int i  = 0;i < s.length();i++){
            char cur = s.charAt(i); // 当前字符
            if(cur == '[' || cur == '{' || cur == '(')stack.add(cur);
            else {
                if(stack.isEmpty()) return false; // 如果当前为空
                char t = stack.pop();
                if(cur == ']' && t != '[') return false;
                if(cur == ')' && t != '(') return false;
                if(cur == '}' && t != '{') return false;
            }
        }
        if(!stack.isEmpty()) return false;
        return true;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

最长有效括号

解法一

遍历
首先判断长度为len的字符串是否满足
然后判断长度为len-1的字符串是否满足
然后一直到判断长度为2的字符串是否满足
时间复杂度为(O(N^3))

class Solution {
    public int longestValidParentheses(String s) {
        int len = s.length();
        if(len <= 1 )return 0;
        for(int i = len-1;i >= 1;i--){ // 当前匹配字符串的长度
            for(int j = 0;j < len-i;j++){ //从哪里开始匹配
                if(isVaild(s,j,j+i)){
                    return i+1; // 因为i比长度少了1
                }
            }
        }
        return 0;
    }
    public Boolean isVaild(String s,int l,int r){
        Stack<Character> stack = new Stack<Character>();
        for(int i = l;i <= r;i++){
            if(s.charAt(i) == '(') stack.add(s.charAt(i));
            else {
                if(stack.isEmpty()) return false;
                if(stack.pop() != '(') return false; 
            }
        }
        return stack.isEmpty();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

解法二

使用栈
知世 参考这位大佬的文章

class Solution {
    public int longestValidParentheses(String s) {
        int res = 0;
        Stack<Integer> stack = new Stack<Integer>();
        int start = 0;
        for(int i = 0;i < s.length();i++){
            if(s.charAt(i) == '(') stack.add(i);
            else{
                if(stack.isEmpty()){
                    start = i+1;
                }else{
                    stack.pop();
                    if(stack.isEmpty()){  // 说明从start-i都是匹配好的
                        res = Math.max(res,i-start+1);
                    }else{ // 说明现在的s.peek()后面 - i是匹配好的
                        res = Math.max(res,i-stack.peek());
                    }
                }
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

解法三

使用动态规划
这就是一个最值问题
设置dp[i] 为以s.charAt(i)结尾的字符串的最长有效括号的长度
所以当s.charAt(i) == '('时候，dp[i] = 0
**注意：**边界问题多判断是否到-1了
所以有下面几种情况

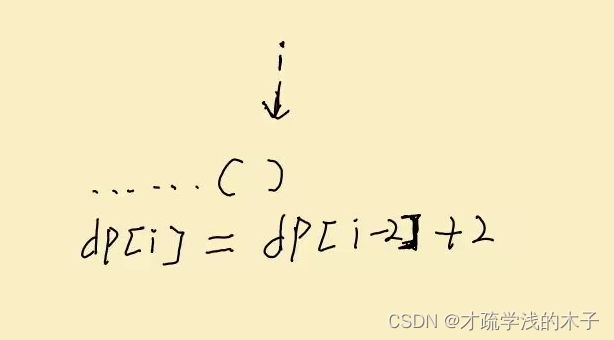
class Solution {
    public int longestValidParentheses(String s) {
        int len = s.length();
        int res = 0;
        if(len <= 1) return 0;
        int dp[] = new int[len];  //dp[i] 表示以s.charAt(i) 结尾的字符串的长度
        for(int i = 1;i < len;i++){
            //s,charAt(i) == '('则为 0 
            if(s.charAt(i) == ')'){
                if(s.charAt(i-1) == '('){ // 说明是这种情况 ()()
                    dp[i] = (i-2>=0?dp[i-2]:0) + 2;
                }else if(i-dp[i-1] > 0 && s.charAt(i-dp[i-1]-1) == '('){
                    dp[i] = 2 + dp[i-1] + (i-dp[i-1]-2 >= 0 ?dp[i-dp[i-1]-2]:0);
                }
            }
            res = Math.max(res,dp[i]);
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

解法四

使用left保存左括号的数量
使用right保存右括号的数量
如果left < right 说明右括号多了，说明这里已经与后面的断开了，后面的不会在这里以及前面的存在匹配直接left == right ==0
如果left == right，那么这时候匹配的长度就是2 * right
但是存在可能left 一直 大于right，那么这样就可以从后往前遍历解决问题

class Solution {
    public int longestValidParentheses(String s) {
        int res = 0;
        int left = 0,right = 0;
        for(int i = 0;i < s.length();i++){
            if(s.charAt(i) == '('){
                left++;
            }else{
                right++;
            }
            if(left == right){
                res = Math.max(res,2*right);
            }
            if(left < right){
                left = right = 0;
            }
        }

        left = right = 0;
        for(int i = s.length()-1;i >= 0;i--){
            if(s.charAt(i) == ')'){
                left++;
            }else{
                right++;
            }
            if(left == right){
                res = Math.max(res,2*right);
            }
            if(left < right){
                left = right = 0;
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

最小栈

解法一

额外维护一个最小栈

class MinStack {
    Stack<Integer> s1 = null;
    Stack<Integer> min = null;
    public MinStack() {
        s1 = new Stack<Integer>();
        min = new Stack<Integer>();
    }
    
    public void push(int val) {
        s1.add(val);
        if(min.isEmpty()){
            min.add(val);
        }else{
            int t = min.peek();
            min.add(t > val?val:t);
        }
    }
    
    public void pop() {
        s1.pop();
        min.pop();
    }
    
    public int top() {
        return s1.peek();
    }
    
    public int getMin() {
        return min.peek();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31