KMP模式匹配算法

一、朴素的模式匹配算法

给定字符串M和N，求M中是否包含N，如果包含，则返回N在M中的起始位置

对于上面这道题目，我们很容易就能想到如下解法：

M和N各自维护一个指针。

首先P1指针向右遍历，寻找与P2指针相同的字符

然后P2与P1同时向右移动，并一一比对所指字符是否相同

一旦遇到不相同的字符，则停止遍历。P2回到初始位置，P1则回到此轮遍历开始时的下一个位置，然后继续前面的过程。

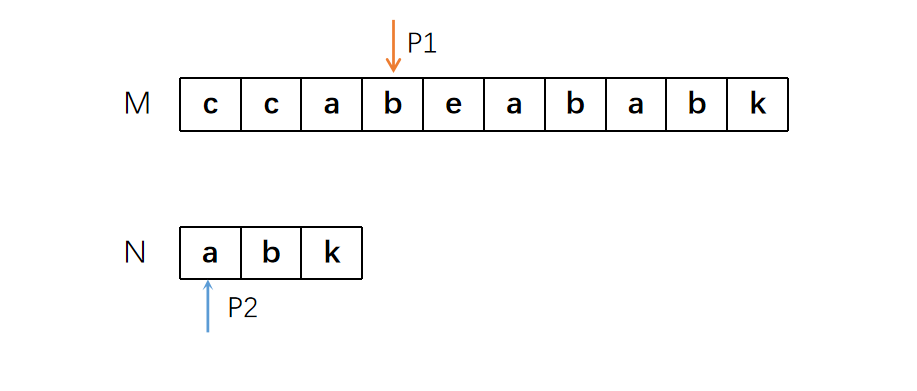
直到找到完全匹配的位置

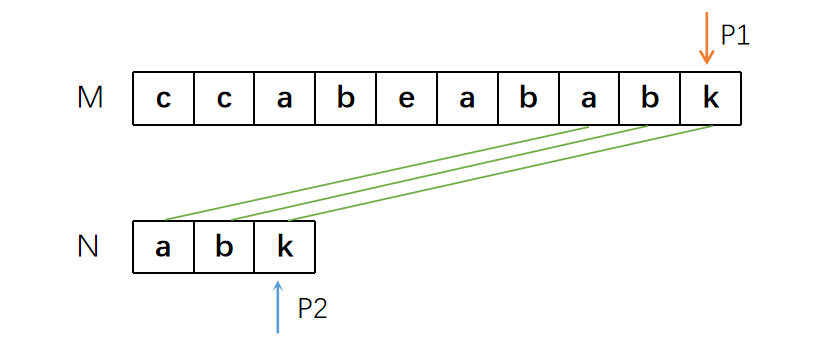
代码如下

/// 

/// 朴素的匹配模式算法
/// 
/// 
/// 
/// 
private int Process1(string m,string n)
{
	if (m == null || n == null || m.Length < n.Length || n.Length <= 0)
		return -1;
	int p1=0, p2 = 0;

	while (p1 < m.Length && p2 < n.Length)
	{
		// 两字符相同,指针共同后移
		if (m[p1] == n[p2])
		{
			p1++;
			p2++;
		}
		// 两字符不同,指针回退
		else
		{
			p1 = p1 - p2 + 1;
			p2 = 0;
		}
	}
	// 如果p2走到末尾,则匹配成功
	if (p2 == n.Length)
		return p1 - p2;
	// 否则匹配失败
	return -1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

显然这种匹配方式的效率并不高，因为每当匹配失败，都需要进行回溯并重新开始匹配。假如给定的字符串分别为M=”0000000000000000000000001“、N=”0000001“这种类型的数据，那么其时间复杂度可想而知。事实上在最差情况下，这种算法的时间复杂度会达到$O(N\times M)$级别。

二、KMP模式匹配算法

从前面的例子我们可以看出，朴素的模式匹配算法的根本问题在于：对于已经匹配过的片段没有进行记忆。

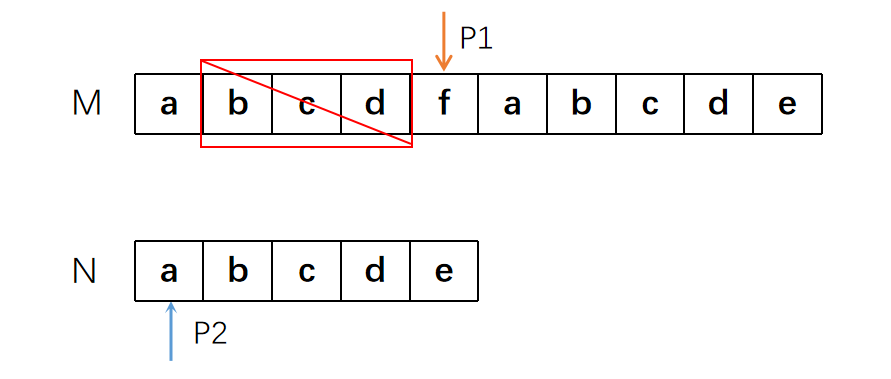
比如在进行下面的步骤时，我们首先匹配了“abcd“四个字符，到第五个字符时发现不匹配。

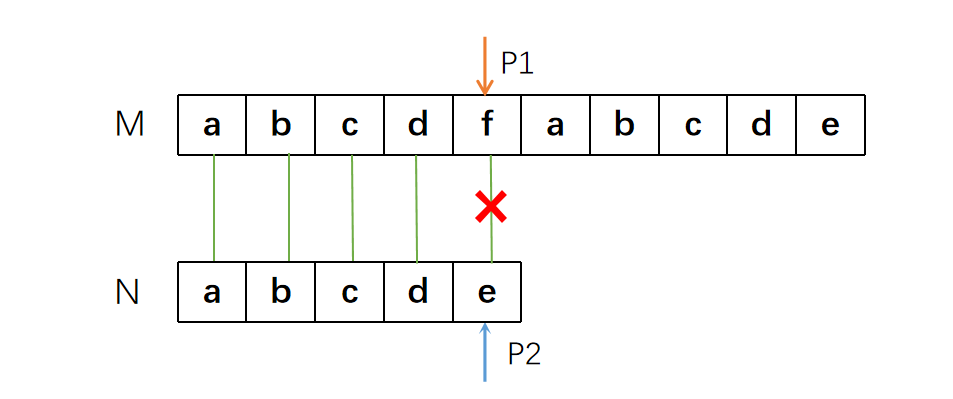
于是我们将P1指针挪回了“b”的位置，并重新开始匹配。

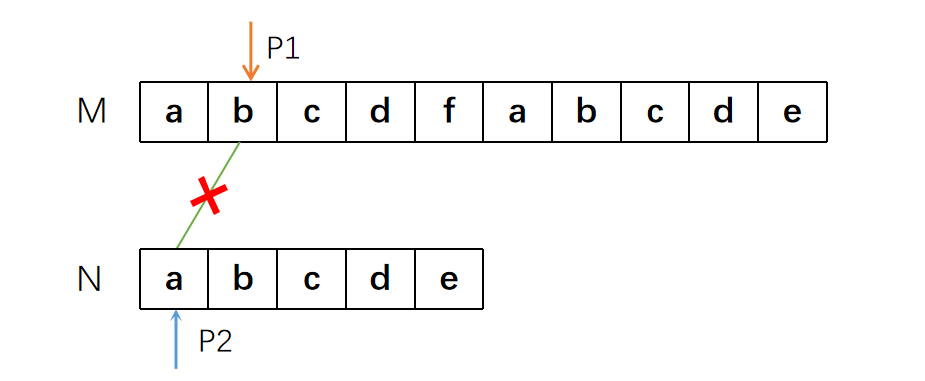
但事实上，字符串N中，没有任何一个字符与开头的“a”相同。而在上一轮匹配中，我们已经确定，所匹配内容的前四个字符是相同的。所以后面的“bcd”是一定不会匹配上N的。也就是说我们可以直接跳到“f”的位置继续进行匹配

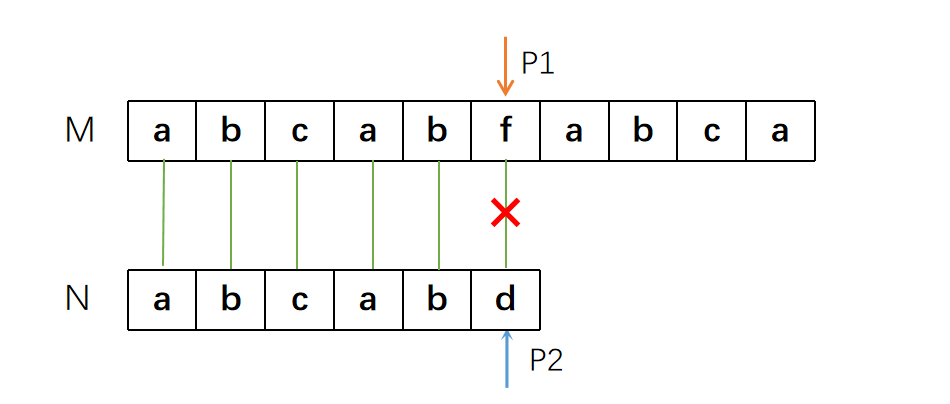
那么如果N字符串中存在相同的字符又会怎样呢？来看下面这个例子

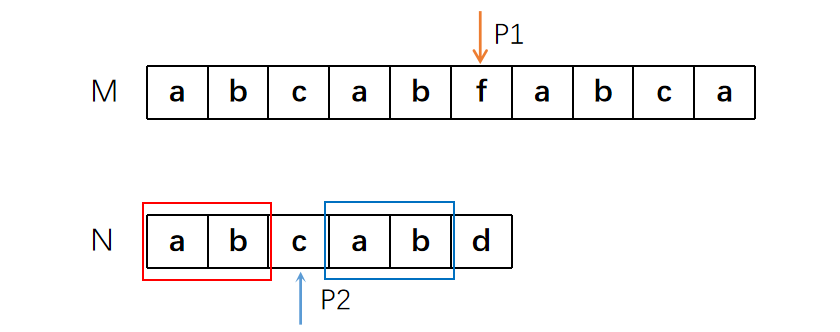
首先，当P1指针遍历到“f”字符时，匹配失败。但此时，N字符串中有与开头相同的字符“a”。也就是说，此时P1从第二个a开始匹配，是有可能匹配成功的。

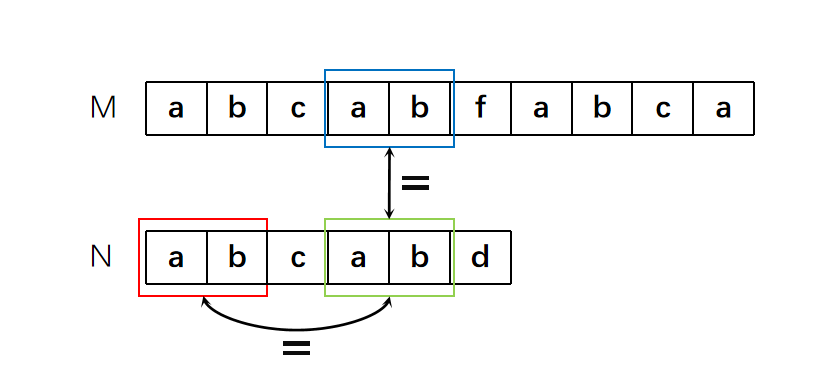
此时，我们站在上帝视角可以看出，之后的“ab”字符也是相同的，无需匹配。但在计算机视角，它在没有真正进行比较时是无法确定后面两个字符是相同的。所以我们需要证明出来。

证明起来也很简单，根据已知条件，N字符串中的红框部分和绿框部分是相同的。根据前一轮匹配可以得知，M字符串中蓝色的部分和N字符串中绿色的部分是相同的。很显然，蓝色框的部分与红色框的部分是一定相同的。

根据结论，我们又可以省下两次匹配，现在只需要在如下位置继续进行匹配就可以了

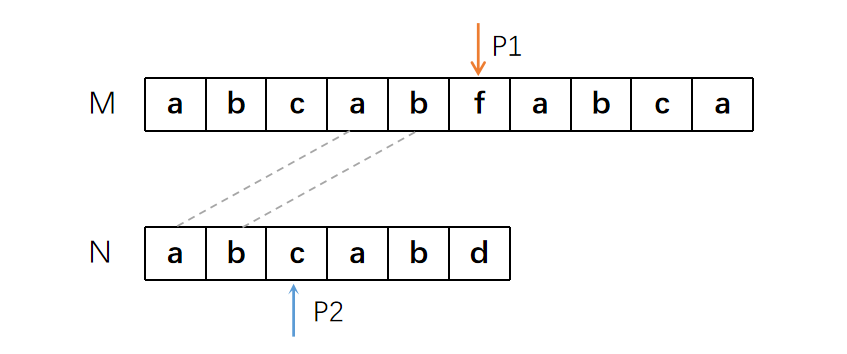
在搞清楚上面两个例子之后，我们就可以总结规律了：

• 首先，对于P1指针来说，无论上述哪种情况，都是从不相等的字符处开始匹配
• 对于P2指针的位置，主要取决于N字符串的数据情况。如果N字符串中没有重复字符，则会挪回到起始位置；如果N中有重复的字符串，就需要计算应该挪动到哪个位置。

现在问题聚焦在了“如果N存在重复字符串，P2该挪动到哪个位置”上。根据前面的例子，我们可以发现，这实际上就是求：当前匹配位置之前的字符串中，前缀与后缀相同的子串的最大长度。

可能有些难以理解，我们再通过几个例子来说明

首先是前面刚讲过的例子。此时P1与P2的字符不匹配。所以我们来求P1之前的字符串中，前缀与后缀相同的最大长度。

很显然，前后缀相同的最长子串就是“ab”，因此这个值为2。即P2挪动到下标为2的位置。

再来个极端点的例子

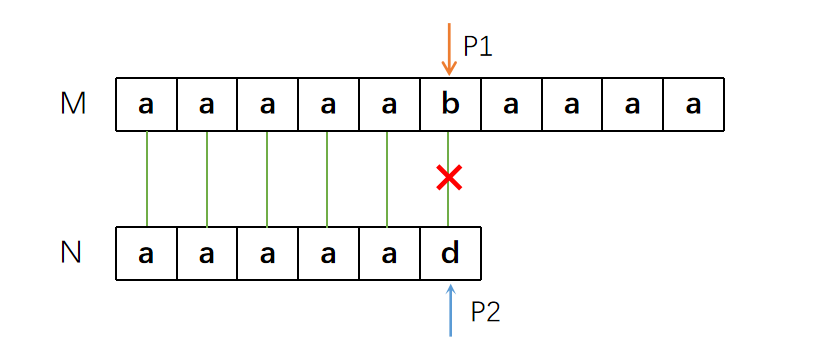
P2之前，前后缀相同的最长子串是“aaaa”，长度为4，所以P2挪动到下标为4的位置

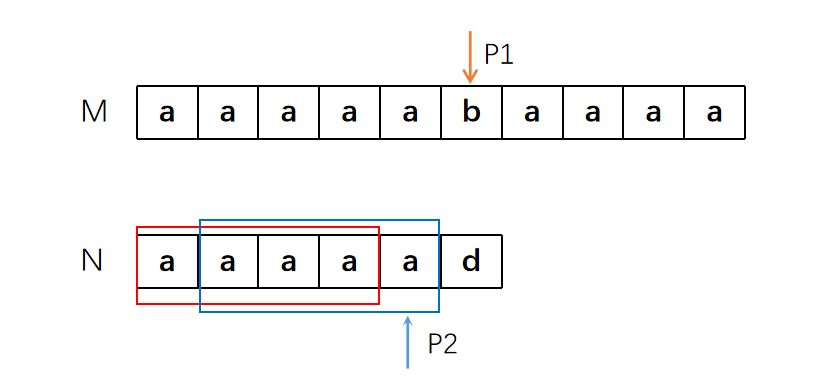
此时P1与P2仍然不相等，所以继续计算P2之前的前后缀相同最长子串的长度。结果是3，所以P2移动到下标为3的位置。

。。。。

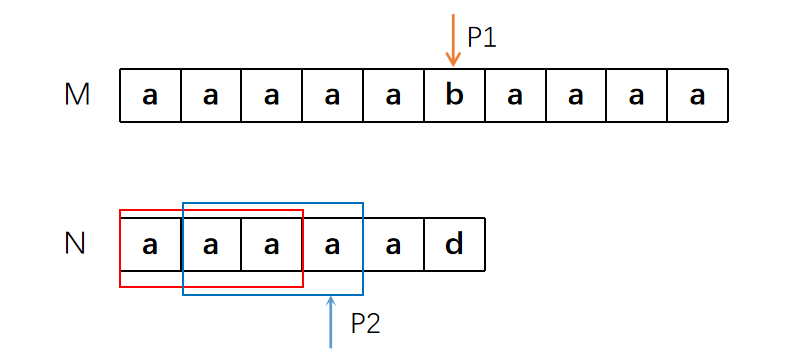
也就是说，我们需要事先计算出N字符串中，各个位置对应的前后缀相同的最长子串长度。我们把它存到一个数组中，命名为next。为了简化表达，下面的“前后缀相同的最长子串长度”统一用L表示。

那么next数组怎么求呢？还是拿具体的例子来说明

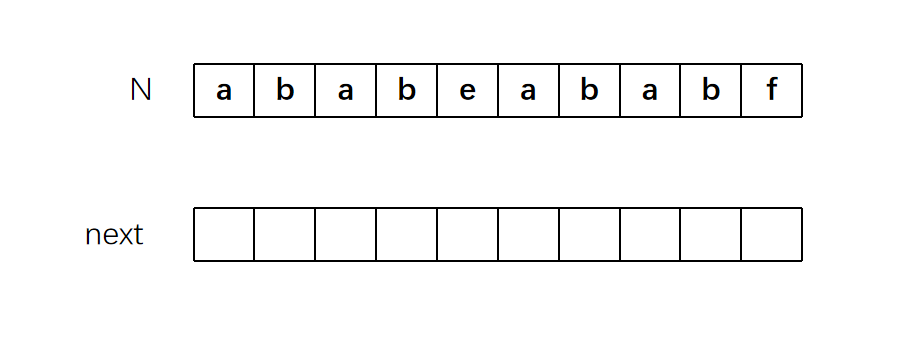
首先，next数组的第0位置是没有意义的，因为它对应的是N字符串中第0位置之前的L值，而第0位置之前是没有子串的。所以我们把它规定为-1。

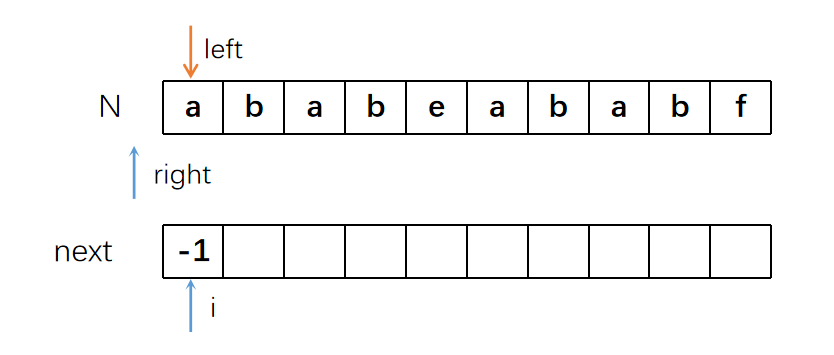
接下来right指针右移一位，来计算“b”之前的L值。但“b”之前只有一个字符“a”，所以要求的长度为0。

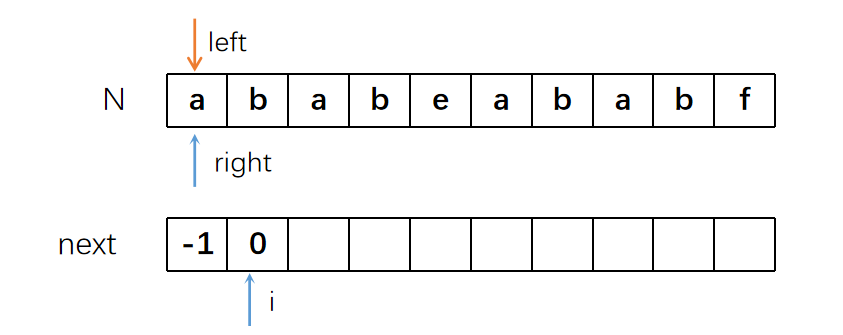
right继续右移。此时需要求“ab”字符串的L值。很显然，也是0。

right继续右移。此时要求“aba”字符串的L值。很显然，前后的“a”是相同的，所以这里的next值为1。

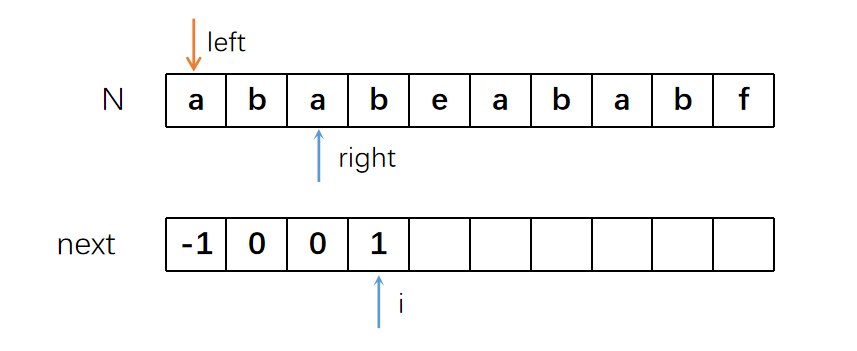
因为我们之前已经找到了一对相同的前后缀，所以left指针也要后移。意思是我们现在处于“Combo”状态，只要下一对字符仍然是相同的，说明这对相同前后缀的子串还在继续延长。如果下一对字符不同了，那我们的“Combo”状态就断了，就得重新开始匹配相同前后缀的子串了。

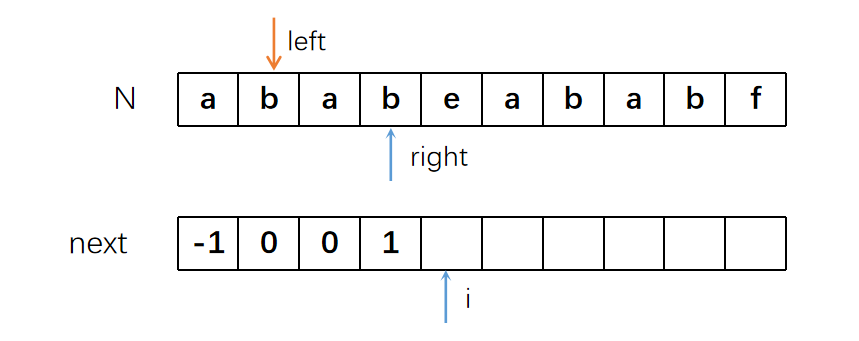
果然，此时left指针所指的字符与right所指的字符相同，也就是说L值增加到了2。

left和right指针一起右移。但这次就没这么幸运了，left和right的字符不相等了，我们的“Combo”中断了。

所以left指针要进行回溯。回溯到“Combo”之前的位置，也就是next[left]的位置。

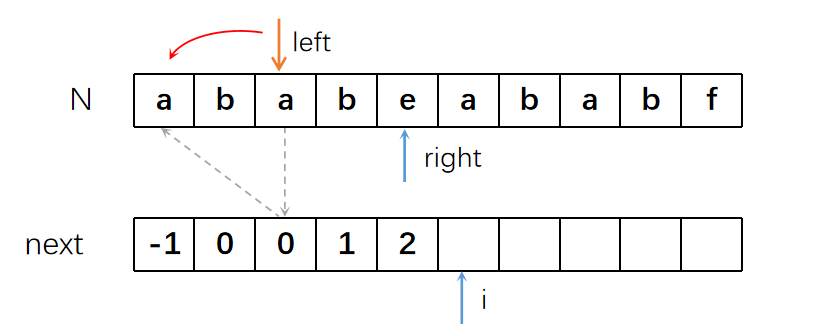
很可惜，即便left进行了回溯，也无法与right进行匹配。而且left已经无法继续向前回溯，所以L值为0。

之后的步骤与前面类似，就不再赘述了，直接上代码：

/// 

/// 获取next数组
/// 
/// 
/// 
private int[] GetNextArr(string n)
{
	int[] next = new int[n.Length];
	// 0和1位置的值是固定的
	next[0] = -1;
	next[1] = 0;
	// 定义左右指针
	int left = 0, right = 1;
	
	while (right < n.Length-1)
	{
		// 字符匹配成功时,left、right同时右移,
		// ‘前后缀相同的最长子串长度’+1(其实就是left的值)
		if (n[left] == n[right])
		{
			left++;
			next[right + 1] = left;
			right++;
		}
		// 如果匹配失败,但left还没回溯到最开始的位置,那就继续回溯
		else if (left > 0)
		{
			left = next[left];
		}
		// left回溯到0的位置也没有匹配成功,则‘前后缀相同的最长子串长度’为0
		else
		{
			next[right + 1] = 0;
			right++;
		}
	}
	return next;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

有了next数组，我们在进行匹配时，就可以按照next数组对p2指针进行回溯了。代码如下：

/// 

/// KMP算法
/// 
/// 
/// 
/// 
private int Process2(string m, string n)
{
	if (m == null || n == null || m.Length < n.Length || n.Length <= 0)
		return -1;
	int p1 = 0, p2 = 0;
	int[] next = GetNextArr(n);
	while (p1 < m.Length && p2 < n.Length)
	{
		// 如果匹配成功,两指针都后移
		if (m[p1] == n[p2])
		{
			p1++;
			p2++;
		}
		// 如果匹配失败,且p2本来就在0位置,则p1后移
		else if (p2 == 0)
		{
			p1++;
		}
		// 如果匹配失败,且p2不在0位置,则进行回溯
		else
		{
			p2 = next[p2];
		}
	}
	// p2遍历完成,说明匹配成功,否则匹配失败
	return p2 == n.Length ? p1 - p2 : -1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34