李宏毅机器学习笔记（2016年的课程）：Support Vector Machine (SVM)

目录

1. 各种loss函数

2.线性SVM

3.kernel

3.1 前言

3.2 各种 kernel

3.3 kernel VS 神经网络

---

1. 各种loss函数

f = np.arange(-3, 3 + 1e-8, 0.001)
py = np.array([1.] * len(f))
 
def get_ideal(yf):
    return np.where(yf>=0, 0, 1)
 
def square(yf):
    return np.square(yf - 1.)
 
def sigmoid(x):
    return 1. / (1 + np.exp(-x))
def square_sigmoid(yf):
    return np.square(sigmoid(yf) - 1.)
 
def cross_entropy(yf):
    return  np.log(1 + np.exp(-yf))
 
def hinge_loss(yf):
    return np.where(1 - yf > 0, 1 - yf, 0)
 
plt.plot([0] * len(f), np.linspace(-0.2, 3.2, len(f)), color='black', linewidth=0.75)
plt.plot(py*f, get_ideal(py*f), label='ideal', color='black')
plt.plot(py * f, square(py*f), label='square', color='red')
plt.plot(py * f, square_sigmoid(py*f), label='square_sigmoid', color='blue')
plt.plot(py * f, cross_entropy(py * f) / np.log(2), label='cross_entropy', color='green')
plt.plot(py * f, hinge_loss(py * f), label='hinge_loss', color='purple')

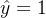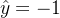这一课是讲SVM的，所以正例  ，负例  ，用 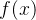 表示模型的输出。纵轴表示损失函数，横轴表示  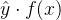 ，绘图如下：

 若是分开两种标签对模型输出绘图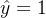，  和上图一样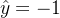，  如下图所示：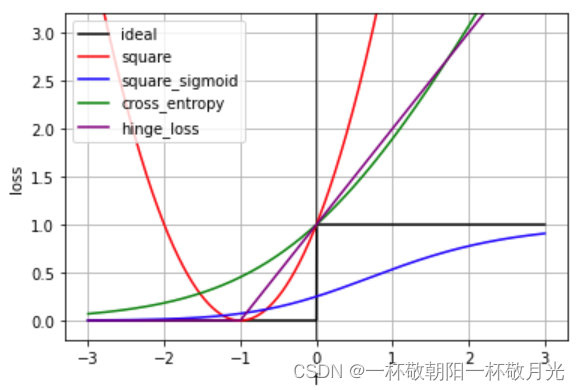

 a.黑色的线表示理想状态的损失函数，当模型输出大于0的时候最终输出1，小于0的时候最终输出-1，统计最终输出和标签不同的样本的数目，单个样本表示见上图 黑色 的 “ideal”  图例

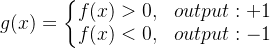
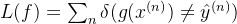
但是这个函数无法用梯度下降求解，梯度见下图，在所有可微的点其梯度均为0。我们无法直接优化它，所以用 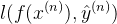 来近似 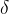 函数，这个 loss function 长啥样就随我们自己定义了。总体来说，我们期待正例的时候  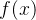越正越好，负例的时候  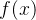越负越好，换种表示的话也可以理解为  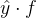越正越好。理想状况，相乘是负数得到的 loss 就是1，反之相乘同号的话 loss 就是0。

b.平方损失，我们期待，正例的时候模型输出越接近1越好，负例的时候模型输出越接近-1越好。换言之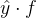，  越接近1越好。见上图 红色 的图例 “square” 。公式表示如下：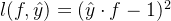

但是，这个函数是不合理的，我们不希望 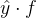 乘起来很大的时候会有很大的 loss 。

c.sigmoid + square loss ，我们期待，正例的时候 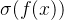 接近1，负例的时候  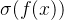接近0。见上图 蓝色 的图例 “square_sigmoid” 。公式表示如下：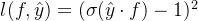

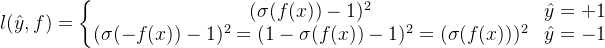
但是我们如果使用了 sigmoid 函数，通常不会使用平方损失做损失函数。因为这样不好训练，具体的见梯度图，例如当时正例的时候，模型的输出在很大的负数的地方梯度也很小，也就是说在很大的负数（并不是我们真正想要的结果）的地方参数更新的会很慢，对于很 负 的值模型没有很大的动力去调整，因为调整了之后对 loss 的影响也不是很大，这一点可以与 cross entropy 对应起来看， cross entropy 在负的很大的地方调整会对 loss 有比较大的影响，所以模型会有动力去调整，这一点也可以参见 cross entropy 的梯度图。

c.cross entropy，我们在使用了 sigmoid 函数之后，通常会使用 cross_entropy 做损失函数。见上图 绿色 的图例 “cross_entropy” ，这边除以了 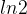 ，可以让它变成 ideal loss 的 upper bound 。公式表示如下：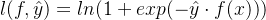

d.hinge loss ，与 cross entropy 不同的是，我们不会在输出前接 sigmoid 函数，而是直接套 hinge loss，正例的时候只要模型输出大于1损失函数就是0，负例的时候只要模型输出小于-1的时候损失函数就是0，换句话说，只要 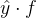 大于1的时候就是完美的了，再大也没有帮助，反映在梯度上就是大于1的梯度均为0，参数不再更新；在0-1之间，它们是同向的，machine 在做分类的时候已经可以得到正确答案，但是 hinge loss 会认为还不够好，他认为要比正确的答案好过一段距离（margin），体现在梯度上就是梯度不为0，还能够通过梯度下降来更新参数使得损失函数继续减小，至于 margin 为啥是1，一个解释是只有1才是 ideal loss 的 tight 的 upper bound 。见上图 紫色 的图例 “hinge_loss”。公式表示如下：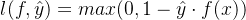

cross entropy VS hinge loss

• 不同点在于对待那些已经能很好的分类的样本，如上图，我们将 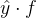 从1挪到2，cross entropy 可以使 loss 下降，所以 cross entropy 会想要好的还要更好，但是 hinge loss 是一个及格就好的损失函数，只要大过 margin 就结束了。
• 相对而言，hinge loss 不是很害怕 outlier ，比较robust

梯度如下图所示：

2.线性SVM

a.function（模型）

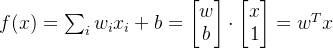
b.损失函数，将每一个样本的损失求和， f 表示给定一个样本 x 模型的输出

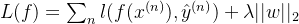
其中

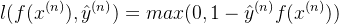
其中后一部分作为正则化的参数向量的2范数使凸函数，前一部分也是凸函数，两个凸函数的叠加仍然是凸函数，尽管不是处处可微的，但是正如引入 relu 激活函数等后基于神经网络的模型依旧可以通过 BP 算法进行参数更新。即使我们很少看到资料上有介绍梯度下降求解 SVM 的，但它确实是可以用梯度下降进行求解的。

此处为了简化，我们暂时不考虑正则化项。

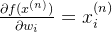
令

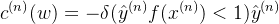
则我们能轻松得到梯度并进行参数更新：

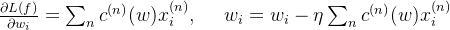
自然了，我们正常见到的 SVM 的损失函数不长这样，下面通过简单的变换来看看我们常见的函数形式。

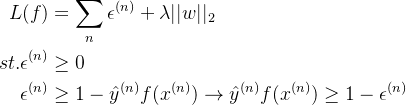
若是去掉约束条件，并令 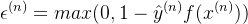 ，但看约束条件和它并不等价，因为它是取两者最大的那一个值，无论何时符合条件的只有一个值；但是约束条件只要符合两个大于等于的条件就可以，有无数的符合条件的值，不过符合约束条件的最小值确是我们新定义的  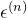的取值。这样我们结合最小化损失函数来看的话，它俩就等价了。

3.kernel

感觉这边讲的 kernel 的方式很新颖。

3.1 前言

参数向量可以看作是样本的线性组合， 

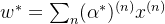
若用0来初始化 w （用0方便理解，非0初始化问题也不大，可以理解为加了偏置），我们再看看之前梯度下降法进行参数更新的式子，若初始值为0，则是所有样本以 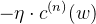 的权重相加，由于采用的是 hinge loss ，所以  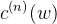通常是0，即不是所有的样本都会被加到 w 里面去，最后解出来的 w 的线性组合的权重可能是 sparse 的，可能有很多样本对应的  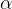值等于0，那些  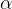值不为0的样本，就是 support vector 。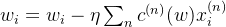

 

我们将 w 由求和写成矩阵向量相乘（分块相乘）的形式，其中矩阵 X 的每一列表示一个样本，我们往常喜欢用矩阵的行表示一个样本，从下式我们更容易看出参数向量可以看作是样本的线性组合：

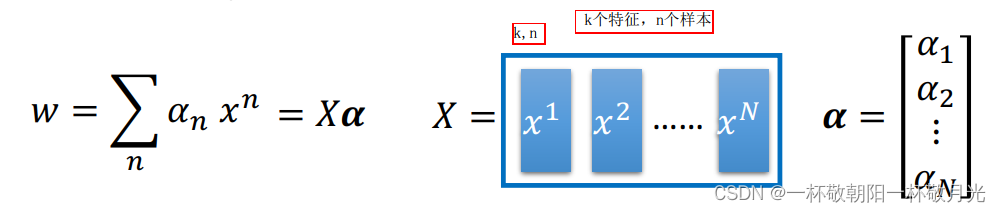
现在有了模型参数，我们就可以在给定一个样本 x（向量）的情况下得到模型的输出结果，输出结果是x和训练集中所有的样本的内积的加权和，其实我们只要知道两个样本的内积就可以拿到输出了，甚至不需要知道这两样本的向量表示，这就是 kernel ：

 

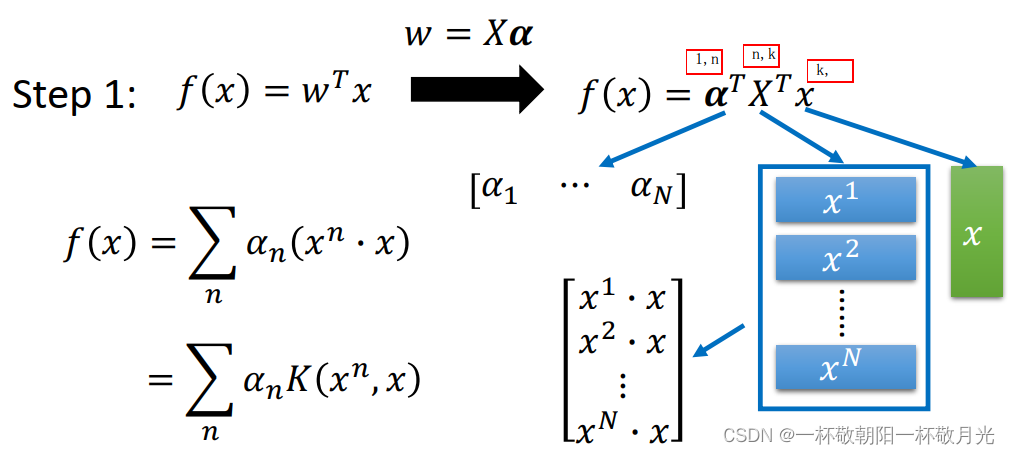
3.2 各种 kernel

其实 kernel 的 trick 不仅仅可以用在 SVM 上，也可以用在其它方法上，例如逻辑回归、线性回归等等。

a.考虑两两的特征交互，可以对原来的 vector 先做内积再平方

把 x 和 z 做 feature transform 再做 inner product ，等价于在原来 feature transform 之前的 space  上面，先做内积再平方。用 kernel 有时候能提升计算效率，上图只考虑了两个特征，若是特征更多的情况下（设有 k 个特征），不使用 kernel 的话，意味着要先对特征考虑两两关系再内积，则新特征有 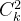 ，做内积也要算  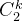的加法，加一次平方；但是用了 kernel ，可以先内积，只需要 k 次运算，然后再做一次平方运算。

b. RBF kernel，无穷维

这种 kernel 会将特征投影到无穷维，容易过拟合，可以通过正则化的手段来缓解。 

kernel 必须能够表示成两个向量的内积，不是所有的函数都能拆成两个向量的内积，但是有一个叫 mercer's 的理论可以告诉我们哪些函数时可以的。 

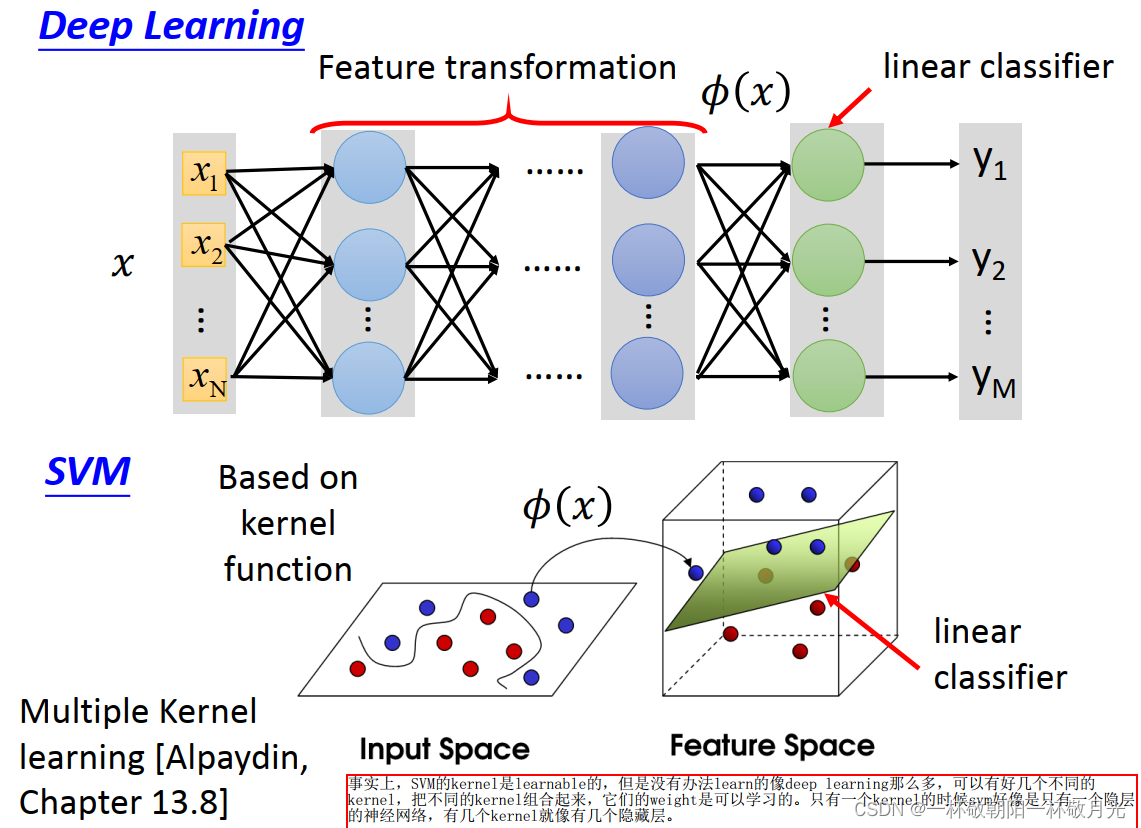
3.3 kernel VS 神经网络

使用一个 kernel 相当于一个隐层的神经网络，隐层的神经元数目就是 support vectors 的数目，每个神经元的权重则对应样本向量，这边做的是 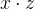，所以还需要过 tanh 激活函数才是 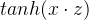， 至于模型的输出则是他们的加权和，所以后续接一个神经元（不带激活函数）做输出。

事实上， SVM 的 kernel 是 learnable 的，但是没有办法 learn 的像 deep learning 那么多，可以有好几个不同的 kernel ，把不同的 kernel 组合起来，它们的 weight 是可以学习的。只有一个 kernel 的时候 SVM 好像是只有一个隐层的神经网络，有几个 kernel 就像有几个隐藏层。

 

 

参考：

https://speech.ee.ntu.edu.tw/~tlkagk/courses/ML_2016/Lecture/SVM%20(v5).pdf

https://www.youtube.com/watch?v=QSEPStBgwRQ