CRF--学习笔记

1. 预知识：
   1. 场（field）：在空间某一区域内，除个别点外，如果对于该区域的每一点p都定义一个确定的量f(p），该区域就称为f(p)的场
   2. 随机过程：设T是一个无限实数集，把依赖于参数t∈T的一族（无限多个）随机变量称为随机过程，记为{X(t),t∈T}
   3. 随机场：若T是n维空间的某个子集，即t是一个n维向量，此处的随机过程又称为随机场。

   4. 马尔可夫随机场（概率无向图模型）：具有马尔可夫性的随机场

   5. 马尔可夫性：P(Y_v | X,Y_w,w≠v) =P(Y_v|X,Y_w,w~v)
      1. w~v：在图G=(V,E)中与顶点v有边连接的所有顶点w
      2. w≠v：除顶点v以外的所有顶点
      3. Y_v，Y_w为顶点v与w对应的随机变量
   6. 团：任意两个顶点在图中相邻。（就是有连线的意思）
   7. 最大团：若C是无向图G的一个团，并且不能再加进任何一个G的顶点使其成为更大的团。
   8. 条件随机场：
      1. 设X和Y是随机变量，P(Y|X)是在给定X的条件下Y的条件概率分布
      2. 若随机变量Y构成一个无向图G=(V,E)表示的马尔可夫随机场，即P(Y_v | X,Y_w,w≠v) =P(Y_v|X,Y_w,w~v)，对任意顶点v成立，则称条件概率分布P(Y|X)为条件随机场。
         1. w~v：在图G=(V,E)中与顶点v有边连接的所有顶点w
         2. w≠v：除顶点v以外的所有顶点
         3. Y_v，Y_w为顶点v与w对应的随机变量
   9.  线性链条件随机场的定义：
      1. 设X=（X_1,X_2,...X_n）,Y=(Y_1,Y_2,...Y_n)均为线性表示的随机变量序列，若在给定随机变量序列X的条件下，随机变量序列Y的条件概率分布P(Y|X)构成条件随机场，即满足马尔可夫性：P(Y_i|X,Y_1,...,Y_(i-1),Y_(i+1),...,Y_n)=P(Y_i|X,Y_(i-1),Y_(i+1))则称P(Y|X)为线性链条件随机场，其中i=1,2,...,n，在i=1和n时只考虑单边。
      2. “线性链条件随机场”又简称为条件随机场（CRF）：

         

         

1. 特征函数定义：

1. 概率无向图的模型的因子分解：

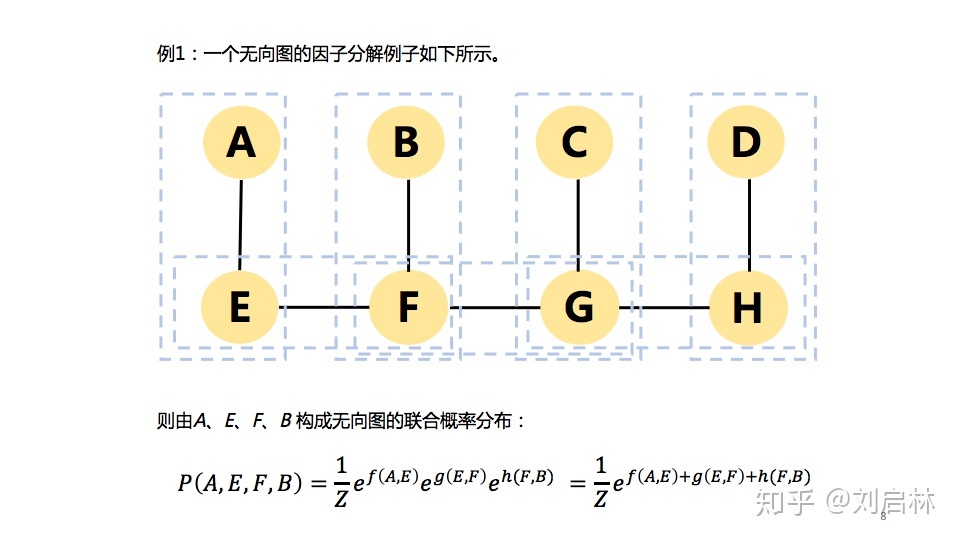
1. 给定概率无向图模型，设其无向图为G，C为G上的最大团，Y_c表示C对应的随机变量。则概率无向图模型的联合概率分布P（Y）可写作图中所有最大团C上的函数φ_c(Y_c)的乘积形式：

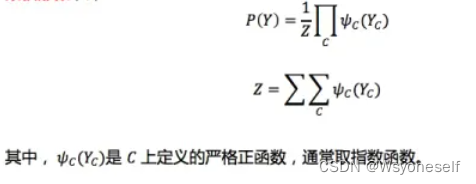
1. 基于CRF由字构词方法的基本思想，基本原理：

 

1. 朴素贝叶斯、HMM、逻辑回归、CRF对比

 

参考：CRF条件随机场的原理、例子、公式推导和应用 - 知乎 (zhihu.com) 

（序号格式一直调不对，大家凑合看吧~）