动态规划--完全背包问题1

代码随想录day44 动态规划模块 完全背包问题
“即使到不了远方，心中也要有远方的模样。”

1.完全背包理论

  有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。完全背包和01背包问题唯一不同的地方就是，每种物品有无限件。

例子：假设背包最大重量为4，然后有三个物品，看如何将物品放入背包中能获取最大价值。

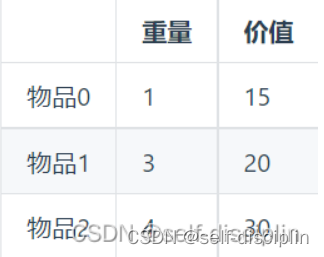
这题跟01背包不同的是，假如还是先遍历物品再遍历背包，01背包在内层for循环的时候是倒序遍历，为的就是不能让物品重复的放入背包，但是呢，现在完全背包问题，刚好能将每个物品多次放入背包，所以顺序遍历即可。

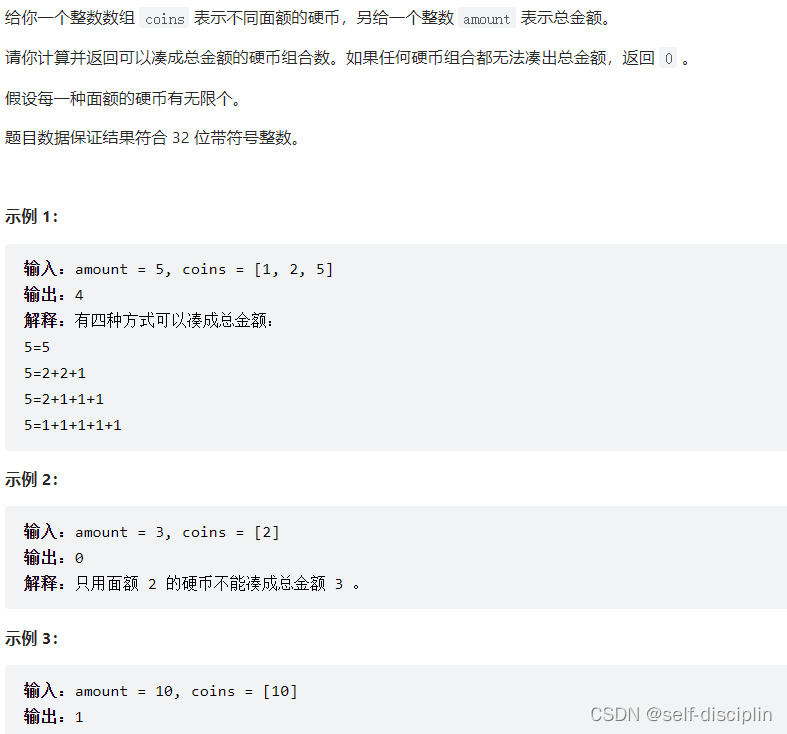
2. leetcode 518.零钱兑换Ⅱ

力扣题目链接

2.1具体步骤及代码实现

  按照动态规划的做题步骤来分析

   1.确定dp数组以及下标的含义

dp[j]表示凑成总金额为j的组合数

   2. 确定递推公式

   假设ament=5

• 当组合中有一个1(nums[i])时候，那么就有dp[4]种方法凑成dp[5]
• 当组合中有一个2(nums[i])时候，那么就有dp[3]种方法凑成dp[5]
• …
• 当组合中有一个5(nums[i])时候，那么就有dp[0]种方法凑成dp[5]

根据下面得出递推公式dp[j]+=dp[j-nums[i]]

  3. dp数组的初始化问题

dp[0]=1

  4.确定遍历顺序

双层都是从前往后的遍历

  5.推导dp数组

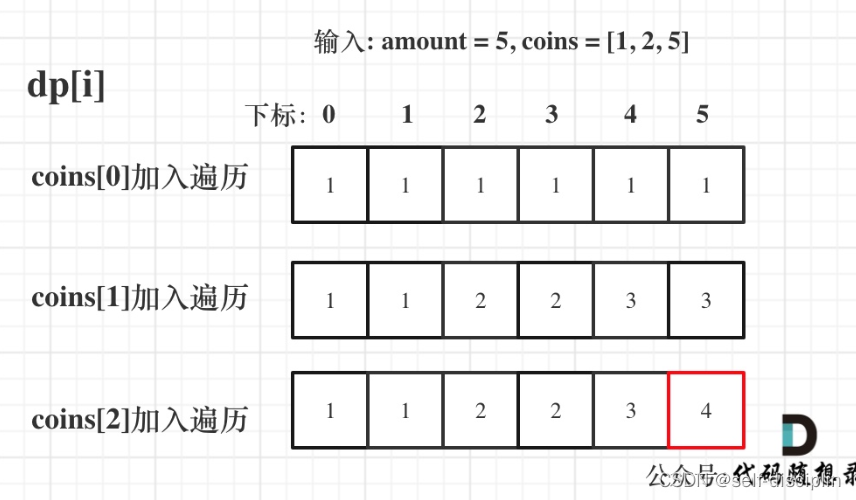
代码实现

class Solution {
    public int change(int amount, int[] coins) {
     int[] dp=new int[amount+1];
     dp[0]=1;
     for(int i=0;i<coins.length;i++){
         for(int j=coins[i];j<=amount;j++){
             dp[j]+=dp[j-coins[i]];
         }
     }   
     return dp[amount];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

---

3.leetcode 377.组合总和Ⅳ

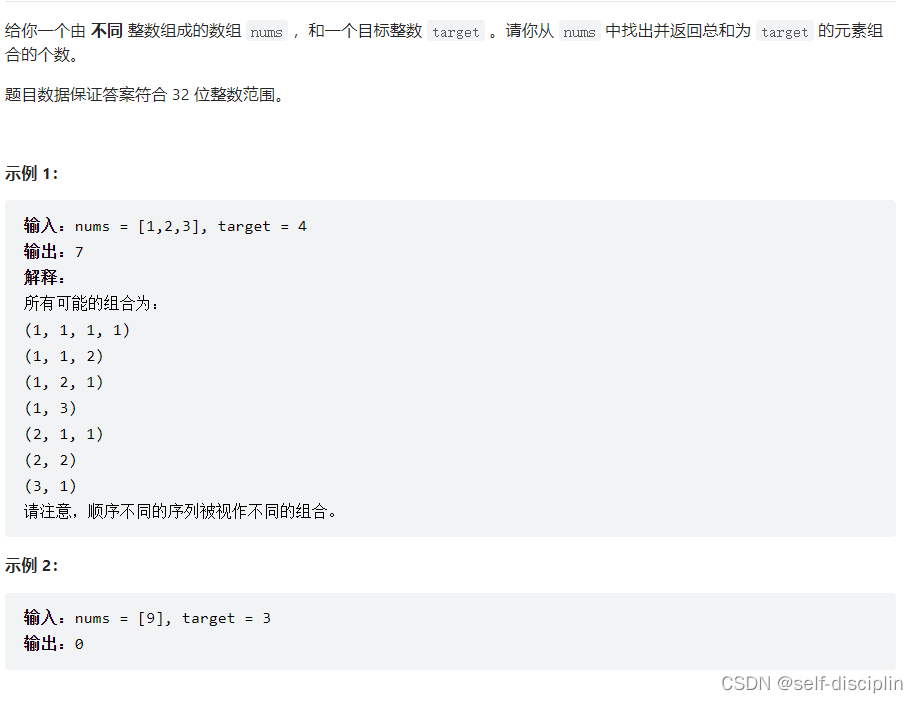
3.1详细思路

这题与上题不同的是还需要考虑排列的方式，也就是得先遍历背包，再遍历物品

3.2具体步骤及代码实现

sp;  1.确定dp数组以及下标的含义

dp[j]表示凑成和为j的排列个数

   2. 确定递推公式

根据下面得出递推公式dp[j]+=dp[j-nums[i]]

  3. dp数组的初始化问题

dp[0]=1

  4.确定遍历顺序

双层都是从前往后的遍历

  5.推导dp数组

代码实现

class Solution {
    public int combinationSum4(int[] nums, int target) {
        int[] dp = new int[target + 1];
        dp[0] = 1;
        for (int i = 0; i <= target; i++) {
            for (int j = 0; j < nums.length; j++) {
                if (i >= nums[j]) {
                    dp[i] += dp[i - nums[j]];
                }
            }
        }
        return dp[target];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14