数据结构学习笔记 6-2 手撕红黑树（上）- 插入调整 与 LeetCode真题（Java）

喜欢该类型文章可以给博主点个关注，博主会持续输出此类型的文章，知识点很全面，再加上LeetCode的真题练习，每一个LeetCode题解我都写了详细注释，比较适合新手入门数据结构与算法，后续也会更新进阶的文章。
课件参考—开课吧《门徒计划》

6-2 手撕红黑树（上）- 插入调整

红黑树也是一种二叉平衡树，我们在上节学习 AVL 树的时候说到，学习一种平衡树，最重要的就是：

• 平衡性质（满足什么样的条件才算平衡）
• 平衡调整策略（如果失衡了 怎样进行调整）

但是我们不是已经学习过一种平衡树 AVL 了吗？为啥还要学红黑树呢？但其实 AVL 是一种高度平衡的二叉树，它的查找效率特别高，每次查找都是 $O(logN)$ 的时间复杂度，但有优点就一定有缺点，它为了维持这种高度平衡的策略要付出很多代价，只要是插入或者删除操作 使得它左右的树高超过 $1$ 了，它就一定会进行旋转调整，当如果面临频繁的插入和操作，而查找操作次数非常少，那么此时就弊大于利了。

此时就引出了新的数据结构——红黑树

红黑树就是普通的二叉搜索树 和 AVL 树的折中，对于平衡策略并没有 AVL 树那么严格。

红黑树的特性是什么？它的适用场景是什么？它能解决什么样的问题？

红黑树的平衡条件

红黑树有以下五大性质：

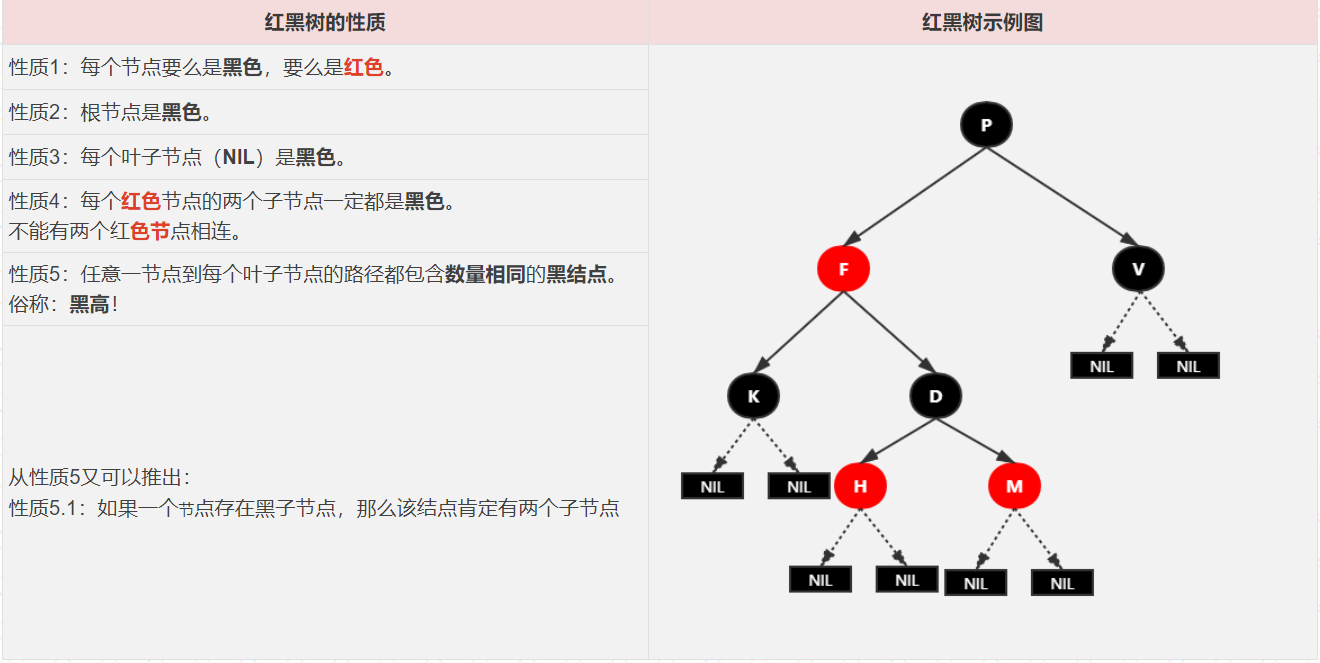
每个叶子节点都是黑色的空节点（NIL节点）。红黑树的叶子节点和我们平时在二叉树上使用的叶子节点的概念是不一样的。

NIL 节点的值没有什么意义，它的作用等同于链表中的 哨兵结点，每一个叶子节点下都会挂两个 NIL 虚拟节点（这里的叶子节点指的是在二叉树中没有子节点的节点，当这个节点只有一个子节点时，也会补上一个 NIL 节点），正常情况下也不会在图中画出来。

NIL 在红黑树的删除操作中会大放异彩，它会起到非常重要的作用，在下一节会讲到。

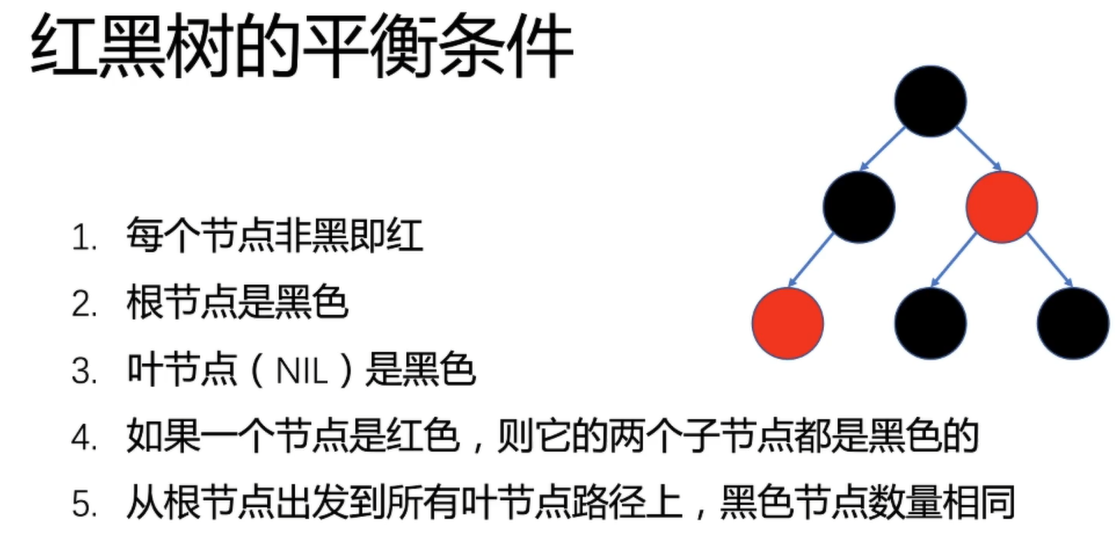
平衡条件引申的问题

第 4 条和第 5 条条件，注定了，红黑树中最长路径是最短路径的长度的 2 倍。

本质上，红黑树也是通过树高来控制平衡的。

红黑树比 AVL 树树高控制条件要更松散，红黑树在发生节点插入和删除以后，发生调整的概率，比 AVL 树要更小。

平衡调整终极法门

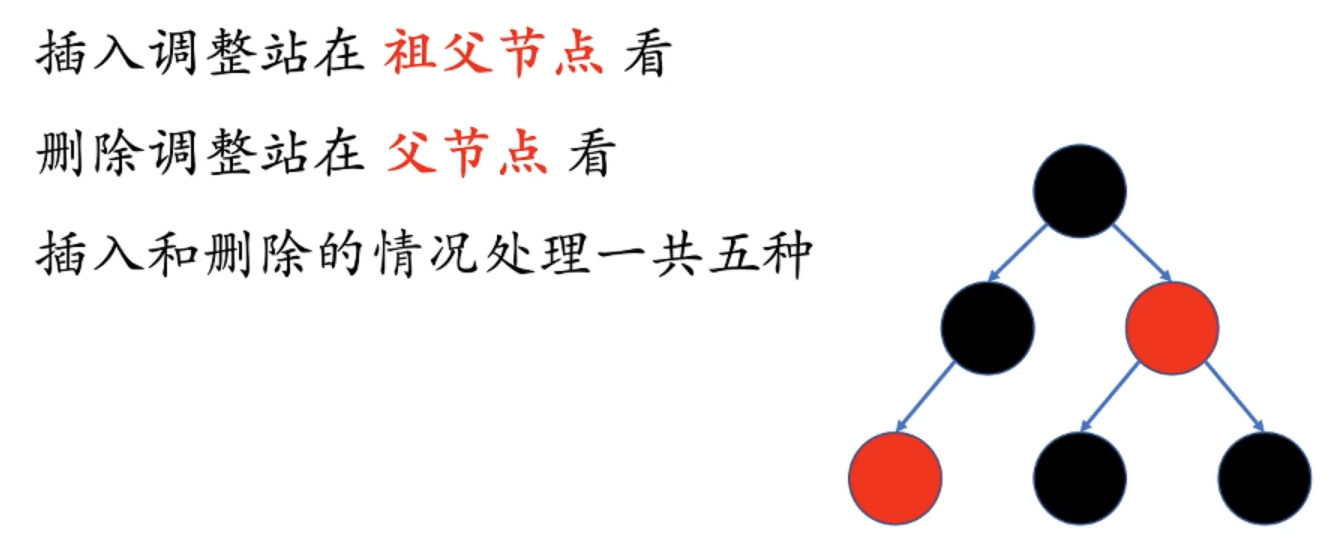
插入调整发生的场景

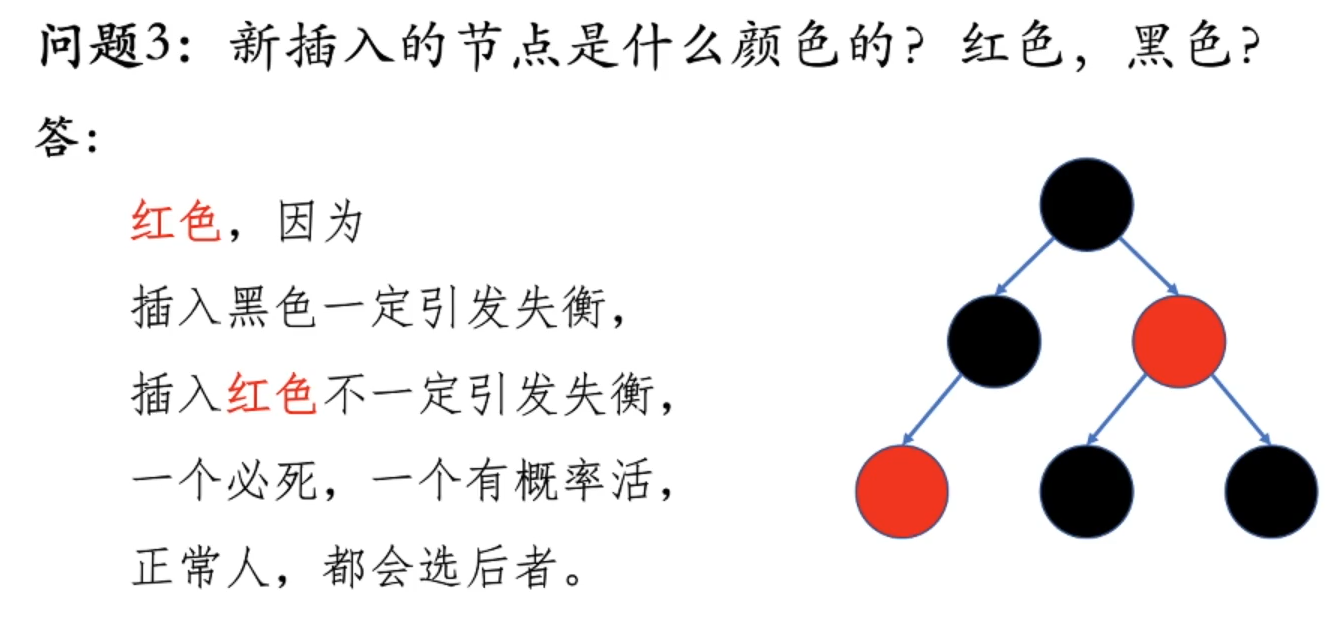
插入调整

插入节点必须为红色。参考性质5，插入红色节点可能会影响平衡，但插入黑色节点则一定会失衡。

情况一

• 叔叔节点为红色的时候，修改三元组小帽子，改成红黑黑。

  

情况二

• 叔叔节点为黑色的时候，参考 AVL 树的失衡情况，分成 $LL,LR,RL,RR$，先参考 AVL 树的旋转调整策略，然后再修改三元组的颜色，有两种调整策略：红色上浮，红色下沉（红黑黑，黑红红）。

• 图中 $LL$ 型失衡就是以 $15$ 节点进行一次右旋，再调整三元组的颜色为 红黑黑 或 黑红红。

  

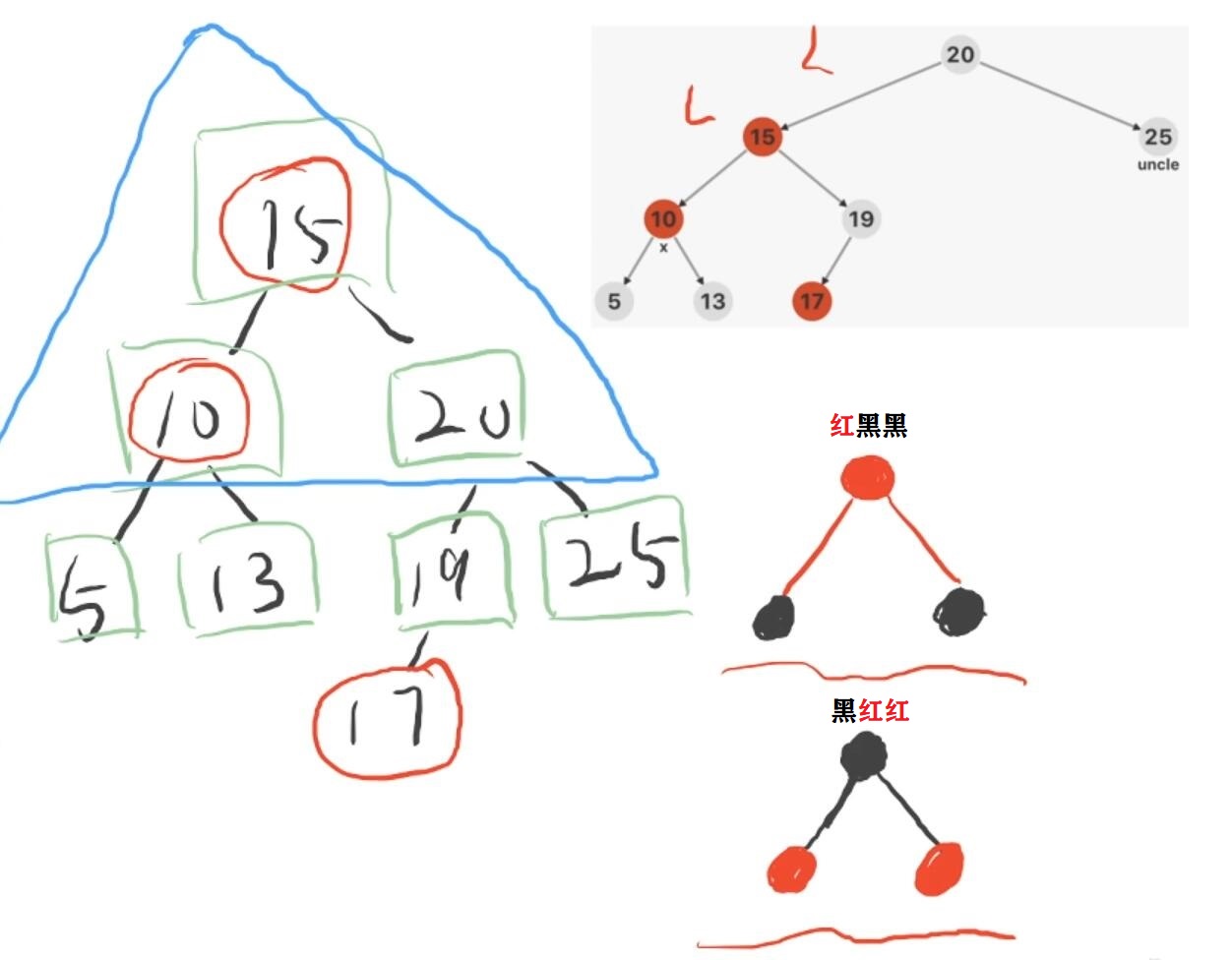
总结

当新插入的节点是红色节点，出现了和父节点冲突的双红情况，我们就看叔叔节点是红色还是黑色：

• 叔叔节点为红色，则为情况一，直接变颜色，不需要旋转。
• 叔叔节点为黑色，则看一下是哪种类型的冲突：$LL,LR,RL,RR$，根据不同的类型进行不同的旋转策略（左旋、右旋），调整完后一定会出现最上方三元组的冲突，我们直接变为 红黑黑 或 黑红红。

我们按照图中的情况只分析了 $LL$ 型失衡，$RR$ 型就是 $LL$ 型的镜像，进行一次左旋即可。

但其实 $LR$ 失衡，就是以 $R$ 进行一次左旋，转换为 $LL$ 失衡，$RL$ 同理。

更详细的插入调整的情况可参考。

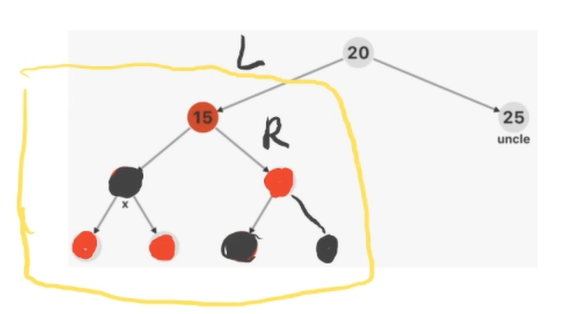
红黑树优势

• 红黑树做的是近似平衡，不是特别的要求高度平衡，所以他的维护成本上，要比 AVL 树低，性价比高。
• 红黑树的插入，删除，查找操作性能比较稳定，很均衡，都是近似 $O(logn)$，适合于我们对性能要求很严格的时候用，比如不能忍受 hash 的 rehash 操作，不能忍受 AVL 树的大量调整的场景，这些场景在工业界中很常见。
• 总结 : 优点是性能均衡，但是没有明显的缺点。

红黑树插入功能代码实现

public class RBTree {

    static Node NIL = new Node();

    // 初始化NIL节点 值为0，颜色为黑色
    private static void init_NIL() {
        NIL.key = 0;
        NIL.color = 1;
        // 把NIL的左子树和右子树都指向自己 这样即使操作NIL的左子树和右子树也不会出现异常
        NIL.lChild = NIL.rChild = NIL;
    }

    // 获取节点 只传入key，默认颜色为红色
    private static Node getNewNode(int key) {
        Node node = new Node();
        node.key = key;
        node.lChild = node.rChild = NIL;
        return node;
    }

    // 插入节点
    private static Node insert(Node root, int key) {
        root = __insert(root, key);
        root.color = 1; // 根节点必须是黑色
        return root;
    }

    // 真正插入节点的方法
    private static Node __insert(Node root, int key) {
        // 如果遍历到NIL节点，则说明可以执行插入操作
        if (root == NIL) return getNewNode(key);
        if (key == root.key) return root;
        if (key < root.key) {
            root.lChild = __insert(root.lChild, key);
        } else {
            root.rChild = __insert(root.rChild, key);
        }
        return insert_maintain(root); // 回溯过程中调整平衡
    }

    // 插入操作调整 => 平衡
    private static Node insert_maintain(Node root) {
        int flag = 0; // 1:R型失衡(RR,RL), 2:L型失衡(LL,LR)
        // 判断当前左儿子是否为红色，且两个孙子是否有红色
        if (root.lChild.color == 0 && has_red_color(root.lChild)) flag = 1; // L型失衡
        // 判断当前右儿子是否为红色，且两个孙子是否有红色
        if (root.rChild.color == 0 && has_red_color(root.rChild)) flag = 2; // R型失衡
        // 未失衡
        if (flag == 0) return root;

        // 此时一定失衡

        // 情况1：红红冲突，叔叔节点为红色
        if (root.lChild.color == 0 && root.rChild.color == 0) {
            // 红黑黑
            root.color = 0;
            root.lChild.color = root.rChild.color = 1;
            return root;
        }
        // 情况2：红红冲突，叔叔节点为黑色 此时为L型或R型失衡 需要左/右旋
        if (flag == 1) { // L型失衡
            if (root.lChild.rChild.color == 0) { // LR
                root.lChild = left_rotate(root.lChild); // 左旋
            }
            // LL 右旋
            root = right_rotate(root);
        } else { // R型失衡
            if (root.rChild.lChild.color == 0) { // RL
                root.rChild = right_rotate(root.rChild); // 右旋
            }
            // RR 左旋
            root = left_rotate(root);
        }
        // 此时只是进行了修改，还未进行染色
        // 染色我们使用“红色上浮” => 红黑黑
        root.color = 0;
        root.lChild.color = root.rChild.color = 1;
        return root;
    }

    // 左旋
    private static Node left_rotate(Node root) {
        Node temp = root.rChild;
        root.rChild = temp.lChild;
        temp.lChild = root;
        return temp;
    }

    // 右旋
    private static Node right_rotate(Node root) {
        Node temp = root.lChild;
        root.lChild = temp.rChild;
        temp.rChild = root;
        return temp;
    }

    // 判断该节点下面是否挂着红色节点
    private static boolean has_red_color(Node root) {
        return root.lChild.color == 0 || root.rChild.color == 0;
    }

    // 前序遍历打印
    private static void output(Node root) {
        if (root == NIL) return;
        // 先输出颜色，再输出值，再输出左子树和右子树的值
        System.out.println("( " + root.color + "|" + root.key + " " + root.lChild.key + " " + root.rChild.key + " )");
        output(root.lChild);
        output(root.rChild);
    }

    public static void main(String[] args) {
        init_NIL();
        Node root = NIL;
        Scanner sc = new Scanner(System.in);
        while (true) {
            int val = sc.nextInt();
            root = insert(root, val);
            System.out.println("=== rbtree print ===");
            output(root); // 前序遍历打印
            System.out.println("=== rbtree print done ===");
        }
    }
}

class Node {

    int key; // 当前节点值
    int color; // 当前红黑树节点的颜色 0:red, 1:black
    Node lChild, rChild; // 左右节点

    public Node() {
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133

输出

94 64 57 21 10
=== rbtree print ===
( 1|94 0 0 )
=== rbtree print done ===
=== rbtree print ===
( 1|94 64 0 )
( 0|64 0 0 )
=== rbtree print done ===
=== rbtree print ===
( 1|64 57 94 )
( 1|57 0 0 )
( 1|94 0 0 )
=== rbtree print done ===
=== rbtree print ===
( 1|64 57 94 )
( 1|57 21 0 )
( 0|21 0 0 )
( 1|94 0 0 )
=== rbtree print done ===
=== rbtree print ===
( 1|64 21 94 )
( 0|21 10 57 )
( 1|10 0 0 )
( 1|57 0 0 )
( 1|94 0 0 )
=== rbtree print done ===
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

我们输入的红黑树就长这个样子：

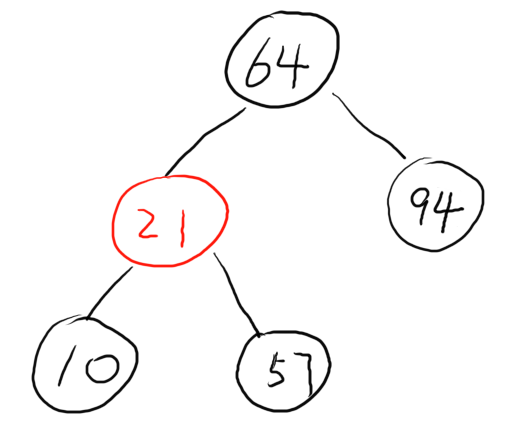
代码很完美！满足了红黑树的五大性质！

---

LeetCode真题

注意：今天的刷题其实没有涉及到红黑树的内容，因为红黑树太偏底层了，很少会有题让你对红黑树中的细节进行更改。

经典面试题—二叉树相关

LeetCode1339. 分裂二叉树的最大乘积

难度：mid

这道题其实可以想到一点：假设有一个数为 $10$，怎么把这个数拆成两个数，使得乘积最大呢？当然是拆成 $5$ 和 $5$，此时乘积最大。

而对于一颗子树拆成两颗子树同理，使分离的两颗子树的节点之和尽可能的相等，如果能一样最好，如果不一样则相差越小越好。

我们可以先DFS一遍求出总和，再DFS一遍深搜出最优解。

LeetCode题解：代码实现

---

LeetCode981. 基于时间的键值存储

难度：mid

这道题就是考察对数据结构的设计。

$1$ 个 $key$ 可以根据时间戳 $timestamp$ 对应多个 $value$。

key  value  timestamp
foo   bar1      1
foo   bar2      2
foo   bar3      3
1
2
3
4

对于 void set(String key, String value, int timestamp) 方法，没什么特别的；

而对于 String get(String key, int timestamp) 方法，假设我们传入的 key, timestamp 为 foo, 4，则按照上方代码块我们返回的值应该是 bar3，timestamp 为 3，因为保证 timestamp_prev <= timestamp，且返回的是最大的 timestamp_prev 中的值。

那么这道题跟树有什么关系呢？

• 这道题做的事情其实就是 插入一些数据，再得到一些数据，并且存储的数据希望它是有序的。
• 重点！！它要找的其实就是该节点的前驱节点！

此时我们就可以利用红黑树的结构来存储，借助语言内置的容器来实现。

而 Java 中我们可以使用 TreeMap，它的底层就是用红黑树来实现的，保证存储的键值对有序。

LeetCode题解：代码实现

---

LeetCode971. 翻转二叉树以匹配先序遍历

难度：mid

给了我们一个预期的二叉树先序遍历结果 $voyage[]$，我们可以翻转任意节点，使它的左右子树交换，最后返回所有翻转的节点。

我们使用先序遍历入手，从根节点开始遍历，先对比根节点是否跟 $voyage[0]$ 相等，如果不相等则直接返回 $-1$，如果相等则往下看第二个节点，如果这个节点跟 $voyage[1]$ 不相等，则对根节点进行一次翻转，再判断是否相等，如果不相等同样返回 $-1$，如果相等 则继续往下递归处理所有节点，重复同样的步骤。

LeetCode题解：代码实现

---

LeetCode117. 填充每个节点的下一个右侧节点指针 II

难度：mid

这道题其实是披着二叉树的链表题。

我们遍历某一层的时候，要把下一层的 $next$ 建出来，但我们遍历的时候 不知道这个节点是否有左右儿子，我们需要自己维护下一层的单向链表；

那么需要用到什么呢？

首先我们每次遍历的时候都需要知道这一层的头结点是谁，需要记录头结点。

我们可以发现每次添加节点的时候，其实是将一个新的点加入到这个链表的末尾节点的后一个节点，也就是让当前链表末尾的 $next$ 指向我们新的节点，所以我们还需要记录尾结点。

• 头结点
• 尾结点

LeetCode题解：代码实现

---

LeetCode剑指 Offer II 053. 二叉搜索树中的中序后继

难度：mid

找出一个二叉搜索树某个节点的中序后继。

而二叉搜索树的中序遍历，就是一个有序的序列，所以这道题我们可以直接中序遍历求得答案。

递归期间，记录当前节点的前一个节点，判断是否为 $p$ 节点。

LeetCode题解：代码实现

---

总结

对于红黑树的学习，最重要的就是红黑树的五大性质，而本文我们讲解了 红黑树-插入调整：

1. 理解红黑树的插入调整，要站在 祖父节点 向下进行调整
2. 插入调整，主要就是为了解决双红情况
3. 新插入的节点一定是红色，插入黑色节点一定会产生冲突，违反条件5，插入红色节点，不一定产生冲突
4. 把每一种情况，想象成一棵大的红黑树中的局部子树
5. 局部调整的时候，为了不影响全局，调整前后的路径上黑色节点数量相同

学习一个新的数据结构就是对比它和其他数据结构的优缺点，具体可阅读上方的红黑树优势。

接下来我们会对于 红黑树-删除调整 进行讲解。