二叉树的最大宽度

题目：

给定一个二叉树，计算二叉树的最大宽度（二叉树的最大宽度是指二叉树所有层次中结点个数的最大值）。

分析：想到求一个二叉树的最大宽度，不难想到层序遍历，即采用入队和出队的方式来寻找二叉树的最大宽度，ok，话不多说，直接开整~

---

• 首先定义一个树的结构体

//树的结构体 
typedef struct BinNode{
	char data;
	struct BinNode *lchild,*rchild;
}BinNode,*BinTree;
typedef BinTree ElemType;//把队列的元素定义为树

lchild和rchild分别代表树的左孩子和右孩子，BinTree为结构体指针；typedef BinTree ElemType；主要是我们需要把树的结点放到队列里面，，所以把队列的元素定义为树~ 

• 利用先序遍历来创建一个二叉树 

void CreateBinTree(BinTree *T)
{
	char ch;
	if((ch=getchar())=='#')	*T=NULL;
	else
	{
		(*T)=(BinTree)malloc(sizeof(BinNode));
		(*T)->data=ch;
		CreateBinTree((BinTree *)&((*T)->lchild));//强制类型转换 (BinTree *)
		CreateBinTree((BinTree *)&((*T)->rchild));
	}
	printf("创建成功！\n");
}

 由于T本身就是指针类型，再传入一个指针即（**T），所以对T进行解引用操作；递归调用函数时（BinTree *）表示强制类型转换。用'#'表示空

 此时树的操作我们已经差不多搞完了，现在要考虑一下什么是树的层次遍历。

由于层次遍历我们需要用到队列，所以我们先写出关于队列的一系列操作~

• 队列的操作

//队
typedef struct Queue{
	ElemType data[MAXSIZE];
	int front,rear;
}Queue,*PtrQueue;
 
//初始化队列
void InitQueue(PtrQueue Q)
{
	Q->front=Q->rear=0;
	memset(Q->data,0,sizeof(ElemType)*MAXSIZE);
}
//判满
int IsFull(PtrQueue Q)
{
    if ((Q->rear+1) % MAXSIZE == Q->front)  return 1;
    return 0;
}
//判空
int IsEmpty(PtrQueue Q)
{
    if (Q->rear == Q->front)    return 1;
    return 0;	
}
//入队
void EnQueue(PtrQueue Q,ElemType *e)
{
	if(!Q || !e)	return;//队为空或者树结点为空
	if(!IsFull(Q)) 
	{ 
		memcpy(&Q->data[Q->rear],e,sizeof(ElemType));
		Q->rear=(Q->rear+1)%MAXSIZE;
	}
}
//出队
void DeQueue(PtrQueue Q,ElemType *e)
{
	if(!Q)	return;
	if(!IsEmpty(Q))
	{
		memcpy(e,&Q->data[Q->front],sizeof(ElemType));
		Q->front=(Q->front+1)%MAXSIZE;
	}
}

队列的顺序存储就不过多介绍了，这里简单介绍一下memcpy函数和memset函数，两个函数都包含在。

 memset（）：C 库函数 void *memset(void *str, int c, size_t n) 复制字符 c（一个无符号字符）到参数 str 所指向的字符串的前 n 个字符。

• str -- 指向要填充的内存块。
• c -- 要被设置的值。该值以 int 形式传递，但是函数在填充内存块时是使用该值的无符号字符形式。
• n -- 要被设置为该值的字符数。

memcpy（）：C 库函数 void *memcpy(void *str1, const void *str2, size_t n) 从存储区 str2 复制 n 个字节到存储区 str1。

• str1 -- 指向用于存储复制内容的目标数组，类型强制转换为 void* 指针。
• str2 -- 指向要复制的数据源，类型强制转换为 void* 指针。
• n -- 要被复制的字节数。

•  层序遍历

 分析：层序遍历即利用队列先进先出的特点，现将根节点入队，若队列不空则将根节点出队，然后将根节点的左右孩子入队再判断队列空不空，若不空则出队一个元素，入队其左右孩子，依次循环~

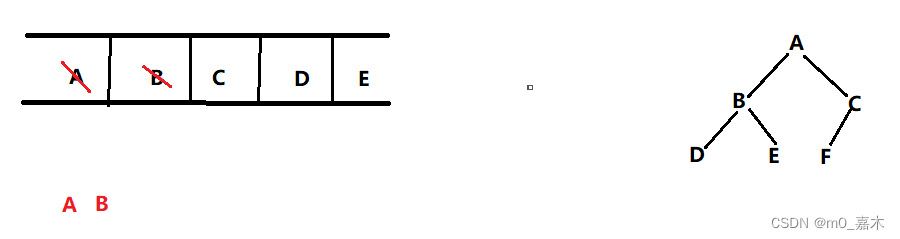
如图所示，左边一颗二叉树，AB表示已经出队，队列里面元素为CDE

//层次遍历
void LevelOrderBinTree(BinTree T)
{
	Queue Q;
	ElemType e=T;
	InitQueue(&Q);
	EnQueue(&Q,&e);
	while(!IsEmpty(&Q))
	{
		DeQueue(&Q,&e);
		visit(e);
		if(e->lchild)	EnQueue(&Q,&e->lchild);
		if(e->rchild)	EnQueue(&Q,&e->rchild);
	}
}

知道了这个原理我们就可以求一个二叉树的最大宽度了~

• 二叉宽度 

//宽度
int WidthBinTree(BinTree T)
{
	if(!T)	return 0;//空树 
	Queue Q;
	ElemType e=T;
	int temp=0,last=0,max=0;//last为一层中最后一个结点在队列的位置， 
	InitQueue(&Q);
	EnQueue(&Q,&e);
	while(Q.front <= last){//每出队一个元素front+1 
        DeQueue(&Q, &e);
        temp++;//temp为树每层的结点个数 
        if (e->lchild != NULL)//每次入队rear+1 
            EnQueue(&Q, &e->lchild);
        if (e->rchild != NULL)
            EnQueue(&Q, &e->rchild);
        if (Q.front > last){//每一层结束后更新 
            last = Q.rear-1;
            max = max > temp ? max : temp;
            temp = 0;
        }
    }
    return max;
}

 按照层序遍历的思路，我们将根节点入队，然后出队，temp表示二叉树每层的结点，每次出队一个元素temp++，然后把根节点的左右孩子入队，判断front指针是否大于last（每层结点最后元素的位置），即判断这一层的元素是否全部出队（全部出队则front与上一次的rear相等，即大于last（rear-1）），如果全部出队则更新last，max（最大宽度）和temp，最后递归所有元素然后返回最大宽度max。

• 完整代码 

#include
#include
#include
 
#define MAXSIZE 100
//树的结构体 
typedef struct BinNode{
	char data;
	struct BinNode *lchild,*rchild;
}BinNode,*BinTree;
typedef BinTree ElemType;
//队
typedef struct Queue{
	ElemType data[MAXSIZE];
	int front,rear;
}Queue,*PtrQueue;
 
//初始化队列
void InitQueue(PtrQueue Q)
{
	Q->front=Q->rear=0;
	memset(Q->data,0,sizeof(ElemType)*MAXSIZE);
}
//判满
int IsFull(PtrQueue Q)
{
    if ((Q->rear+1) % MAXSIZE == Q->front)  return 1;
    return 0;
}
//判空
int IsEmpty(PtrQueue Q)
{
    if (Q->rear == Q->front)    return 1;
    return 0;	
}
//入队
void EnQueue(PtrQueue Q,ElemType *e)
{
	if(!Q || !e)	return;//队为空或者树结点为空
	if(!IsFull(Q)) 
	{ 
		memcpy(&Q->data[Q->rear],e,sizeof(ElemType));
		Q->rear=(Q->rear+1)%MAXSIZE;
	}
}
//出队
void DeQueue(PtrQueue Q,ElemType *e)
{
	if(!Q)	return;
	if(!IsEmpty(Q))
	{
		memcpy(e,&Q->data[Q->front],sizeof(ElemType));
		Q->front=(Q->front+1)%MAXSIZE;
	}
}
//先序创建树
void CreateBinTree(BinTree *T)
{
	char ch;
	if((ch=getchar())=='#')	*T=NULL;
	else
	{
		(*T)=(BinTree)malloc(sizeof(BinNode));
		(*T)->data=ch;
		CreateBinTree((BinTree *)&((*T)->lchild));//强制类型转换 (BinTree *)
		CreateBinTree((BinTree *)&((*T)->rchild));
	}
	printf("创建成功！\n");
}
void visit(BinTree T)
{
	printf("%c",T->data);
}
//层次遍历
void LevelOrderBinTree(BinTree T)
{
	Queue Q;
	ElemType e=T;
	InitQueue(&Q);
	EnQueue(&Q,&e);
	while(!IsEmpty(&Q))
	{
		DeQueue(&Q,&e);
		visit(e);
		if(e->lchild)	EnQueue(&Q,&e->lchild);
		if(e->rchild)	EnQueue(&Q,&e->rchild);
	}
}
//宽度
int WidthBinTree(BinTree T)
{
	if(!T)	return 0;//空树 
	Queue Q;
	ElemType e=T;
	int temp=0,last=0,max=0;//last为一层中最后一个结点在队列的位置， 
	InitQueue(&Q);
	EnQueue(&Q,&e);
	while(Q.front <= last){//每出队一个元素front+1 
        DeQueue(&Q, &e);
        temp++;//temp为树每层的结点个数 
        if (e->lchild != NULL)//每次入队rear+1 
            EnQueue(&Q, &e->lchild);
        if (e->rchild != NULL)
            EnQueue(&Q, &e->rchild);
        if (Q.front > last){//每一层结束后更新 
            last = Q.rear-1;
            max = max > temp ? max : temp;
            temp = 0;
        }
    }
    return max;
}
int main(){
    BinTree T = NULL;
    int width;
    printf("请构造一棵二叉树（#表示空）:\n");
    CreateBinTree(&T);
    printf("层次遍历序列：\n");
    LevelOrderBinTree(T);
    putchar('\n');
	width = WidthBinTree(T);
    printf("树的最大宽度为：%d\n", width);
    return 0;
}