AVL树节点插入方式解析（单旋转和双旋转）

AVL树的规则

在学习AVL树插入节点的方式之前，我们首先要理解为什么要出现AVL树，首先我们要知道的是AVL树是在二叉搜索树的基础上增加一些限制条件才完成的。那么AVL树就是为了处理二叉搜索树的缺点而出现的一棵树，那么普通的二叉搜索树的缺点是什么呢？

假如往树中插入的元素有序或者接近有序，二叉搜索树就会退化成单支树，时间复杂度会退化成O(N)，因此map、set等关联式容器的底层结构是对二叉树进行了平衡处理，即采用平衡树来实现。

而为了解决这个问题，AVL树就在二叉搜索树的基础上增加了这些规则。

它的左右子树都是AVL树

左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)

所以二叉搜索树的全名就是高度平衡二叉搜索树。

上图中的0/1/-1就是平衡因子，平衡因子的定义就是该节点右子树的高度减去该节点左子树的高度。

当然并不是所有的AVL树都是这么实现的，在某些实现方式中，AVL树的实现也是不需要平衡因子的。

那么下面我们就来讲解AVL树的插入。

既然要实现AVL树的插入那么首先要声明和定义的肯定是AVL树节点的声明和AVL树的声明（都是用类完成的）。

首先就是AVL树节点的声明：

template<class K,class T>
struct AvltreeNode
{
	AvltreeNode<K, T>* _left;
	AvltreeNode<K, T>* _right;
	AvltreeNode<K, T>* _parent;
	pair<K,T> _kv;
	int _bt;//平衡因子
	AvltreeNode(const pair<K,T>& t)
		: _left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_kv(t)
		,_bt(0)
	{}
};

这里我使用了类模板和一个pair模板来模拟实现一个keyvalue模式的二叉搜索树。

然后下面我们来声明树

template<class K,class T>
class Avltree
{
public:
	typedef AvltreeNode<K, T> Node;//这里将树的节点重命名，用于下面更加便捷的使用树的节点
 priveat:
   Node* _root;//一棵树自然只会存在一个根节点
};

AVL树的插入

下面我们来解决AVL树的插入问题，首先和二叉搜索树一样，要插入肯定需要先找到插入的位置。

所以第一步还是按照规则使用cur和parent寻找节点。当然是存在一种特殊情况的，那就是如果我们当前的_root = nullptr，那么我们创建好节点，赋值完成后就可以直接return了。

下面我们来写代码。

//下面是寻找插入节点的代码
        if (_root == nullptr)
		{
			_root = new Node(v);
			return true;
		}
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			if (cur->_kv.first > v.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_kv.first < v.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;//这里是key相等的情况，avl树依旧是不允许重复key的差入这里直接返回false即可
			}
		}//当运行到这里的时候，代表的就是找到了需要插入的位置。

在找到插入位置之后，下面只需要创建出节点然后将其连接到父节点上即可。

这里需要注意的是我们在将创建好的节点连接到父节点上时，还需要注意一个点那就是不要忘了我们这里节点的结构时三叉链形式的，所以在修改完后不要忘记了要将先创建节点的parent指针修改指向。

下面是代码：

        cur = new Node(v);//给cur创建空间，这一步用于下面的计算平衡因子
		if (parent->_kv.first < v.first)
		{
			parent->_right = cur;
			cur->_parent = parent;//完成三叉链的连接。
		}
		else
		{
			parent->_left = cur;
			cur->_parent = parent;
		}

以上其实和二叉搜索树是一样的，而二叉搜索树的插入到这里就结束了，但是AVL树的插入到这里其实才算是开始，因为下面我们要管控平衡因子，来做到让AVL树做到尽可能的平衡。

因为在插入了新节点之后，我们需要去更新平衡因子，新节点的插入可能会引起到达这个节点路径上的平衡因子发生变化。

这里根据平衡因子的定义，我们可以知道如果是在父节点的右子树上插入新节点，那么父节点的平衡因子会+1,如果是在左子树上插入那么父节点的平衡因子会-1。

​因为在极端情况，例如左右高度差相差很大的时候，普通的搜索二叉树的搜索时间复杂度就很高了。

下面是AVL树的特点。

平衡因子等于右子树的高度减去左子树的高度。

那么这里有第一个问题，为什么这里的左右高度差不是相等，而是不相差于1？

因为做不到。总会存在一些情况高度差不相等，例如只有两个节点或者是4个节点的情况

而左右高度差是1，还是可以做到的。

而我们在实现的时候，可以使用一个平衡因子来帮助我们判断，（这个平衡因子不是必须的，有些地方实现也没有使用平衡因子）。

此时AVL树查找的效率基本就能够控制在logN了。基本上缺节点也是在最后两层。和完全二叉树是很相似的，所以查找的时间复杂度就是logN

平衡因子的更新

这里使用下面的这颗树作为例子来解释插入后的操作

第一个如果我在下面这里插入了一个cur，第一步肯定是需要去更新平衡因子

此时的父节点应该--。

这里存在一个结论：插入节点可能会影响祖先，但是不会影响旁支。例如上面的这个节点在影响了c的父节点之后，就不会继续往上更新了，原因也很简单，因为在插入了c之后，8的高度变成了0，也就是8的高度没有变化，之前8的高度是1，也就是右边高左边矮，而在往左边插入节点后，两边的高度一样了，但是在7计算高度的时候，一直都是按照8的最高高度来计算的。所以这里c的插入只会影响8，不会在往上影响。

总结：

例如下图：

此时9的高度变化了，所以8的平衡因子也就变成2了，8的高度变了自然也会影响7，但是在继续往上更新前，

这里的这颗树已经出问题了，所以这里需要处理一下。

总结一下规则：

如果我在插入之前父节点的bf = 2/-2，代表在插入前这个二叉树已经不是AVL树了已经需要单独处理了。这里的调整也就是对节点进行旋转，也是重点内容。

那么存不存在这三种情况都停不住的状态呢？答案是肯定的例如下图：

此时已经更新到根节点了，如果不停止还会继续往上更新，所以这里我们还需要设置一个循环停止条件，因为如果此时还在往上更新会出现空指针的解引用。所以在下面的代码中我们就将while循环中填入了parent，就是为了防止在遇到根节点之后还在往上面更新。

下面是整体的代码：

while (parent)//防止出现更新到根节点了还在往上更新。
		{
			if (parent->_left == cur)
			{
				parent->_bt--;//更新平衡因子，因为cur插入在了parent的左边，所以这里是让parent的平衡因子--
			}
			else
			{
				parent->_bt++;//插入在右节点是让parent的平衡因子++
			}
			if (parent->_bt == 0)
			{
				//这是最好的一种情况在节点插入之后，parent的高度恰好是插入在1了低的那一端此时的整棵树都是平衡的可以直接结束插入
				break;
			}
			else if (parent->_bt == 1 || parent->_bt == -1)
			{
				//这里代表的是parent的高度已经改变了需要继续往上处理，这里可以使用递归但是，能够使用循环
				//还是尽量使用循环比较好
				cur = parent;//让cur等于parent
				parent = parent->_parent;//让parent继续往上
			}
			else if (parent->_bt == 2 || parent->_bt == -2)//此时已经存在了平衡问题需要旋转处理了
			{
				//这里就是需要旋转的情况
			}
			else
			{
				//出现了其它的问题，即在旋转之前已经不是一个AVL树了
				assert(false);
			}
		}
		return true;//在插入完成之后返回true
	}

左单旋

这里先给出一个结论：右边高，那就使用左单旋

下面我们来看旋转：

例如这里当你插入3的时候就会出现问题了（不平衡）。

首先旋转的目的是让左右均衡  所以这里存在的问题是右边高（1高度为2，所以需要往左边旋转），在旋转的时候，还需要保证一个东西那就是，要让旋转后的树也要保持搜索树的规则。否则在旋转后不是搜索树了，那还有什么旋转的必要。

下面我们来学习如何左旋。

将2压下来。

下面我们来看一个左旋更为复杂的情况。

此时怎么搞呢？此时这两张图都是右边高

首先9必须下来，不能在让19作根节点了。

然后下面是左单旋的抽象图：

为何使用抽象图呢？因为实际情况很多很多。所以这里就使用抽象图了，我们只需要记住，虽然实际的情况非常的多，但是只需要使用抽象图，那么就能够使用一个唯一的方法去解决这些情况

a/b/c是高度为h的AVL子树。

这里我们分别来分析一下h为0，h为1，和h为2时的abc的状态。

红圈为插入节点

此时都会引发旋转，但是旋转的方式都是不变的。

让60的左边b成为30的右边，然后让整个30成为60的左边。此时的抽象图就是对实际情况的归类，但是实际情况是存在无数种的，因为h可以等于0，1，2，3，4，5，6.当h等于2的时候，AVL树都存在三种，以下的三种都是可以放到abc，那三个位置的。

那么当h等于2的时候有多少种情况呢？

首先c为什么一定是x呢？因为c这个位置需要插入节点，然后引发旋转，但是如果c的选择是x或者是y，那么如果c为z/y刚好这样插入呢？

如果是插入在了y的左边和z的右边就不会出现旋转，所以c只能是x。

那么如果这里我们进行一个排列组合：

a和b都是3选一那就是3*3,而在c的插入位置存在4个，所以这里的可能情况有3*3*4 = 36种。

这还只是h为3，所以这里选择画抽象图，而不是具象图。但是无论下面的情况，我们旋转的还是那几个节点（30，60,c）。

我们只需要记住左旋旋转的逻辑即可。

这里旋转的细节就是下面：

此时完全的遵循了搜索树的规则。

这里subRL可能为空，当abc高度为0的时候subrl就为null

然后是平衡因子的修改abc不需要修改平衡因子，只需要修改parent和subr的平衡因子，因为ac没有动过b虽然动了，但是并没有动b的子树（平衡因子的定义就决定了，平衡因子的改变只会和子树有关），所以这里需要这么写。然后下面是和这个一样类似的右单旋（自然是左边高了）

下面是左单旋的代码：

//下面我来实现一个简单的左单旋(右边高)
//这里为了便于理解你可以将parent看作是抽象图中的30，subr则是60，sublr则是b子树的根节点（注意这里的b可能为空）
	void RotateL(Node* parent)//这里我们将节点平衡因子为2的节点设置为一个parent
	{
		Node* parent_parent = parent->_parent;
		Node* SubR = parent->_right; // 代表平衡因子为2节点的右节点
		Node* SubRL = SubR->_left;//同理上一个节点的左节点
		//记住左单旋的图
		parent->_right = SubRL;//让subr的左节点给parent的右节点
		//但是这里sunrl可能会空所以需要判断一下
		if (SubRL) {
			SubRL->_parent = parent;//此时的subrl的父节点已经改变了
		}
		SubR->_left = parent;//让subr的左节点指向parent
		parent->_parent = SubR;
		//但是在这里不要忘记了，我们的节点是一个三叉链的结构
		//所以下面我们还需要去修改parent的指针，否则依旧会出错
		//这里最后还需要单独的处理一下一种特殊的情况那就是
		//parent刚好就是根节点
		if (_root == parent)
		{
			_root = SubR;//需要更新一下根节点
			SubR->_parent = nullptr;//此时的subr是根节点，根节点自然不再存在父亲节点了
		}
		else//此时的根节点不是parent
		{
			if (parent_parent->_left == parent)
			{
				parent_parent->_left = SubR;
			}
			else
			{
				parent_parent->_right = SubR;
			}
			//让paren_parent原先指向parent的指针重新指向subr
			SubR->_parent = parent_parent;
		}//经过这一步如果这里的parent是一个局部的子树，我就能将这颗子树和上面的节点连接起来
		//最后我们需要修改一下这颗树的平衡因子。
		//根据抽象图，abc的平衡因子是不需要改变的，选哟改变平衡因子的是parent和subr的平衡因子
		parent->_bt = 0;
		SubR->_bt = 0;//修改平衡因子。
	}

最后修改平衡因子，也是根据抽象图平衡后算出来的。

右单旋

结论：左边高则使用右单旋

抽象图：

上图就是右单旋转的抽象图，小细节基本和左单旋一样。

细节就是将30的右子树变成60的左子树，然后让30成为60的父节点。

这里假设一棵树在完成插入和旋转之后，还需不需要在继续往上更新平衡因子呢？

答案是不需要因为我们要理解旋转的本质：

例如在上面的插入节点后根节点（60）的左子树高度为h+2,但是旋转之后根节点（30）的左节点就变成了h+1，明显降低了高度。

下面是右旋的代码：

//下面我们来完成右单旋（左边高）
	void RotateR(Node* parent) 
	{
		Node* SubL = parent->_left;//依旧是找到那三个节点
		Node* SubLr = SubL->_right;
		parent->_left = SubLr;
		if (SubLr) {
			SubLr->_parent = parent;//完成对parent左节点的重新赋值
		}
		SubL->_right = parent;
		Node* parent_parent = parent->_parent;//依旧是用于将此时我们旋转后的局部AVL树连接到整体树上
		parent->_parent = SubL;
		if (_root == parent)
		{
			_root = SubL;//这里依旧是parent是根节点的一种情况
			SubL->_parent = nullptr;//祖先节点无父亲。
		}
		else
		{
			if (parent_parent->_left == parent)
			{
				parent_parent->_left = SubL;
			}
			else
			{
				parent_parent->_right = SubL;
			}
			SubL->_parent = parent_parent;
		}
		//最后是修改平衡因子
		parent->_bt = 0;
		SubL->_bt = 0;
	}//由此就完成了AVL树右单旋的处理。

下面是双旋转：

右左双旋

结论：这里其实是先右边高然后变成了左边高。

我们分治的处理，先使用一个右旋让其全部变成右边高，然后使用一个左旋解决问题。

此时我在b插入一个新节点。此时如果你还是进行一个左单旋转

此时高度也没有降低，也没有平衡。所以这里只使用一个左单旋转是无法解决问题的。因为这里不是一个单纯的右边高，这里是右边高然后是左边高。

所以想要处理这里的情况我们需要使用双旋转。先使用抽象图：

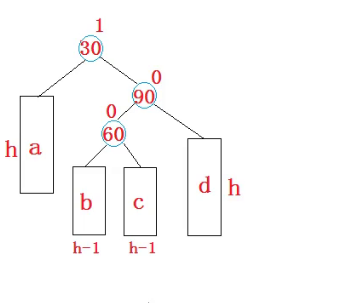
这里我对b又进行了一次拆解将其拆解成了两棵树。

首先在什么位置插入会引发问题呢？首先a和d是高度为h的AVL树，b和c是高度为h-1的AVL树。b和c可能是空树

那么我们的新增可以新增加在那里呢？b和c后面都可以进行新增，或者如果b和c是空树，那么60就是新增。需要使用双旋转解决问题。

下面是常见的场景：

此时就需要使用双旋转。

这里是高度为2的场景。

下面我们粗略分析一下高度为三的情况：

可以看到累计场景的数量是非常的恐怖的，这还只是高度为3的情况，后面的高度数量只会呈现几何倍数增长。

但是无论你的场景有多少，对于双旋转的场景依旧是和左/右单旋转一样。

我们通过抽象图来理解：

第一种b新增：

第二种c新增：

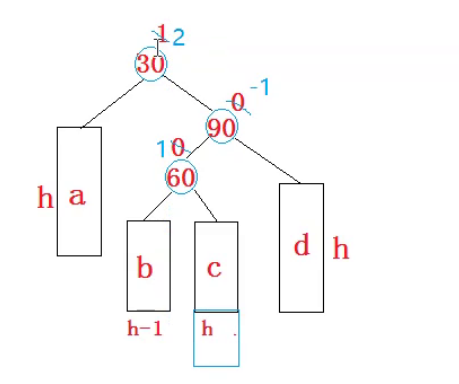
这里要用双旋转来解决是因为不纯粹了（不是单纯的左高和右高），所以需要双旋转了

第三种60自己就是新增

上面两种我们可以归类为h是大于等于1的AVL树，最下面这一种是h为0的AVL树。我们分开是因为虽然旋转的过程是一样的，到那时需要按照不同的情况，去处理不同的平衡因子。

那么首先双旋转的大思路都是：

这里的妙处就在于右单旋，将这一棵不纯粹的树变成了右边高的树。最后使用一个左旋转完成结束

,那么这种情况旋转完成后的平衡因子如何更新呢？

首先abcd平衡因子不动（b之前已经更新过了）30，60，90的孩子都动了所以需要修改平衡因子

然后我们要根据抽象图中60的平衡因子的不同（旋转前），来判断最后平衡因子的更新。

下面是60的平衡因子为-1

此时根据最后的平衡图我们能够知道parent(30)，subRL（60）平衡因子为0，subR（90）的平衡因子为1

下面如果是在c插入，此时的60平衡因为为1

此时根据最后的平衡图我们能够知道subR，subRL（60）平衡因子为0，parent(30)的平衡因子为-1

最后如果60就是插入的节点

这种情况下无论是哪一个节点最后的平衡因子都是0.

以上都是右左双旋的场景，但是这三种情况最后双旋出的平衡因子也是不同的。

下面是代码的实现：

void RotateRL(Node* parent)//右左双旋转
	{
		Node* SubR = parent->_right;
		Node* SubrL = SubR->_left;
		int count = SubrL->_bt;//首先取得此时的平衡因子，不然经过后面的旋转平衡因子可能会被改变
		RotateR(SubR);//首先以parent的右节点为轴进行一个右旋转
		RotateL(parent);//再以parent为轴进行一个左旋转。
		//然后我们要根据不同的情况对平衡因子进行判断
		//即要将三种情况分析出来，不然无法完成平衡因子的区分，这里可以使用抽象图中60所在的那个位置的平衡因子能够帮助我们区分这三种情况
		if (count == 0)
		{
			//代表的就是60自己插入的情况
			parent->_bt = SubR->_bt = SubrL->_bt = 0;
		}
		else if (count == 1)// 代表的是在抽象图中的c位置后面插入的情况
		{
			SubR->_bt = SubrL->_bt = 0;
			parent->_bt = -1;
		}
		else if (count == -1)//代表的是在抽象图的b位置后面插入节点的情况
		{
			SubR->_bt = 1;
			SubrL->_bt = parent->_bt = 0;
		}
		else
		{
			assert(false);//出现了错误的情况，不需要在进行平衡了
		}
	}//由此就完成了

左右双旋

结论：这里的结构就是首先左边高，然后是右边高。为了处理右边高我们首先使用一个左旋（30为轴），将整个树变成整体都是左边高的情况，然后再使用一个右旋转。

下面我们来看左右双旋的情况

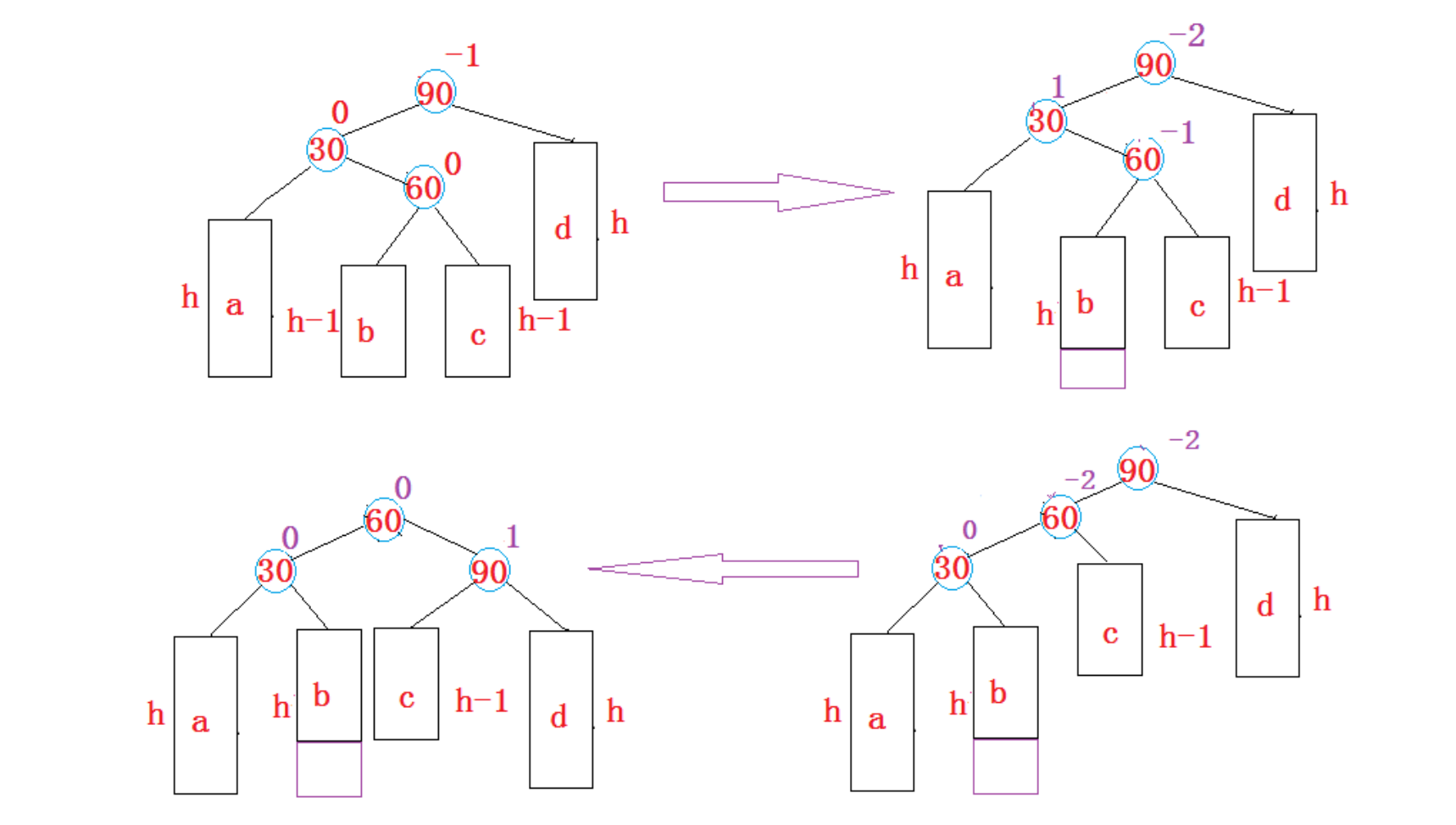
以上抽象图依旧是按照60节点所在的平衡因子的情况可以分成三种情况（-1,0,1）

上面抽象图最后显示的是为-1的情况

即在b处插入节点后60平衡因子变成了-1的情况。（在b插入）

可以看到最后平衡后的平衡因子subLR（60）为0，而parent（90）为1，subL（30）为0.

如果60自己就是新增节点的情况。

可以看到最后平衡后的平衡因子subLR（60）为0，而parent（90）为0，subL（30）为0.

在b处插入节点后60平衡因子变成了1的情况。在c处插入。

可以看到最后平衡后的平衡因子subLR（60）为0，而parent（90）为-1，subL（30）为0.

然后下面是代码：

void RotateLR(Node* parent)//左右双旋
	{
		Node* subL = parent->_left;
		Node* sublR = subL->_right;
		int count = sublR->_bt;//依旧是以这个情况为准来进行平衡因子的判断
		RotateL(subL);//首先以subl为轴进行一个左旋转
		RotateR(parent);//再以parent为轴进行一个右旋转
		if (count == 0)
		{
			parent->_bt = subL->_bt = sublR->_bt = 0;
		}
		else if (count == 1)//再抽象图的c位置后面插入
		{
			parent->_bt = sublR->_bt = 0;
			subL->_bt=-1;
		}
		else if (count == -1)
		{
			parent->_bt = 1;
			subL->_bt = sublR->_bt = 0;
		}
		else
		{
			assert(false);
		}
	}

在我们完成了插入节点后可以使用一些代码去验证，第一种方式，插入数据后使用中序遍历打印一下。

但是这样打印出来一个升序的结果，只能证明这是一个搜索树，不能证明这一个AVL树，所以我们还需要些一个验证平衡的代码，即求出每一个节点的左右高度差（右子树高度减去左子树高度），如果不等于平衡因子，则证明我们的AVL树出现了错误。

bool isblance()
{
		return _isblance(_root);
}
 bool _isblance(Node* root)
{
		if (root == nullptr)
		{
			return true;
		}
		int lefthigh = Hight(root->_left);
		int righthigh = Hight(root->_right);
		if (righthigh - lefthigh != root->_bt)
		{
			cout << root->_kv.first << "当前节点平衡因子异常" << endl;
			return false;
		}
		return abs(righthigh - lefthigh) < 2&&_isblance(root->_left)&&_isblance(root->_right);
}

最后你还可以使用一个随机数代码，将一些随机数插入到树中。

下面是我的验证代码：

希望这篇博客能对你有所帮助，写的不好请见谅。如果发现了任何的错误，欢迎指出。