LeetCode 43. 字符串相乘

---

1. 题目描述

题目链接：43. 字符串相乘

2. 解题思路

这道题在力扣上有很多题解，但是我觉得看着都不咋个明白，所以重新梳理了过程。

我这里只讲解比较优的一种方法。

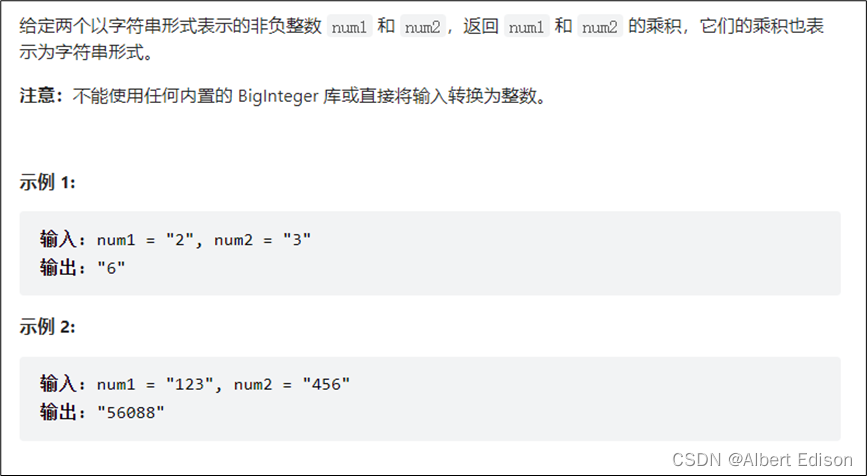
假设 num1 = 1234，num2 = 567，则把 num1 的每一个数乘以 num2 的每一个数的结果直接写出来（不用考虑进位）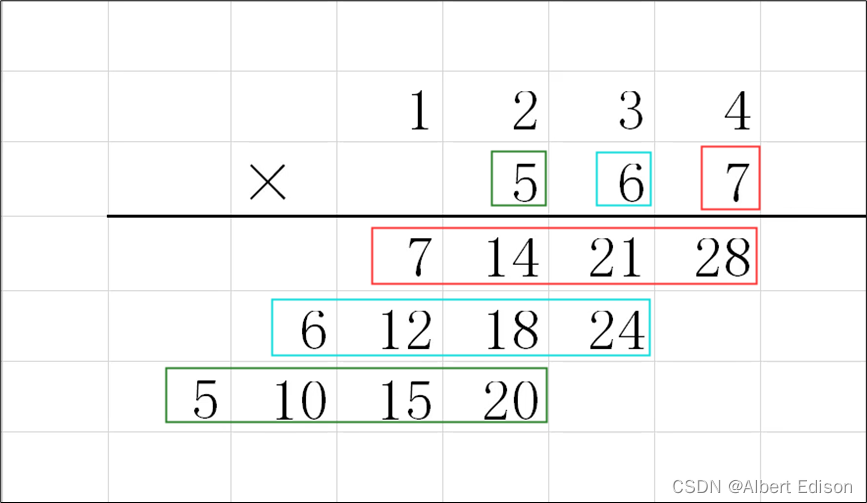

因为我们只是进行了单纯的数学运算，没有涉及任何字符串有关的操作，所以我们可以建立一个数组 ansArr 用来保存每一列相加的总和。

那么这个 ansArr 应该开多大空间呢？

很简单，两个数相乘的乘积最长是两个数长度之和，比如 $999\ast 999=998001$

而两个数相乘的乘积最短是两个数长度之和再减1，比如 $100\ast 100=10000$

我们默认开最长的空间。

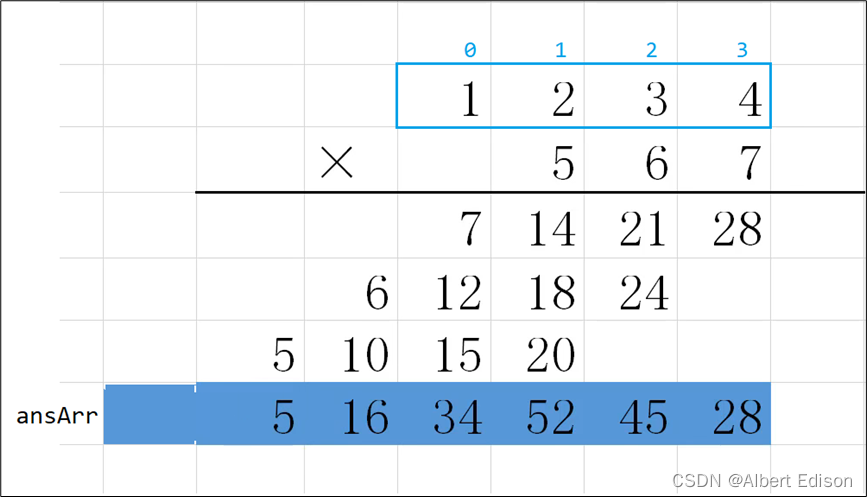
我们建立数组的目的是想把每一列的数都存起来，那么在实现代码的时候，应该怎么写才能把每列的数放到数组中正确的位置呢？

很简单，我们把 num1 的某一位称为第 i 位，把 num2 的某一位称为第 j 位，它们相乘的结果应该是位于数组的 i+j+1 的位置：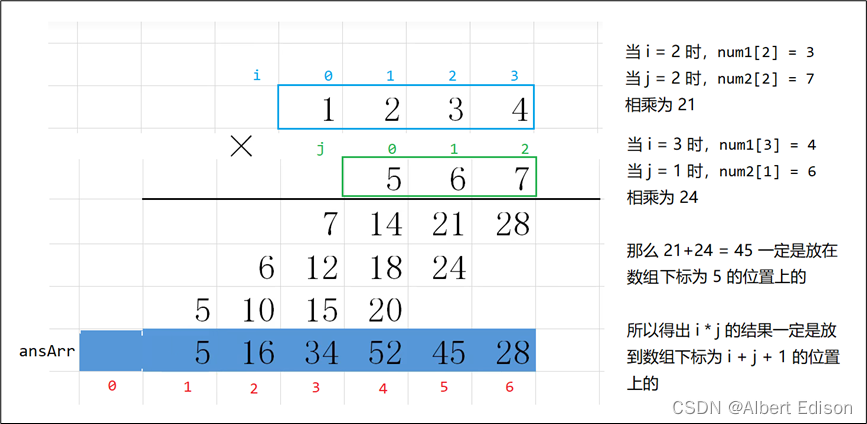

然后我们只需要从 ansArr 数组的最后一个位置开始，往前遍历，依次进位。

比如 ansArr[5] = ansArr[5] + ansArr[6] / 10，然后 ansArr[6] %= 10，此时 ansArr[6] = 8，然后向前进 2 位，所以 ansArr[5] = 47

最后再定义一个字符串 ans，把 ansArr 的数字存进去就好了（记得要把数字转换成字符）。

这里还有一个特殊情况，比如上面的 ansArr 数组开了 7 个空间，但是第一个位置是没有值的，所以我们往 ans 里面插入数据的时候，要判断一下，假设第一个位置是 0 的话，那么就从第二个位置开始插入数据。

int index = ansArr[0] == 0 ? 1 : 0;
1

这种方法是比较优的一种，时间复杂度分析为 $O(n\ast m)$，n 和 m 分别是 num1 和 num2 的长度。

3. 代码实现

代码示例

class Solution {
public:
    string multiply(string num1, string num2) {
        if (num1 == "0" || num2 == "0") {
            return "0";
        }
        int len1 = num1.size();
        int len2 = num2.size();

        //两个数相乘的乘积最长是两个数长度之和，比如 999 * 999 = 998001
        //两个数相乘的乘积最短是两个数长度之和再减1，比如 100 * 100 = 10000
        //默认开最长
        vector<int> ansArr(len1 + len2);

        for (int i = len1 - 1; i >= 0; i--) {
            int x = num1[i] - '0'; //把num1的字符转换为数字
            for (int j = len2 - 1; j >= 0; j--) {
                int y = num2[j] - '0'; //把num2的字符转换为数字
                ansArr[i + j + 1] += x * y;
            }
        }

        //进位
        for (int i = len1 + len2 - 1; i > 0; i--) {
            ansArr[i - 1] += ansArr[i] / 10; //前一位=后一位的进位值+自己
            ansArr[i] %= 10;
        }

        //拼接（判断前导0的情况）
        //[0] [] [] []
        string ans;
        int index = ansArr[0] == 0 ? 1 : 0;
        while (index < len1 + len2) {
            ans += (ansArr[index] + '0');
            index++;
        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39