-
【算法篇-字符串匹配算法】BF算法和KMP算法
前言
本文章是基于比特大博哥在B站讲解 KMP 算法的一篇总结，
视频链接：
KMP讲解字符串匹配问题： 字符串匹配问题，就是在一个长字符串S中，选择一个子字符串D的位置 比如字符串 char S[] = "ecfabctgabcdlghe"; 字符串 char D[] = "abcd"; 如何才能高效地在S中寻找到包含字符串D起始的位置？ 对此，产生了各种各样的算法。 下面，主要介绍BF和KMP算法。- 1
- 2
- 3
- 4
- 5
- 6
- 7
1. BF算法
BF算法，即暴力(Brute Force)算法。- 1
一种比较低效的算法，但是思路很简单。 大致就是先从字符串S的第一位与字符串D的第一位做比较， 如果两个第一位都相等，则继续比下去， 比较字符串S的第二位和字符串D的第二位 直到字符串D走完为止。 字符串D如果能顺利走完，则说明字符串S的第一位就是我要找的起始位置。 如果比较的过程中不相等，则字符串S要从第二位开始与字符串D的第一位继续比较。 一直进行下去，直到找到。 如果字符串S走完了，说明字符串S中不包含字符串D 如果字符串D走完了，说明字符串S中包含了字符串D，返回S刚开始比较的位置。 文字描述很难理解，我们画个图就明白了。- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
1.1 画图分析
首先，拿字符串S的第0位开始与字符串D的第0位比较，
因为两者一开始就不一样，所以字符串S要从下一位开始与字符串D比较。
此时 i++
字符串S中 i 指向的字符仍然和J指向的字符不一样
i继续往后走
i++
仍然不一样
i继续往后走
i++
此时，i 和 j 指向的字符一样了，
那么字符串D 的 j 可以同时和 i 继续往后比对了。
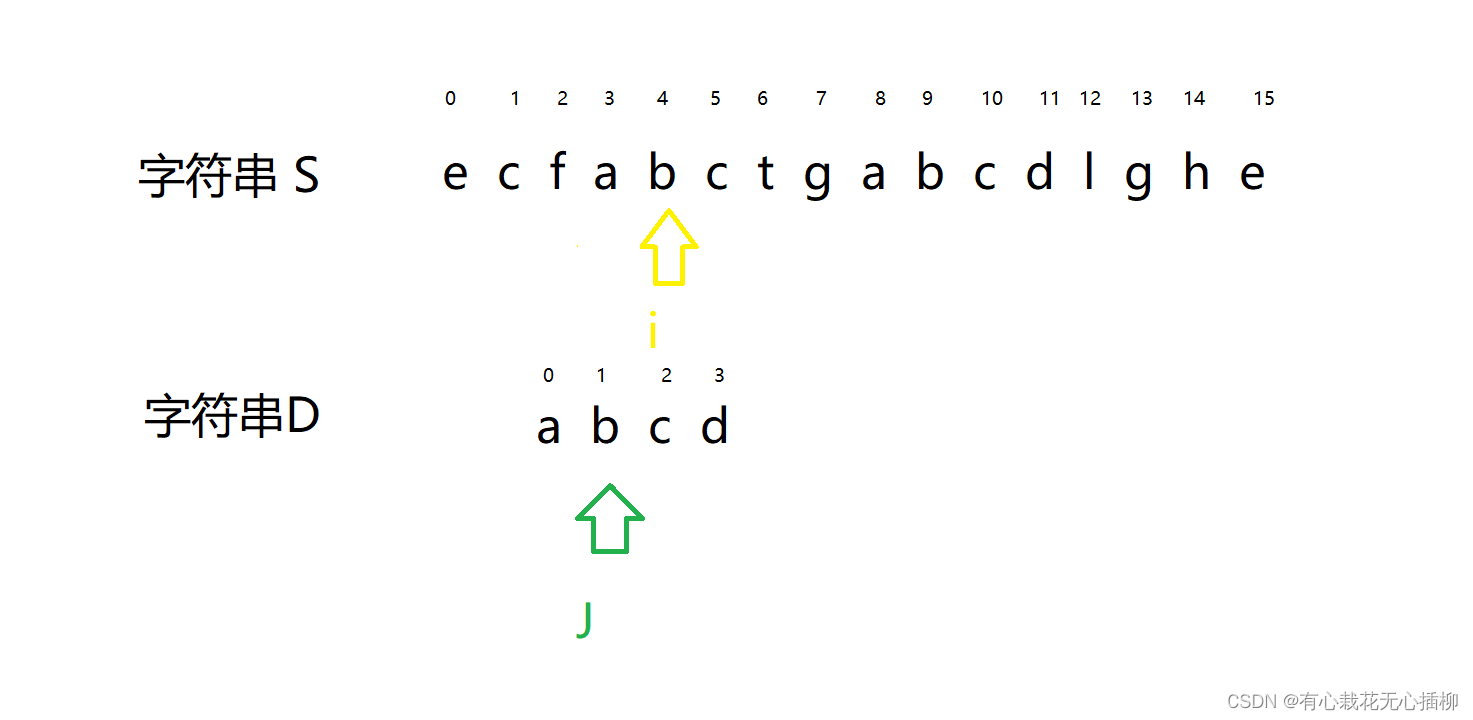
i++ ,j++
i++,j++注意了！ 重点来了- 1
- 2
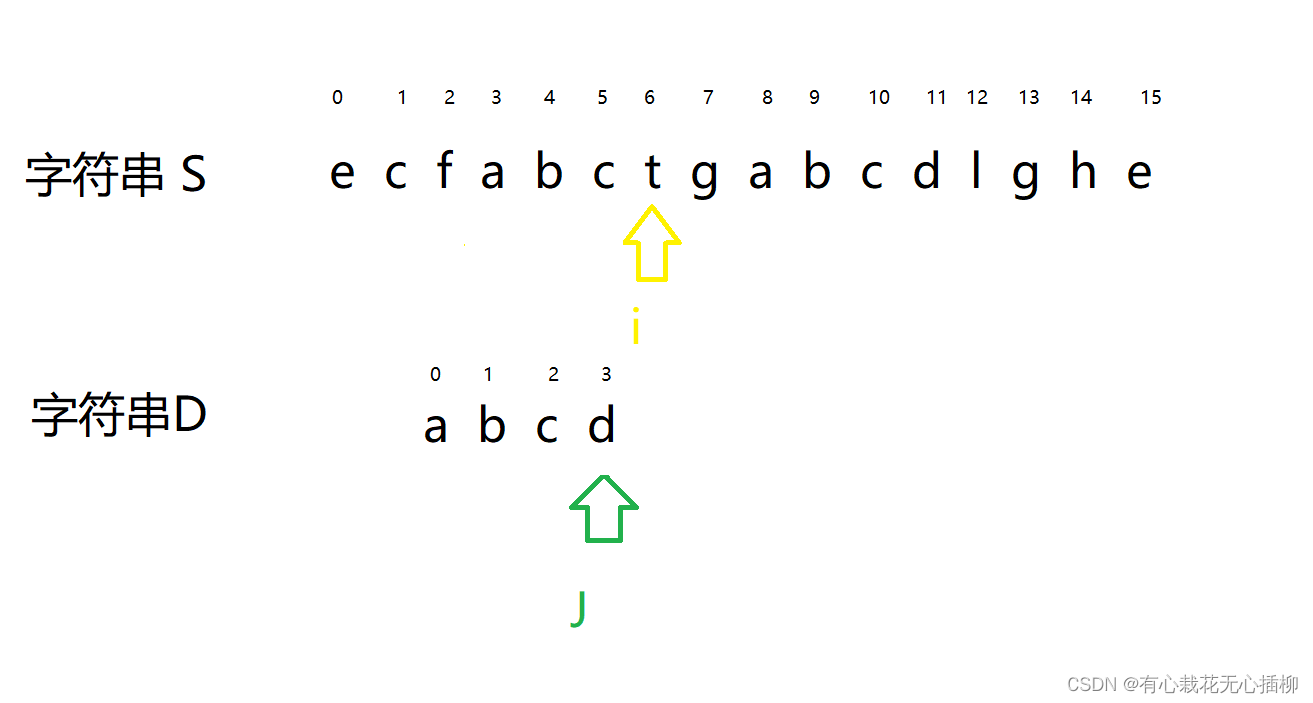
此时 i 和 j 所指向的位置不相等了。 所以 j 要跳回到0位置 那么 i 要跳回到两者开始比较前的后一个位置。 代码怎么写呢？ j = 0 ;这个简单 对于 i 来说，两者比较前的位置是哪？ 是不是 i - j ? 6 - 3 = 3 因为一共走了3步嘛，也就是 j 走的步数。 那么 i 要跳回到两者开始比较前的后一个位置代码就是 i = i - j + 1;- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
然后我们继续比对。- 1
两者跳回到相应位置，继续比对
这里我们 i 一直往后走，都和 j 不一样，我们画图上省略几步。
.
.
.
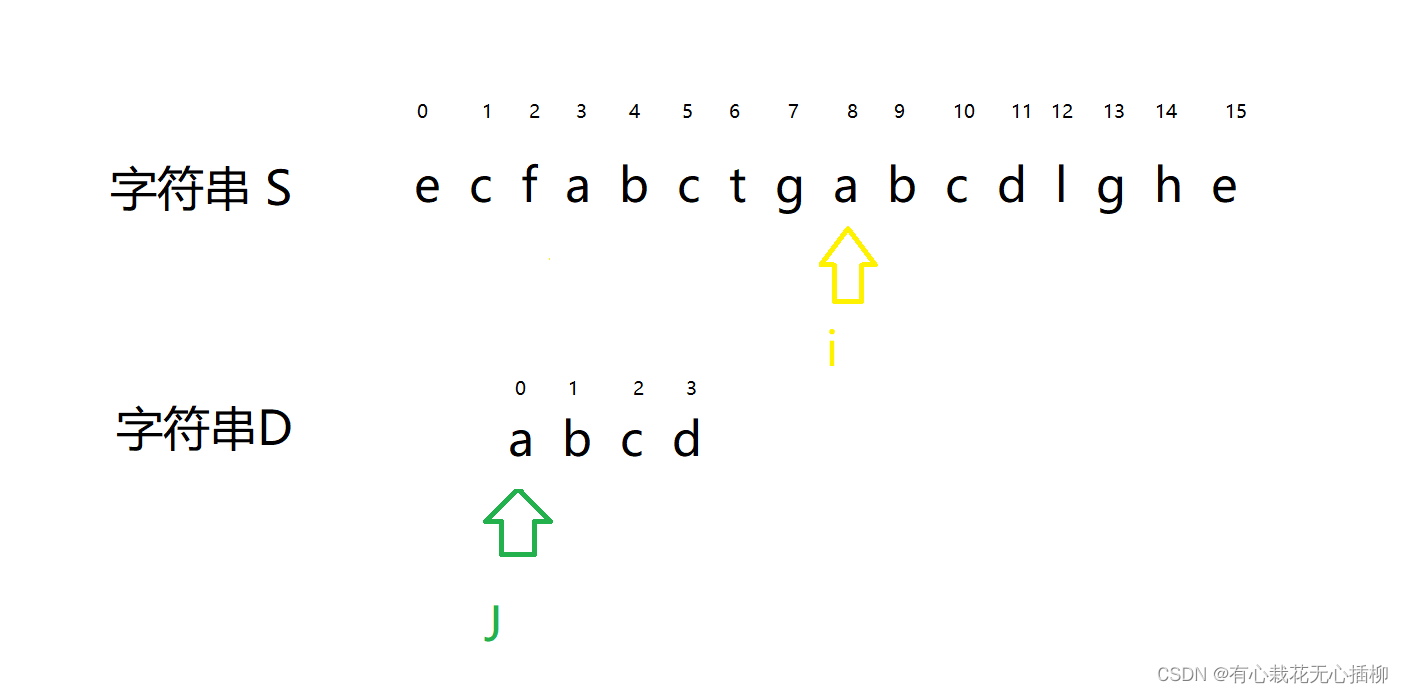
此时 i 和 j 相等了，可以继续比较了。
i++；
j++;
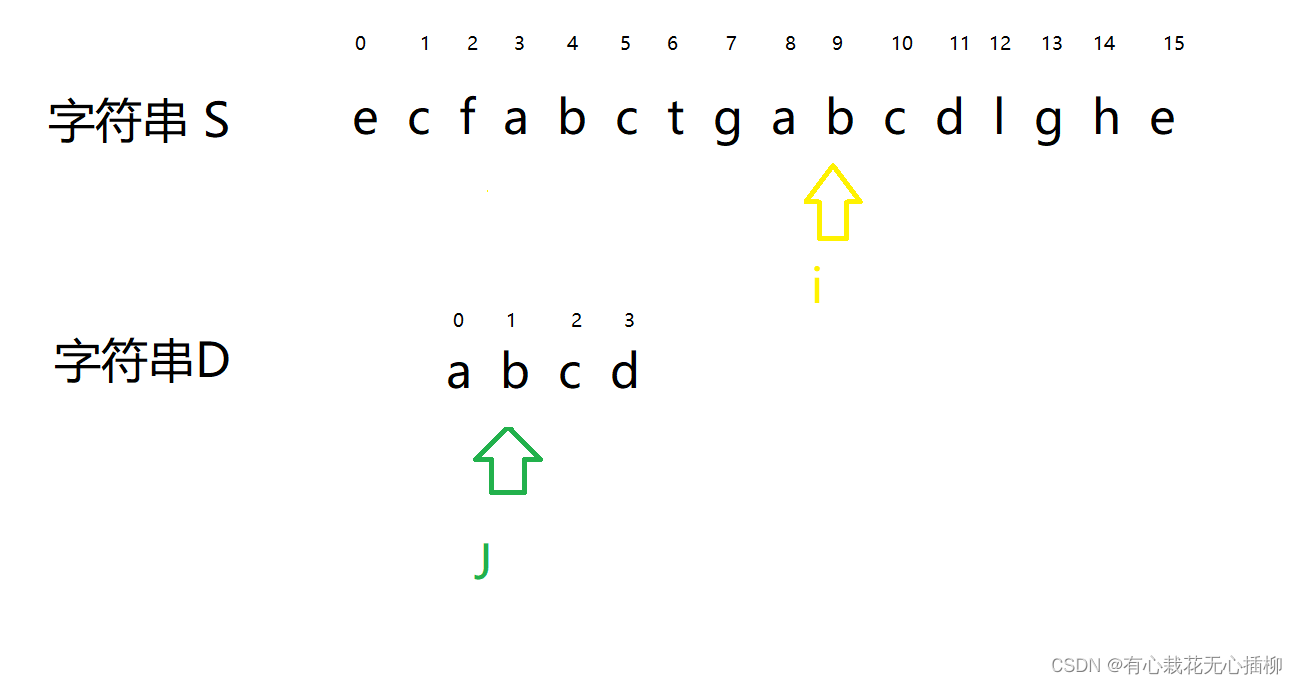
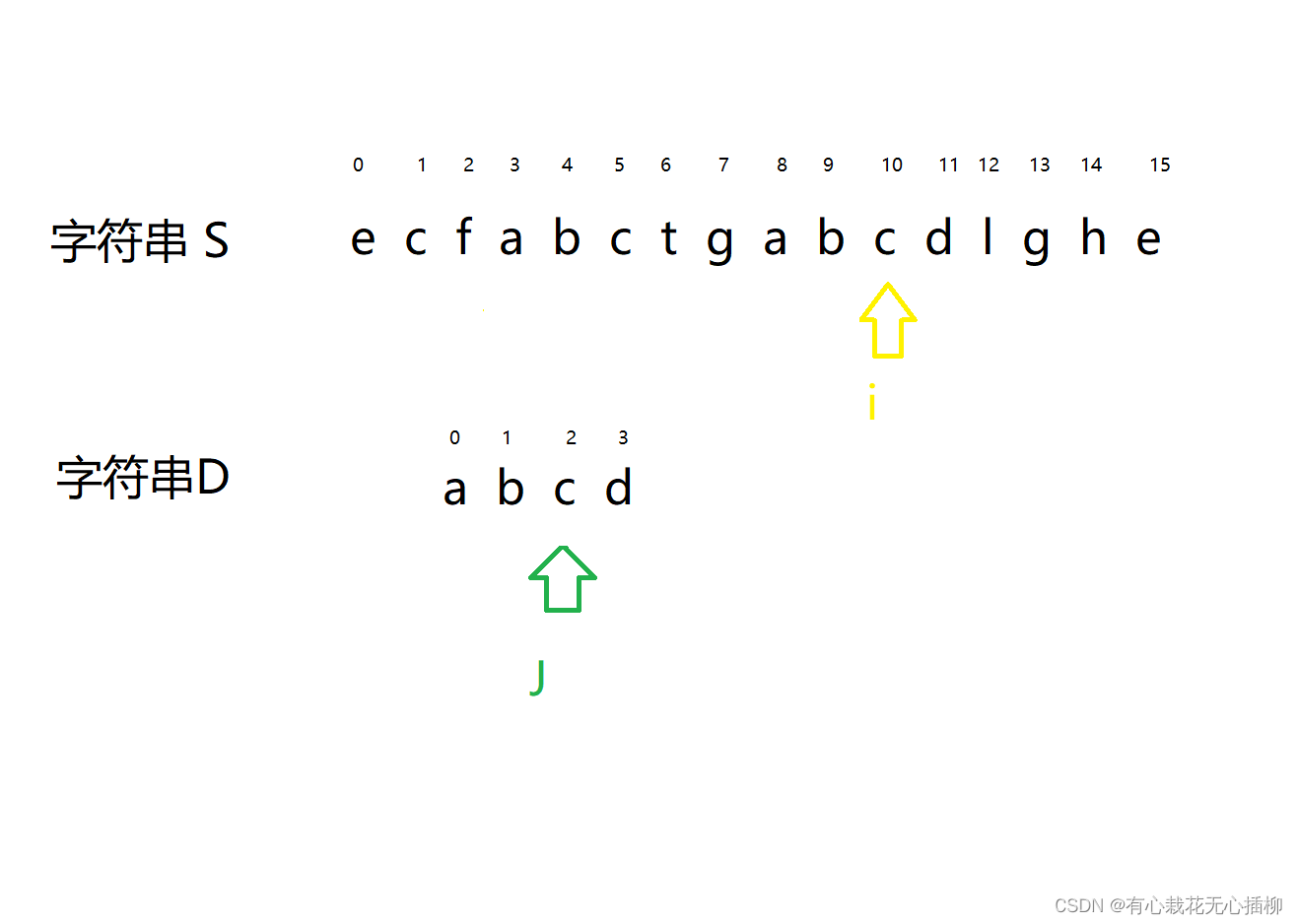
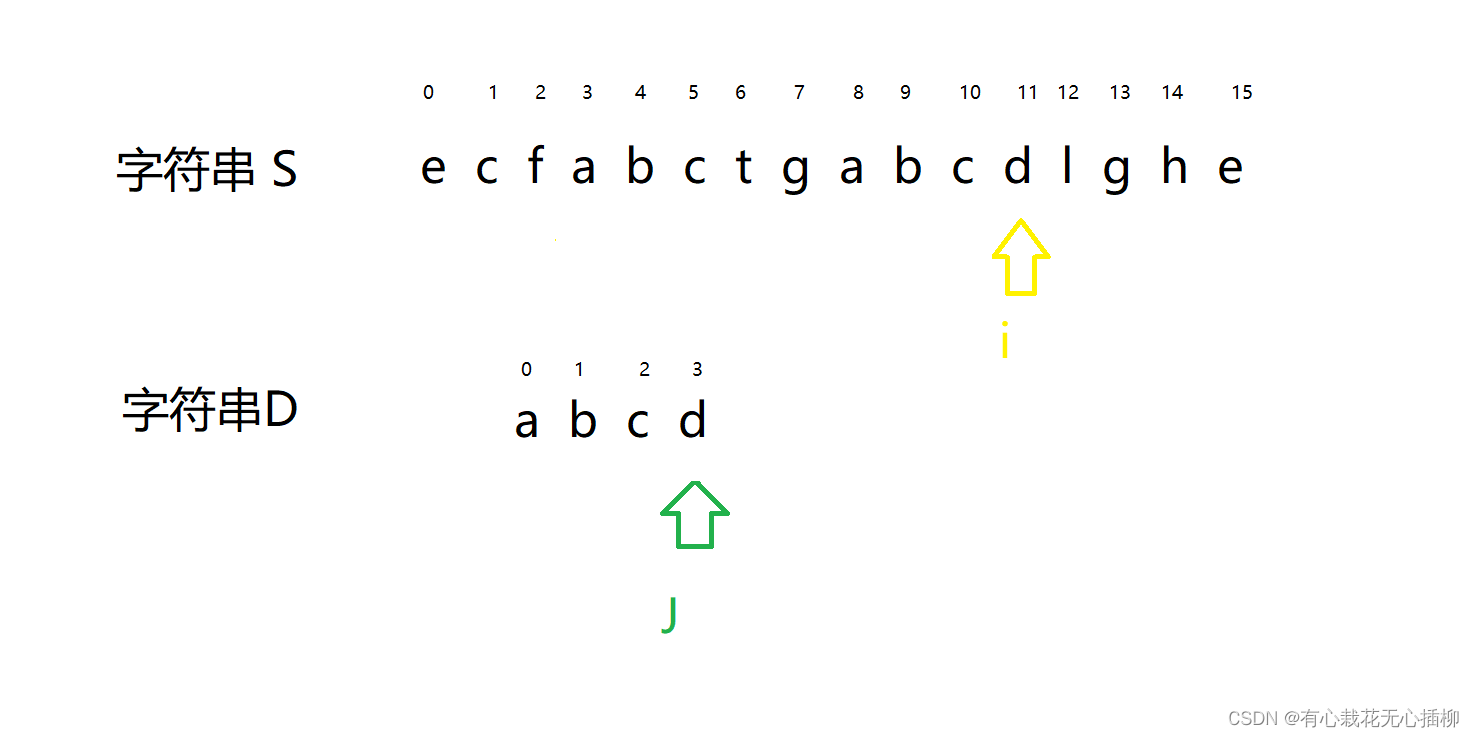
重点又来了！！！ 此时 j 再往后走一步，就说明字符串 D 走完了，说明字符串 S 中包含 D- 1
- 2
此时 J 走完了，那么字符串 S 包含 字符串 D 的起始位置也就是 i - J = 12 - 4;- 1
- 2
到此，字符串 S 包含 字符串 D 情况分析完毕。
.
.
如果字符串 S 不包含字符串 D 会出现什么情况呢？
思考一下，再往下看
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
你的想法不错！
就是 字符串 S 比字符串 D 先走完！这种情况不包含
直接上代码！#include#include #include //BF算法 int BF(const char* source, const char* dest) { assert(source && dest); //断言一下，避免空指针 int len_source = strlen(source); //计算 字符串 S 的长度 int len_dest = strlen(dest); // 计算 字符串 D 的长度 int i = 0, j = 0; //图中的 i 和 j while (i < len_source && j < len_dest) // 当两者其中一个走完时，结束循环 { if (source[i] == dest[j]) // 如果比较的位置字符相等，就继续比较 { i++; j++; } else // 否则 重新开始 比较 { i = i - j + 1; //如果不相等就重新找字符串 S 下一个位置匹配 j = 0; } } // 如果 j 先走完 字符串 D 的长度，就说明字符串 S 中包含 字符串 D if (j >= len_dest) { return i - j; //返回起始位置 } return -1; // 否则返回 -1 } int main() { printf("%d\n", BF("abcdefg", "fg"));//5 printf("%d\n", BF("abcdefg", "fga"));//-1 printf("%d\n", BF("abcdefgabcd", "abcd"));//0 return 0; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
1.3 BF 算法的时间复杂度
BF算法 最坏的情况下,就是未找到 比如 在 字符串S1 :abcabcabcabcf （记录长度为M）中 找 字符串 S2:abcd （记录长度为N） 第1次比较花了 N 次，发现不一样，重新在 S2 第1位比 第2次比较花了 N 次，发现不一样，重新在 S2 第2为比 第M次比较花了N次，发现都不一样， 所以时间复杂度为 O（M * N）- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
2. KMP 算法
KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n) ----------百度百科
上面说的next函数，其实是一个next数组，记住这个next数组，后面有大用！- 1
2.1 KMP 算法和 BF 算法 的区别
首先，要理解 KMP 算法之前，要知道 KMP 和 BF 的区别就是 主串的 i 不会回退，并且 j 也不会回到 0 位置- 1
- 2
2.1.1 为什么主串不回退？
假设上图中在 i = 2 位置处匹配失败了，就算回退到 主串 1 位置也是没有必要的，因为 主串 的1位置处字符也和 子串 0 位置的 a 不一样
再来看下面这张图- 1
第一次匹配时，在 5 位置处 匹配失败了
此时，我们想一想，如果是我们人为移动的话，
j 下一次移动到哪合适？
思考一下
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
答案时 j 移动到 2 位置 处最合适
为什么呢？来分析一下
如果我们按照 BF 的解法，第一次匹配失败，i 要回退到 1 为位置处，
j 要回退到 0 位置处
此时，匹配又失败了。i 到 2 位置处 匹配
又匹配失败了，i 要到 3 位置处匹配
OK，这次 主串 3 位置处 与 子串 0 位置处匹配成功了，比较进行下去
直到这里，又失败了，此时按照 BF 算法 ，i 要回退到 4 位置，j 要回退到0。
好，现在想一下刚才我们问的问题，第一次匹配失败时，如果是我们人为地移动 j 移动到哪合适？
是不是 现在 j 现在 待在的子串 的 2 位置处？
既然我第一次i 和 j 同时 ++ 时匹配失败，第二次 i 和 j 同时 ++ 时匹配也失败了，那么我第二次这个匹配过程是可以省略掉的，就是直接在第一次 i 和 j 同时 ++ 匹配失败时，i 不回退，j 不退回到 0 位置，而是回退这个 2 位置。现在，我们观察一下，这两个字符串。- 1
可以发现这 i 前面的 两个字符，和 子串 0 1两个位置处字符是一样的，
而且 j 既然能走到 5 位置，说明 主串 的 3 4 位置处 和我子串的 3 4 位置也是一样的
而 子串中 括起来的两个方框，长度分别是2，（2 + 2）/ 2 = 2，刚好是我 j 回退的最佳位置
这是不是可能说明这是一个特性，让 j 回退时，回退到这么一个位置就好了呢？当然，这可能也是个巧合，我们继续往下看。我们的目的始终都是: i 不回退，j 回退到一个特定的位置。- 1
既然想让 i 不回退，那么我们就要在主串中找到和子串匹配的一部分。 j 回退到什么位置也是我们要求的- 1
- 2
2. 2 next 数组
还记得 KMP 定义里的next数组吗- 1
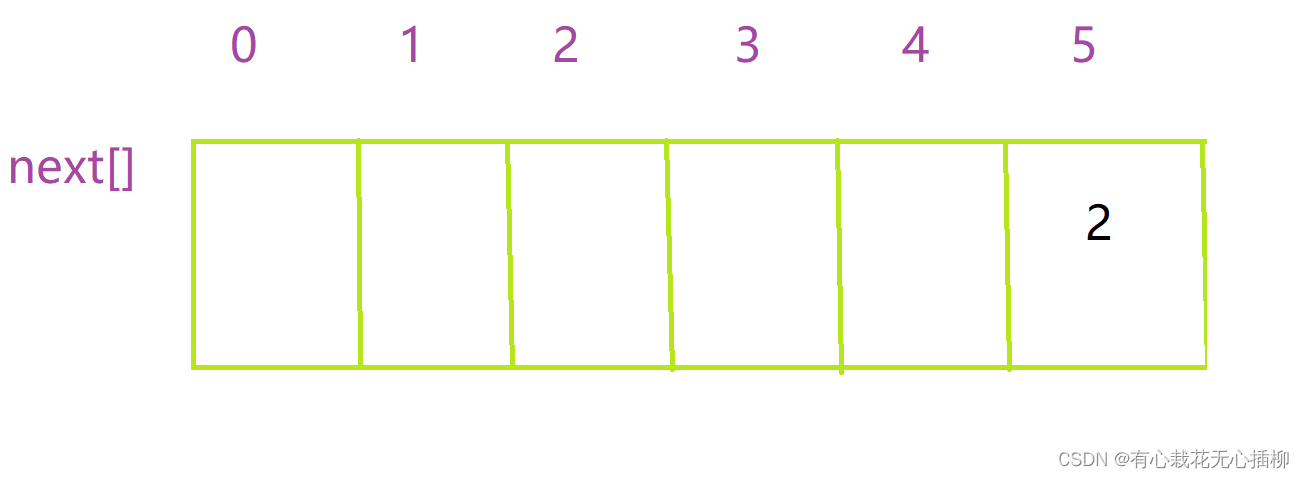
这个next数组里面要存的就是我们 j 在哪个位置匹配失败所要回退的位置， 比如我们刚才在 5 位置处匹配失败，就要回退到 2 位置，记录下来 就是 next[j] = k，k是我们要求的。 现在，直接告诉你结论，k怎么求- 1
- 2
- 3
- 4
1.找到匹配成功部分的两个相等的真子串（不包含本身）长度，一个下标 0 开始，另一个以 j - 1 下标结尾。 2.不管时什么数据，我们规定next[0] = -1;next[1] = 0;- 1
- 2
现在我们来求一下next 数组里各个k 现在我们来求这个子串的next数组- 1
- 2
首先，按照规则，next[0] = -1,next[1] = 0
我们继续求 2 位置时的 k
从 0 位置开始， j - 1 = 2 - 1 = 1 结尾
也就是找从 a 开始，b 结尾两个相等的真子串，
可以看到这是一个子串，不是两个，所以
next[2] = 0;
我们继续求 3 位置的 k
从 0 位置开始，j - 1 = 3 - 1 = 2 结尾
也就是从a 开始，c 结尾两个相等的真子串
可以看到，并不存在，所以
next[3] = 0;
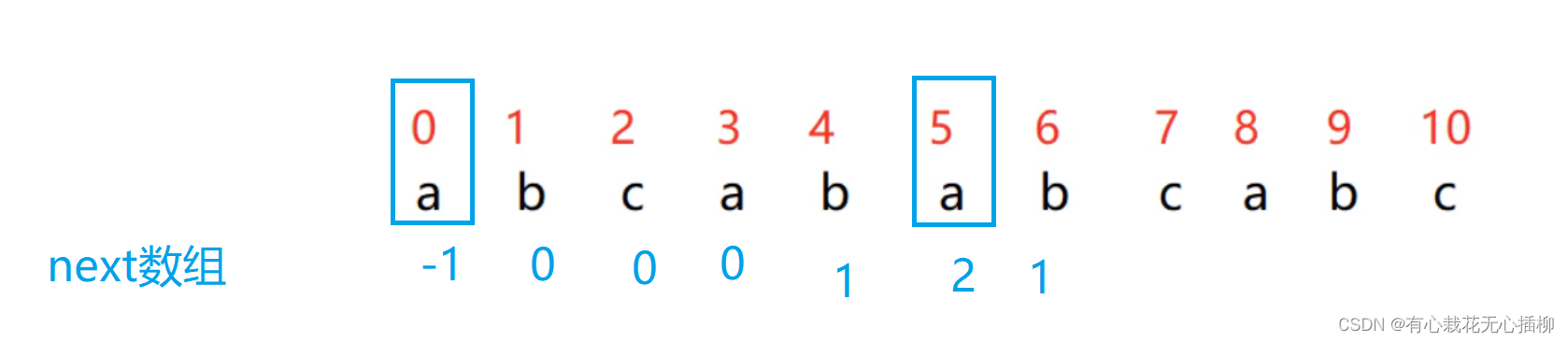
我们继续求 4 位置的 k从 0 位置开始，j - 1 = 4 - 1 = 3 位置结尾 也就是从a 开始，a 结尾的两个相等的真子串 可以看到括起来的部分
前一个自身开始，自身结尾 后一个也自身开始，自身结尾
长度为1，所以next[4] = 1;
我们继续求 5 位置的 k
找 a 开始 b 结尾的两个相等的真子串
长度为 2 ，所以
next[5] = 2;
我们继续求 6 位置的 k
找 a 开始，a 结尾的两个相等的真字串
长度为1
所以next[6] = 1;
我们继续求 7 位置的 k
找 a 开始 ，a 结尾的两个相等的真子串
长度为 2
所以 next[7] = 2
我们继续求 8 位置的 k
找从 a 开始 c 结尾的两个相等的真子串
长度为3
所以 next[8] = 3
我们继续求 9 位置的 k
找 从a 开始 a 结尾的两个相等的真子串
长度为4
所以next[9] = 4
我们继续求 10 位置的 k
找从 a 开始 b 结尾的两个相等的真子串
长度为 5
所以next[10] = 5
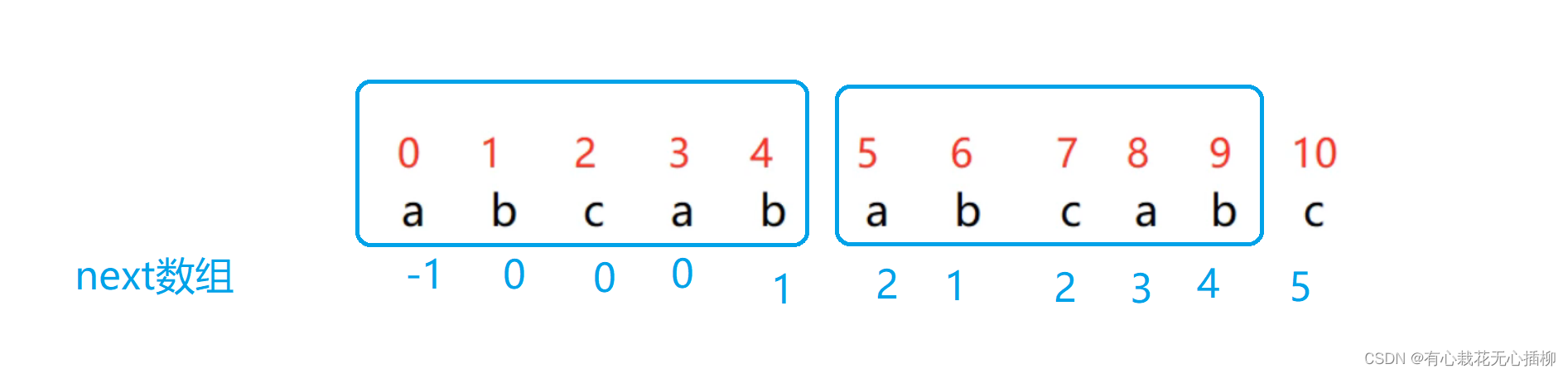
next 数组我们就求完了。 记住next数组里求的是我们 在位置 j 处匹配失败时要退回的 k 处- 1
- 2
上面的方法都是我们手动去求的 那我们在代码上怎么体现？ 先不急着看代码，我们分析一下- 1
- 2
- 3
现在假设我们next[j] = k;
就是 j 位置匹配失败时，我们 j 要退回到 k 处J 现在在 8 位置处，我们求 9 位置为什么等于 next[9] = 4?- 1
如下图分析一下，
8 位置处，我们的 k = 3
是不是说明了刚才我们求的时候
从a 开始 c 结尾的两个相等的真子串就是我们下面画横线的两个
我们肉眼看可以看出来。
也就是说，有这么一个公式
p[0]~p[k-1] = p[x]~p[j-1]......（1） 表示第0个位置到第k-1个位置的字符 等于 第x到第j-1个位置的字符 这个x是我们要求的- 1
- 2
- 3
按照上面的公式，我们求一下x 利用数组之间的长度 k - 1 - 0 = j - 1 - x; 可以轻易得出 x = j - k;......(2) 所以 将（2）代入（1）， 得 p[0]~p[k-1] = p[j-k]~p[j-1] ......(3) 代入验证一下 p[0]~p[2] = p[5]~p[7],正确！！！- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
我们回过来，我们要求的是 9 位置为什么 k = 4- 1
再假设，如果 p[k] = p[j] ......(4) 那么由（3），就可以有 p[0]~p[k] = p[j-k]~p[j]......(5)- 1
- 2
- 3
我们一开始假设 k = next[j] 对应了p[0]~p[k-1] = p[j-k]~p[j-1]; ......(3) 那么刚才推出来的 p[0]~p[k] = p[j-k]~p[j] ......(5) 可以对应 k + 1 = next[j + 1]- 1
- 2
- 3
- 4
- 5
- 6
- 7
也就是说，有了 next[i] = k 和 p[k] = p[j] 这两个假设 那么就能对应出 k + 1 = next[j+1] 我们要求的 9 的位置为什么是 4 也就求出来了。 因为p[3] = p[8] = a; 所以 3 + 1 = next[ 8 + 1] 所以next[9] = 4- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
那如果 p[j] != p[k] 我们的 next[i+1] 怎么求呢？ 看一下下面这个例子- 1
- 2
- 3
此时p[j] != p[k]
我们的 next [6] = 1 怎么求呢？
既然我们 p[j] = p[k] 才能求出下一位，我们就想办法让 p[j] != p[k] 让它变成 p[j] = p[k] 怎么变？ 思考一下。就两个字。 . . . . . . . . . . . . . . . . . 答案是 回退！- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
next[2] = 0,那我们就回退到 0 位置
此时 p[k] = p[j] 所以满足我们要的条件了， 所以 next[j + 1] = k + 1 next[5 + 1] = 0 + 1 = 1; next[6] = 1 可以求出来了！！！- 1
- 2
- 3
- 4
- 5
- 6
2.2.3 next数组总结
总结一下 1.当 p[k] = p[j] 时 可以直接求next[j+1] = k + 1 2.当p[k] != p[j] 时 我们就回退！ 回退到 p[k] = p[j] 为止- 1
- 2
- 3
- 4
- 5
- 6
- 7
3.代码
3.1 伪代码分析
先看一下伪代码- 1
//和上面的BF算法代码，差不多类似。 //先不管next数组怎么求 int KMP(const char* source, const char* dest,int pop) { // source 表示主串，dest表示子串，pop表示从母串哪个位置开始求，一般为0位置 assert(source && dest);//防止空指针 int len_source = strlen(source);//计算长度 int len_dest = strlen(dest); int i = pop; // 遍历主串 int j = 0;//遍历子串 while (i < len_source && j < len_dest) { if (j == -1 || source[i] == dest[j]) { i++; j++; } else { j = next[j]; } } if (j >= len_dest) // 当子串先走完说明主串包含子串，返回位置 { //不明白i - j的可以看看上面的BF算法分析 return i - j; } return -1; //否则说明不主串不包含子串，返回-1 }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
//看一下这段代码 if (j == -1 || source[i] == dest[j]) { i++; j++; } else { j = next[j]; } //source[i] == dest[j] 就是上来先比较一下，都一样就继续往后比 // j == -1 什么意思？ //就是当子串dest[0] ！= source[0]; //进入else //那么 j = next[0] = -1; //而 j = -1 会导致数组越界，所以我们要加上 j == -1 时j++- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
3.2 求 next 数组
//先malloc一下next数组 int* next = (int*)malloc(sizeof(int) * len_dest);- 1
- 2
//再写求next的函数 //注意，这里的写法和我们刚才分析的有所差异 //但是大体思路一样 void GetNext(int* next, const char* dest) { int len_dest = strlen(dest); next[0] = -1; next[1] = 0; int j = 2;//当前j 下标 int k = 0; //前一项的k while (j < len_dest) { if((k == -1) || dest[k] == dest[j - 1]) { next[j] = k + 1; j++; k++; } else { k = next[k]; } } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
//看一下这段代码 if((k == -1) || dest[k] == dest[j - 1]) { next[j] = k + 1; j++; k++; } else { k = next[k]; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
j 从 2 位置开始
我们刚才分析的时候，如下图
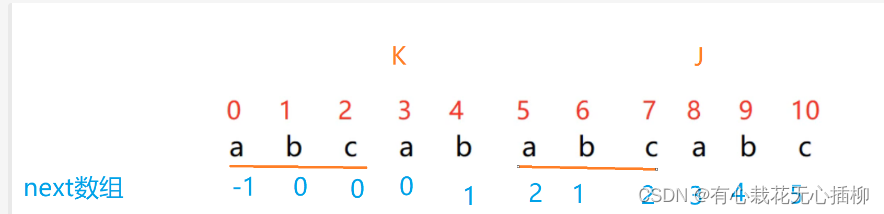
我们是知道了，j 下标， 才得出 p[j] = p[k] 才知道了 next[j + 1] = k + 1; 而我们这里- 1
- 2
- 3
- 4
- 5
- 6
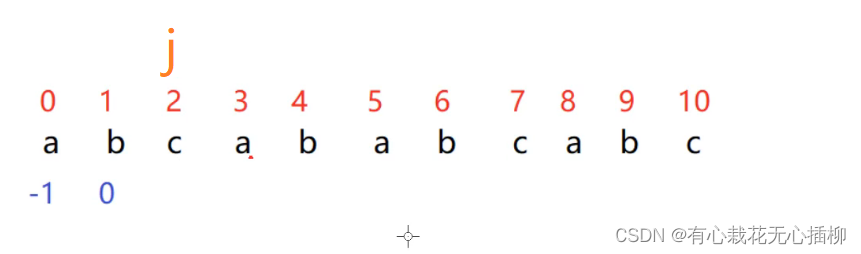
j 是没求的
所以相当于我们求的是 j - 1 下标
所以我们现在的 j 相等于原来的 j + 1之前分析的图（如下图）相对于我们现在要求的图来说是这样的
我们还不知道next[8] = 3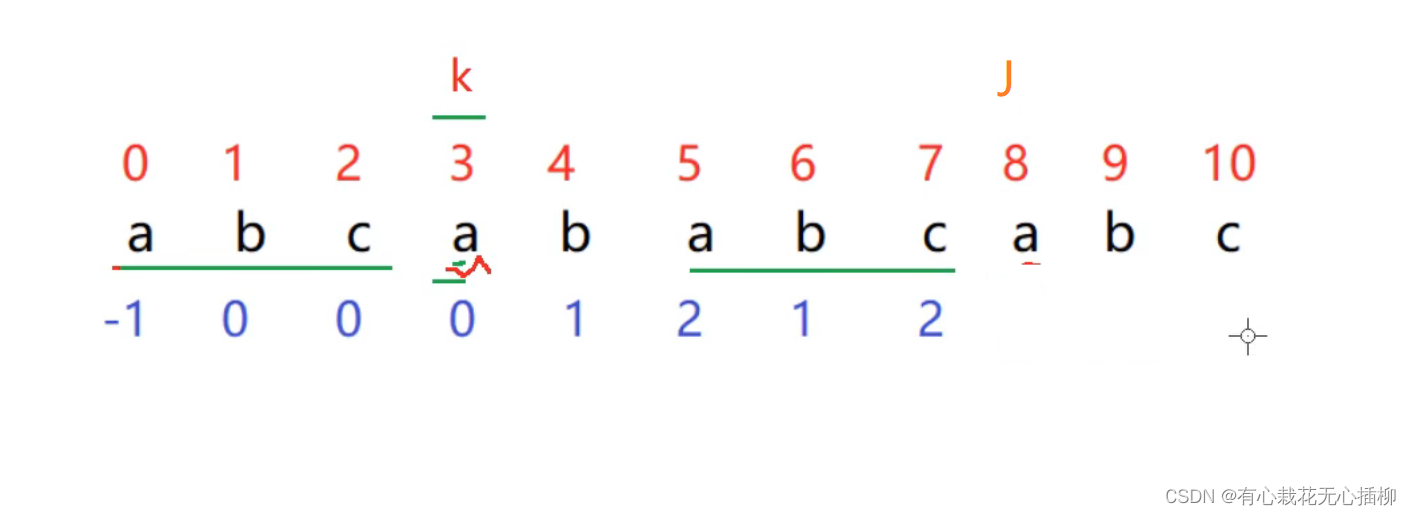
所以相当于 p[j - 1] = p[k] 所以p[8-1] = p[k] p[7] = p[k] ，现在 k 在位置2上 所以p[7] = p[2] = 'c' 也就是说next[j] = k + 1;- 1
- 2
- 3
- 4
- 5
所以公式由原来的 p[j] = p[k] 变成了 p[j - 1] = p[k] 所以next[j] = k + 1;- 1
- 2
- 3
int j = 2;//当前j 下标 int k = 0; //前一项的k- 1
- 2
void GetNext(int* next, const char* dest) { int len_dest = strlen(dest); next[0] = -1; next[1] = 0; int j = 2;//当前j下标 int k = 0; //前一项的k while (j < len_dest) { //满足dest[k] = dest[j-1]就进来 if((k == -1) || dest[k] == dest[j - 1]) { next[j] = k + 1; // 如刚才分析的那样 j++; k++; } else //否则就回退，注意回退的时候是有可能退到-1的 //因为next[0] = -1,所以上面的if语句有 k == -1时就进来k++; //所以某一个位置上 next[j] = -1 + 1 = 0; { k = next[k]; } } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
3.2.1 next数组的优化
我们的next数组还能再次优化，来看下面这个例子
当我的 j 在 5 位置处匹配失败，是不是要根据最下面的next数组，是不是要先回退到 4 位置，如何到了 4 位置要 回退到 3 位置，然后一直回退一直回退，到 0 位置，回退 -1 位置。
那我能不能一步回退到 -1？
优化后如下
while ( i < len_dest) { if (dest[i] == dest[next[i]]) { next[i] = next[next[i]]; } i++; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
4. 完整代码
//KMP算法 void GetNext(int* next, const char* dest) { int len_dest = strlen(dest); next[0] = -1; next[1] = 0; int j = 2;//当前j下标 int k = 0; //前一项的k while (j < len_dest) { //满足dest[k] = dest[j-1]就进来 if ((k == -1) || dest[k] == dest[j - 1]) { next[j] = k + 1; // 如刚才分析的那样 j++; k++; } else //否则就回退，注意回退的时候是有可能退到-1的 //因为next[0] = -1,所以上面的if语句有 k == -1时就进来k++; //所以某一个位置上 next[j] = -1 + 1 = 0; { k = next[k]; } } int i = 2; while ( i < len_dest) // 优化next数组 { //如果回退的位置和当前位置的字符一样 if (dest[i] == dest[next[i]]) { //就写回退位置那个next值 next[i] = next[next[i]]; } i++; } } // source 表示主串，dest表示子串，pop表示从母串哪个位置开始求，一般为0位置 int KMP(const char* source, const char* dest,int pop) { assert(source && dest); int len_source = strlen(source); int len_dest = strlen(dest); int i = pop; // 遍历主串 int j = 0;//遍历子串 int* next = (int*)malloc(sizeof(int) * len_dest); GetNext(next, dest); while (i < len_source && j < len_dest) { if ((j == -1) || source[i] == dest[j]) { i++; j++; } else { j = next[j]; } } //source[i] == dest[j] 就是上来先比较一下，都一样就继续往后比 // j == -1 什么意思？ //就是当子串dest[0] ！= source[0]; //进入else //那么 j = next[0] = -1; //而 j = -1 会导致数组越界，所以我们要加上 j == -1 时j++ if (j >= len_dest) { return i - j; //如果子串先走完，说明主串包含子串，返回 i - j的位置 } //不明白的可以看看上面BF算法分析 return -1; }//否则说明主串不包含子串，返回 -1 int main() { printf("%d\n", KMP("rgabcdkkk", "abcd", 0)); // 2 printf("%d\n", KMP("rgabcdkkk", "r", 0)); // 0 printf("%d\n", KMP("rgabcdkkk", "kg", 0)); // -1 return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
-
相关阅读:
LeetCode 周赛上分之旅 #45 精妙的 O(lgn) 扫描算法与树上 DP 问题
计算机的组成
【c语言】指针和数组笔试题
一篇文章带你掌握测试基础语言——Python
71页文档统一管理云平台项目建设方案
长安区块链：服务器时间不一致导致调用合约失败
微信小程序对接发货功能
练习八-利用有限状态机进行时序逻辑的设计
C# OpenCvSharp 基于直线检测的文本图像倾斜校正
android存储，内部存储，外部存储，日志
- 原文地址：https://blog.csdn.net/iamxiaobai_/article/details/127584904
