【牛客刷题专栏】0x09:C数据结构合并两个排序的链表

前言

• 个人推荐在牛客网刷题(点击可以跳转)，它登陆后会保存刷题记录进度，重新登录时写过的题目代码不会丢失。
• 个人刷题练习系列专栏：个人CSDN牛客刷题专栏。 牛客数据结构题目位置如下：
  

---

问题描述：

• 输入两个递增的链表，单个链表的长度为n，合并这两个链表并使新链表中的节点仍然是递增排序的。
  数据范围：0≤n≤1000，-1000 \le 节点值0≤节点值≤1000
• 要求：空间复杂度 O(1)，时间复杂度 O(n)
• 如输入{1,3,5},{2,4,6}时，合并后的链表为{1,2,3,4,5,6}，所以对应的输出为{1,2,3,4,5,6}，转换过程如下图所示：
  
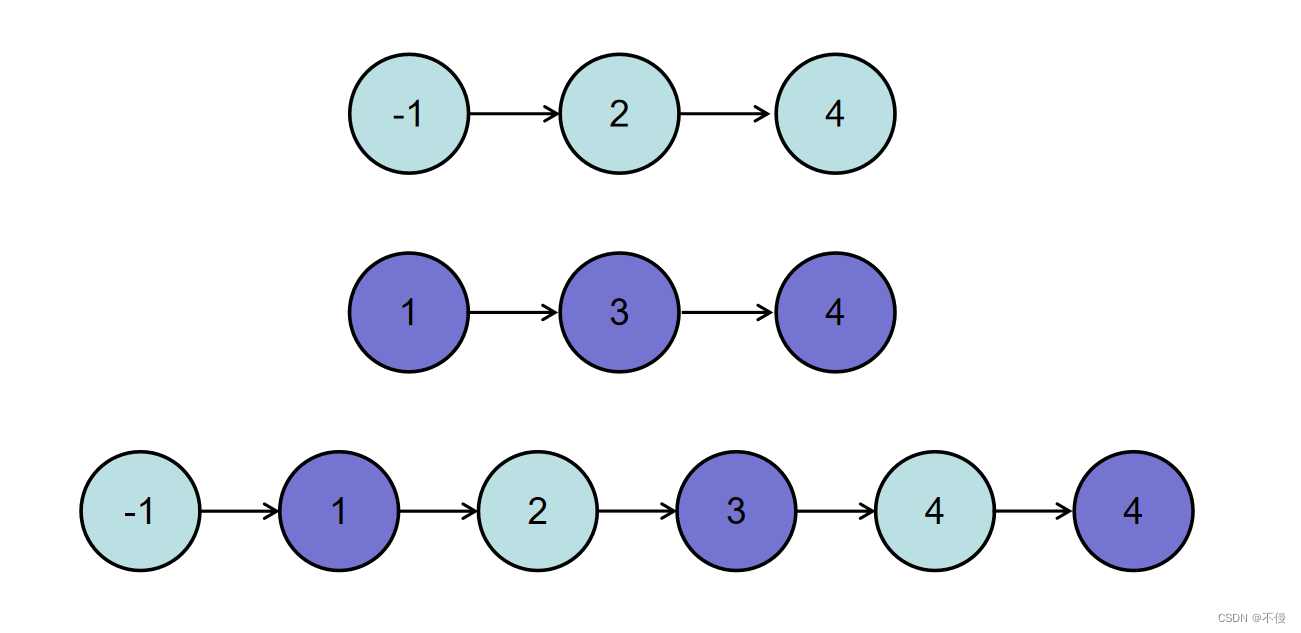
• 或输入{-1,2,4},{1,3,4}时，合并后的链表为{-1,1,2,3,4,4}，所以对应的输出为{-1,1,2,3,4,4}，转换过程如下图所示：
  

---

举例：

//例1：
//输入：
{1,3,5},{2,4,6}
//返回值：
{1,2,3,4,5,6}
//============
//例2：
//输入：
{},{}
//返回值：
{}
//例3：
//输入：
{-1,2,4},{1,3,4}
//返回值：
{-1,1,2,3,4,4}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

---

解法思路：

• 由于输入的两个递增的链表，则无需对各自进行排序，只需从各自第一个数据开始，取较小的往新链表内存放即可。

---

代码结果：

/**
 * struct ListNode {
 *	int val;
 *	struct ListNode *next;
 * };
 */

/**
 * @param pHead1 ListNode类 
 * @param pHead2 ListNode类 
 * @return ListNode类
 */
struct ListNode* Merge(struct ListNode* pHead1, struct ListNode* pHead2 ) 
{
    struct ListNode* vhead = (struct ListNode*)malloc(sizeof(struct ListNode)); //新建一个头结点
    vhead->val = -1;
    struct ListNode *p = vhead;   //用一个指针指向该头结点
        while (pHead1 && pHead2)    //两个链表都未比较完
       {
            if (pHead1->val <= pHead2->val) //表1的值更小
           {
                p->next = pHead1;    //先将结点连接到新表，再让原表指针后移一位，二者顺序不可换
                pHead1 = pHead1->next;
            }
            else {
                p->next = pHead2;
                pHead2 = pHead2->next;
            }
            p = p->next;  //加入一个新结点后，新表指针也后移一位
        }
        p->next = pHead1 ? pHead1 : pHead2;  //都比较完后，哪个表非空则直接加入到新表中
        return vhead->next;  //返回第一个结点
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

---

---

结束语

• 以上就是C数据结构合并两个排序的链表的内容。可以在牛客尝试刷几道题目来练习实践。牛客网刷题(点击可以跳转)，可以尝试注册使用。