-
机器学习的python编程基础
一、回归
训练数据集click.csv如下:
x,y 235,591 216,539 148,413 35,310 85,308 204,519 49,325 25,332 25,332 173,498 191,498 134,392 99,334 117,385 112,387 162,425 272,659 159,427 59,319 198,522- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
我们的目的是从该数据集中发现一种规律,通过该规律我们可以根据任意给定的y值,预测出x的值。这个过程也被称为学习。
首先我们把这些点在二维坐标系中显示出来,通过图像可以更加直观的发现数据的分布规律。import numpy as np import matplotlib.pyplot as plt # 读入训练数据 train = np.loadtxt('click.csv',delimiter=',',skiprows=1) train_x = train[:,0] train_y = train[:,1] # 绘图 plt.plot(train_x,train_y,'o') plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
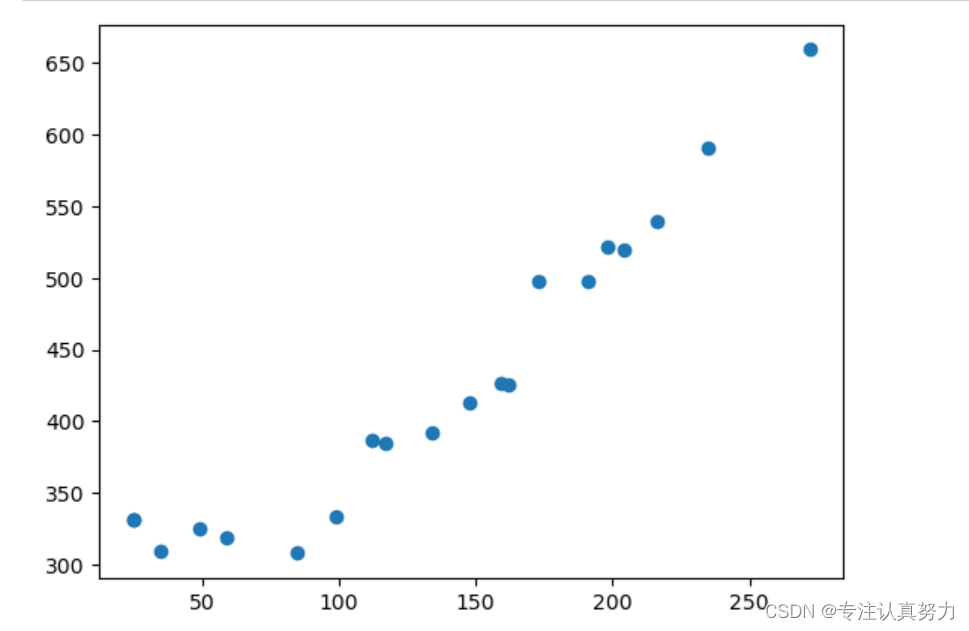
我们把这个数据集的要学习的规律称为fθ(x)。首先把fθ(x)作为一次函数来实现吧。我们要实现下面这样的fθ(x)和目标函数E(θ)。
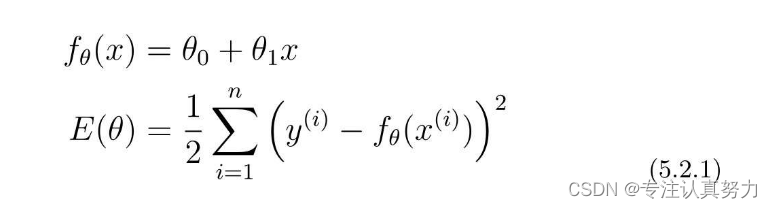 对进行θ0和θ1的初始化,用随机值作初始值。
对进行θ0和θ1的初始化,用随机值作初始值。# 参数初始化 theta0 = np.random.rand() theta1 = np.random.rand() # 预测函数 def f(x): return theta0+theta1*x # 目标函数 def E(x,y): return 0.5*sum((y-f(x))**2)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
对训练数据进行预处理:把训练数据变成平均值为0、方差为1的数据。
这个预处理不是必须的,但是做了之后,参数的收敛会更快。这种做法也被称为标准化或者z-score规范化,变换表达式是这样的。µ是训练数据的平均值,σ是标准差。

# 标准化 mu = train_x.mean() sigma = train_x.std() def standardize(x): return (x-mu)/sigma train_z = standardize(train_x) plt.plot(train_z,train_y,'o') plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
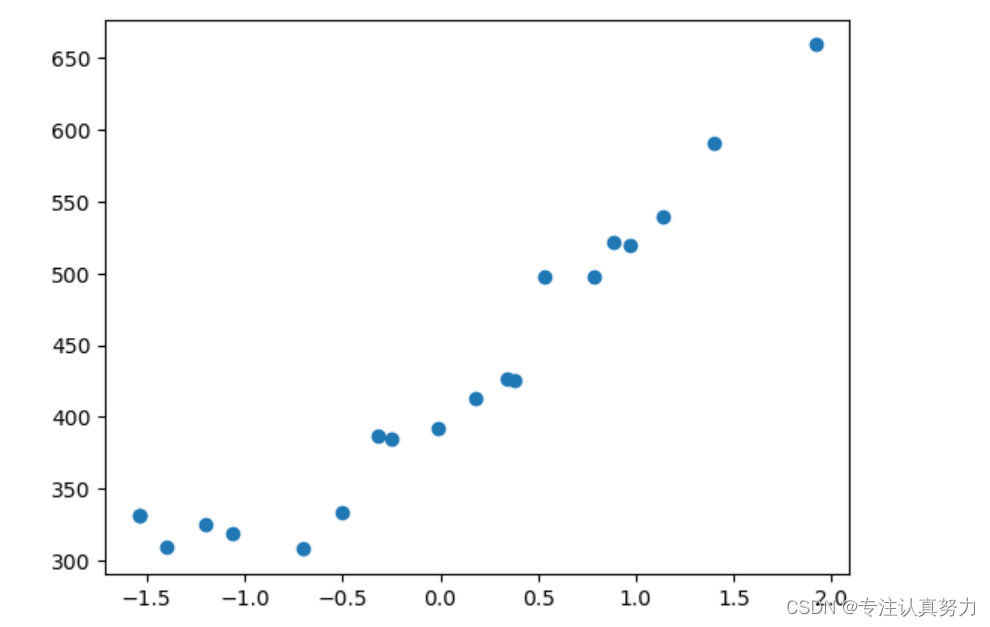
可以发现经过标准化后横轴的刻度变小了。接下来就是去寻找fθ(x)的规律,由于我们假设该数据集具有一次函数的规律。对于一次函数,我们需要从数据集中得到两个参数θ0、θ1,使其能够尽可能经过数据集的所有点。
利用梯度下降的方法去寻找使误差函数E(θ)最小的两个参数。
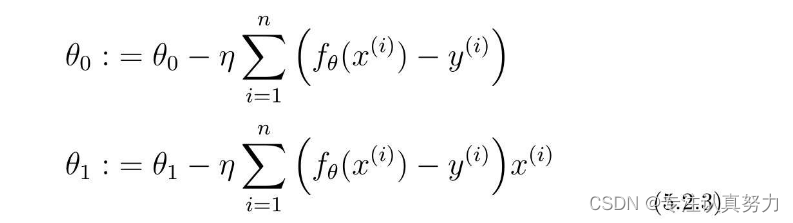
# 学习率 ETA = 1e-3 # 误差的差值 diff = 1 # 更新次数 count = 0 # 重复学习 error = E(train_z,train_y) while diff > 1e-4: # 更新结果保存到临时变量 tmp0 = theta0 - ETA*np.sum((f(train_z)-train_y)) tmp1 = theta1 - ETA*np.sum((f(train_z)-train_y)*train_z) # 更新参数 theta0 = tmp0 theta1 = tmp1 # 计算与上一次的差值 current_error = E(train_z,train_y) diff = error - current_error error = current_error # 输出日志 count += 1 log = '第{}次:theta0={:.3f},theta1={:.3f},差值={:.4f}' print(log.format(count,theta0,theta1,diff))- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
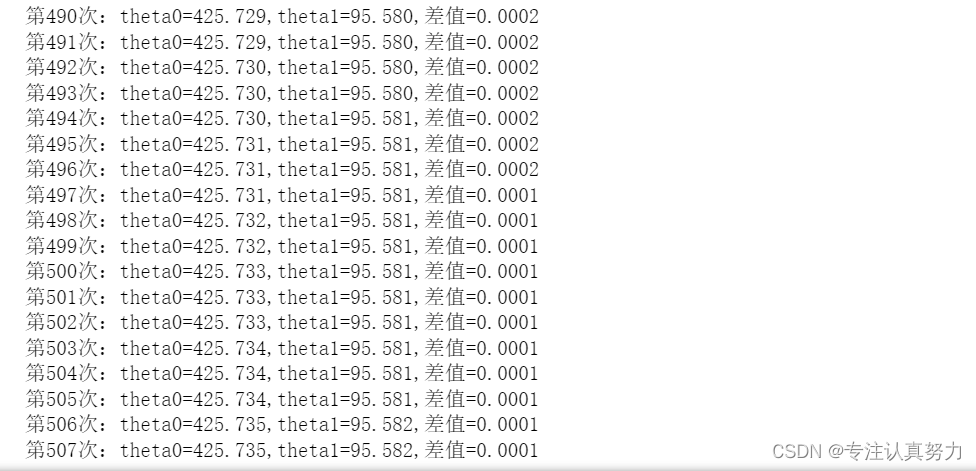
# 绘图确认 x = np.linspace(-3,3,100) plt.plot(train_z,train_y,'o') plt.plot(x,f(x)) plt.show()- 1
- 2
- 3
- 4
- 5
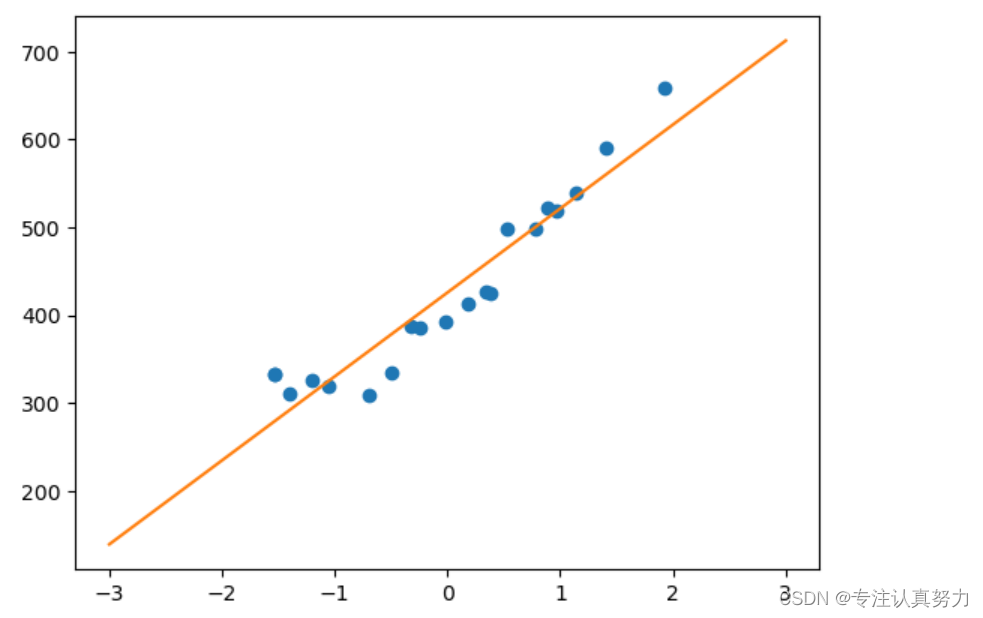
前面我们假设数据集中的规律为一次函数,并对其成功进行了拟合。实际上,我们也可以假设规律为二次函数。
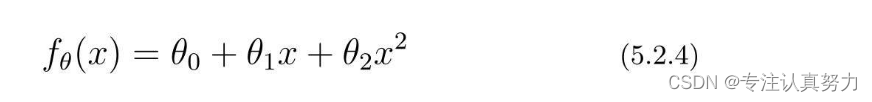
将参数和训练数据都作为向量来处理,可以使计算变得更简单。
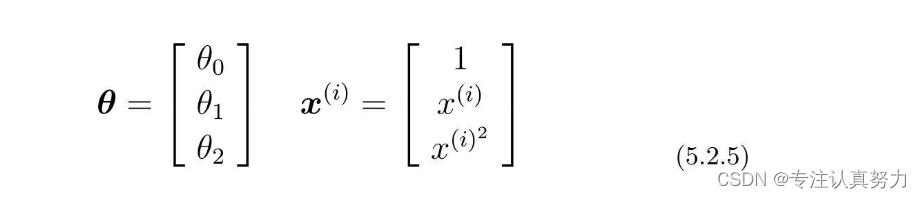
不过由于训练数据有很多,所以我们把1行数据当作1个训练数据,以矩阵的形式来处理会更好。
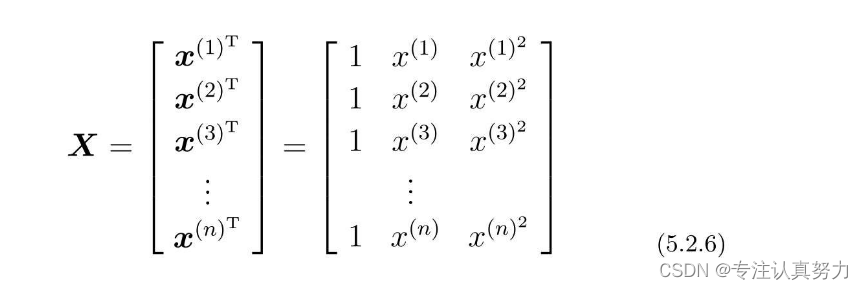
然后,再求这个矩阵与参数向量θ的积。
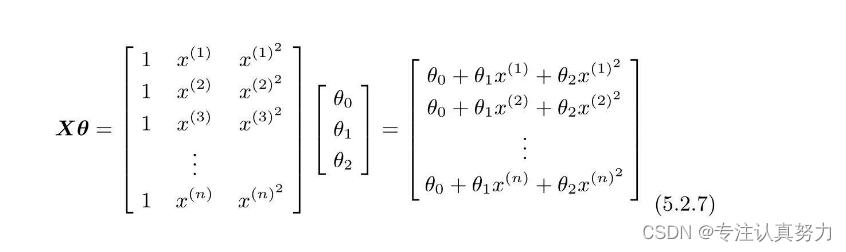
# 初始化参数 theta = np.random.rand(3) # 创建训练数据的矩阵 def to_matrix(x): return np.vstack([np.ones(x.shape[0]),x,x ** 2]).T X = to_matrix(train_z) # 预测函数 def f(x): return np.dot(x,theta) # 误差的差值 diff = 1 # 重复学习 error = E(X,train_y) while diff > 1e-3: # 更新参数 theta = theta - ETA * np.dot(f(X)-train_y,X) # 计算与上一次误差的差值 current_error = E(X,train_y) diff = error -current_error error = current_error x = np.linspace(-3,3,100) plt.plot(train_z,train_y,'o') plt.plot(x,f(to_matrix(x))) plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
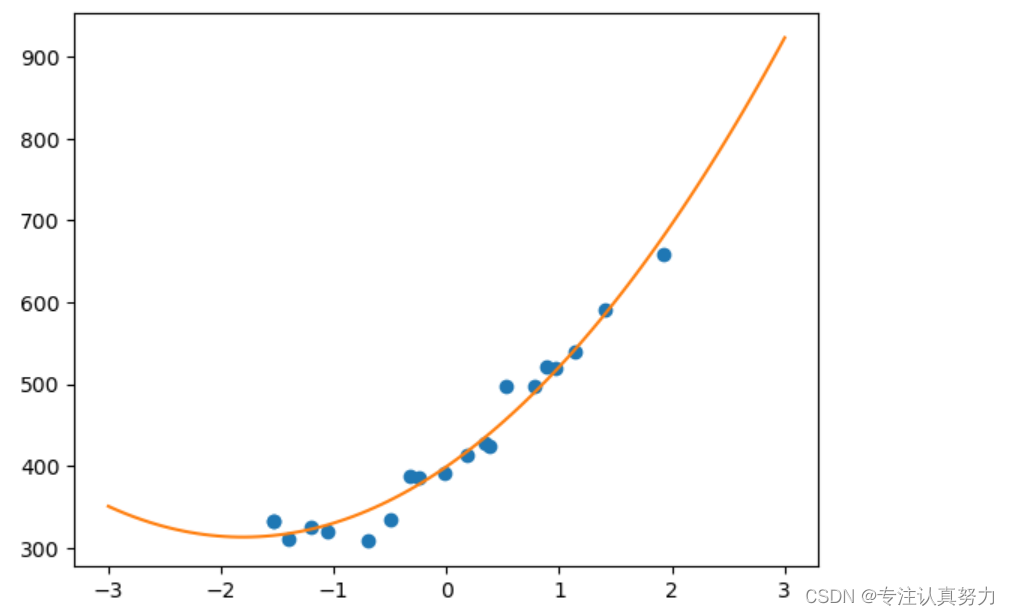
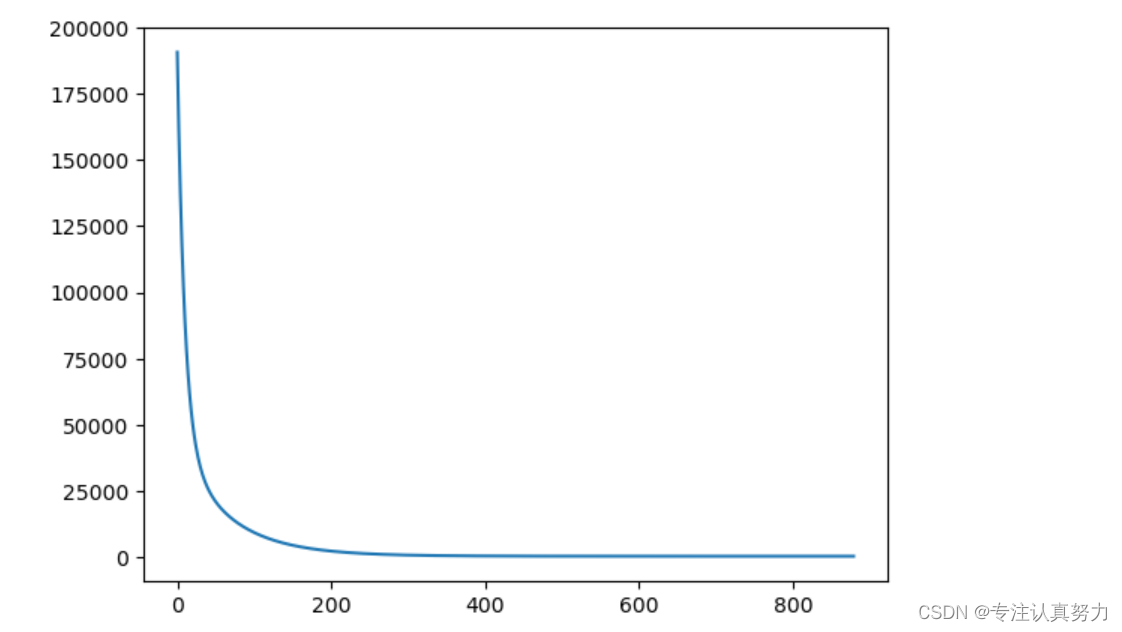
# 均方误差 def MSE(x,y): return (1 / x.shape[0]) * np.sum((y-f(x))**2) # 用随机值初始化参数 theta = np.random.rand(3) # 均方误差的历史记录 errors = [] # 误差的差值 diff = 1 # 重复学习 errors.append(MSE(X,train_y)) while diff > 1e-3: theta = theta - ETA * np.dot(f(X)-train_y,X) errors.append(MSE(X,train_y)) diff = errors[-2]-errors[-1] # 绘制误差变化图 x = np.arange(len(errors)) plt.plot(x,errors) plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
二、分类——感知机
训练数据集images1.csv如下:
x1,x2,y 153,432,-1 220,262,-1 118,214,-1 474,384,1 485,411,1 233,430,-1 396,361,1 484,349,1 429,259,1 286,220,1 399,433,-1 403,340,1 252,34,1 497,472,1 379,416,-1 76,163,-1 263,112,1 26,193,-1 61,473,-1 420,253,1- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
实现步骤:
1.首先要初始化感知机的权重,然后实现函数fw(x)。
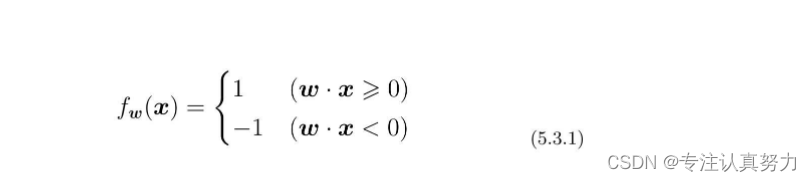
2.接下来只需实现权重的更新表达式。
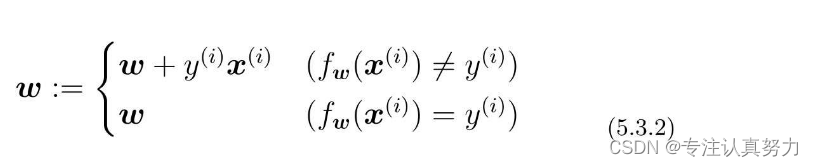
3.使权重向量成为法线向量的直线方程是内积为0的x的集合。所以对它进行移项变形,最终绘出以下表达式的图形即可。
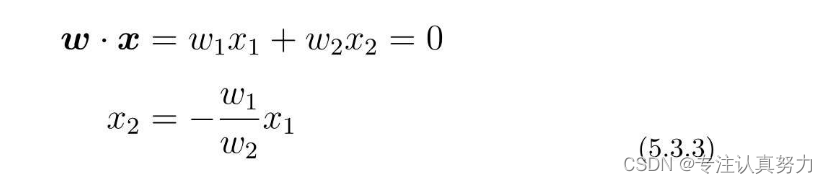
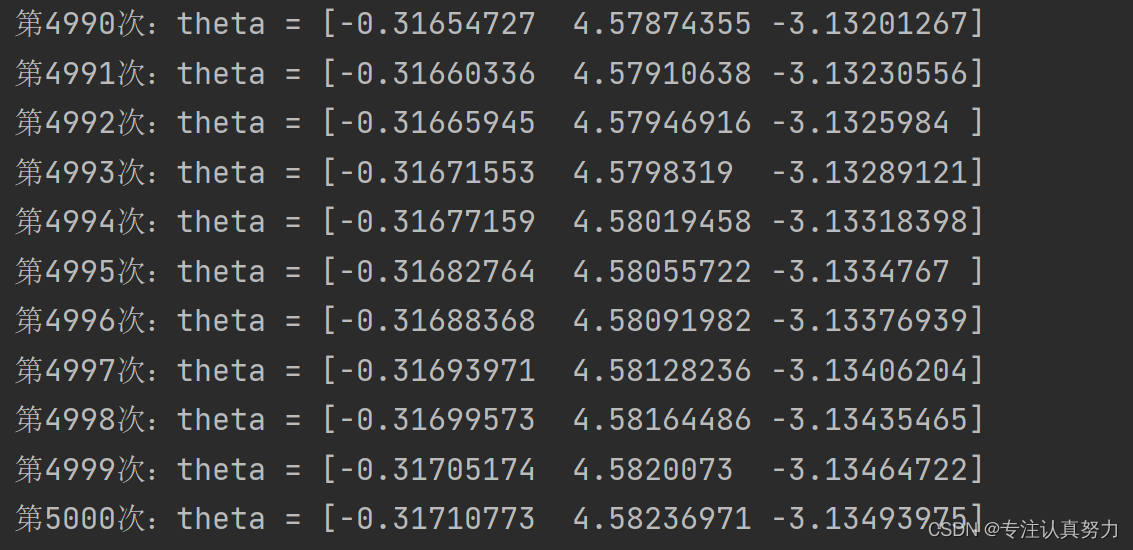
import numpy as np import matplotlib.pyplot as plt train = np.loadtxt("data/images1.csv", delimiter=",", skiprows=1) train_x = train[:, 0:2] train_y = train[:, 2] # 权重的初始化 w = np.random.rand(2) # 生成两个符合0-1分布的随机值,以列表形式保存 # 判别函数 def f(x_f): if np.dot(w, x_f) >= 0: return 1 else: return -1 # 重复次数 epoch = 10 # 更新次数 count = 0 # 学习权重 for _ in range(epoch): for x, y in zip(train_x, train_y): if f(x) != y: w = w + y * x # 输出日志 count += 1 print('第{}次:w={}'.format(count, w)) # 绘图 x1 = np.arange(0, 500) plt.title("classification_result") plt.xlabel('x1') plt.ylabel('x2') plt.plot(train_x[train_y == 1, 0], train_x[train_y == 1, 1], "o") plt.plot(train_x[train_y == -1, 0], train_x[train_y == -1, 1], "x") plt.plot(x1, -w[0] / w[1] * x1, linestyle='dashed') plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
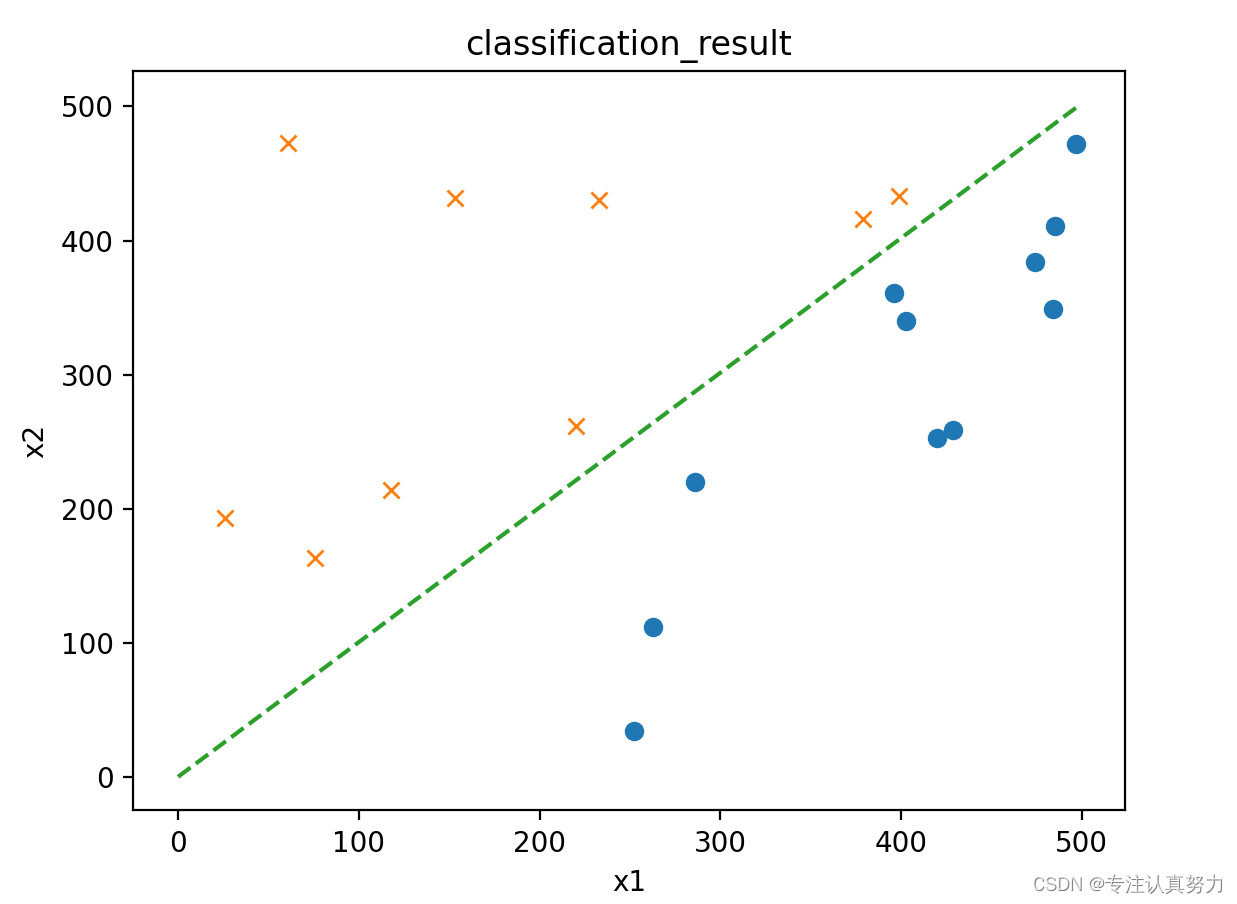
三、分类——逻辑回归
将images1.csv中的-1标签改变为0,得到训练数据集images2.csv如下:
x1,x2,y 153,432,0 220,262,0 118,214,0 474,384,1 485,411,1 233,430,0 396,361,1 484,349,1 429,259,1 286,220,1 399,433,0 403,340,1 252,34,1 497,472,1 379,416,0 76,163,0 263,112,1 26,193,0 61,473,0 420,253,1- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
实现步骤:
1.首先初始化参数,然后对训练数据标准化吧。x1和x2要分别标准化。另外不要忘了加一个x0列。
2.实现预测函数。
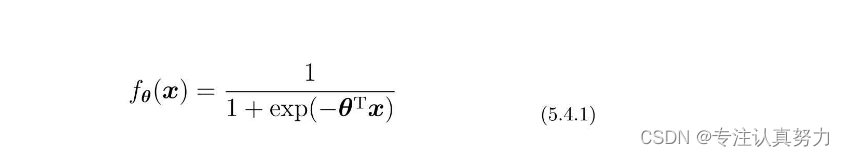
3.接下来是参数更新部分的实现。
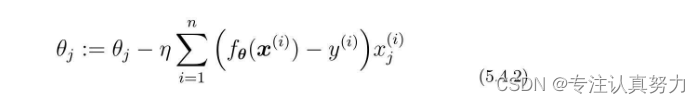
4. 将θTx=0变形并加以整理,得到这样的表达式。
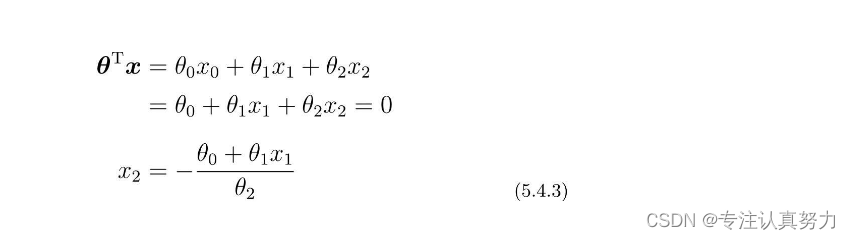
import numpy as np import matplotlib.pyplot as plt # 读入训练数据 train = np.loadtxt("data/images2.csv", delimiter=",", skiprows=1) train_x = train[:, 0:2] train_y = train[:, 2] # 参数初始化 theta = np.random.rand(3) # 标准化 mu = train_x.mean(axis=0) sigma = train_x.std(axis=0) def standardize(x): return (x - mu) / sigma train_z = standardize(train_x) # 增加x0 def to_matrix(x): x0 = np.ones([x.shape[0], 1]) return np.hstack([x0, x]) X = to_matrix(train_z) # sigmoid 函数 def f(x): return 1 / (1 + np.exp(-np.dot(x, theta))) # 分类函数 def classify(x): return (f(x) >= 0.5).astype(np.int) # 学习率 ETA = 1e-3 # 重复次数 epoch = 5000 # 更新次数 count = 0 # 重复学习 for _ in range(epoch): theta = theta - ETA * np.dot(f(X) - train_y, X) # 日志输出 count += 1 print('第{}次:theta = {}'.format(count, theta)) # 绘图确认 x0 = np.linspace(-2, 2, 100) plt.title("classification_result") plt.xlabel('x1') plt.ylabel('x2') plt.plot(train_z[train_y == 1, 0], train_z[train_y == 1, 1], 'o') plt.plot(train_z[train_y == 0, 0], train_z[train_y == 0, 1], 'x') plt.plot(x0, -(theta[0] + theta[1] * x0) / theta[2], linestyle='dashed') plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
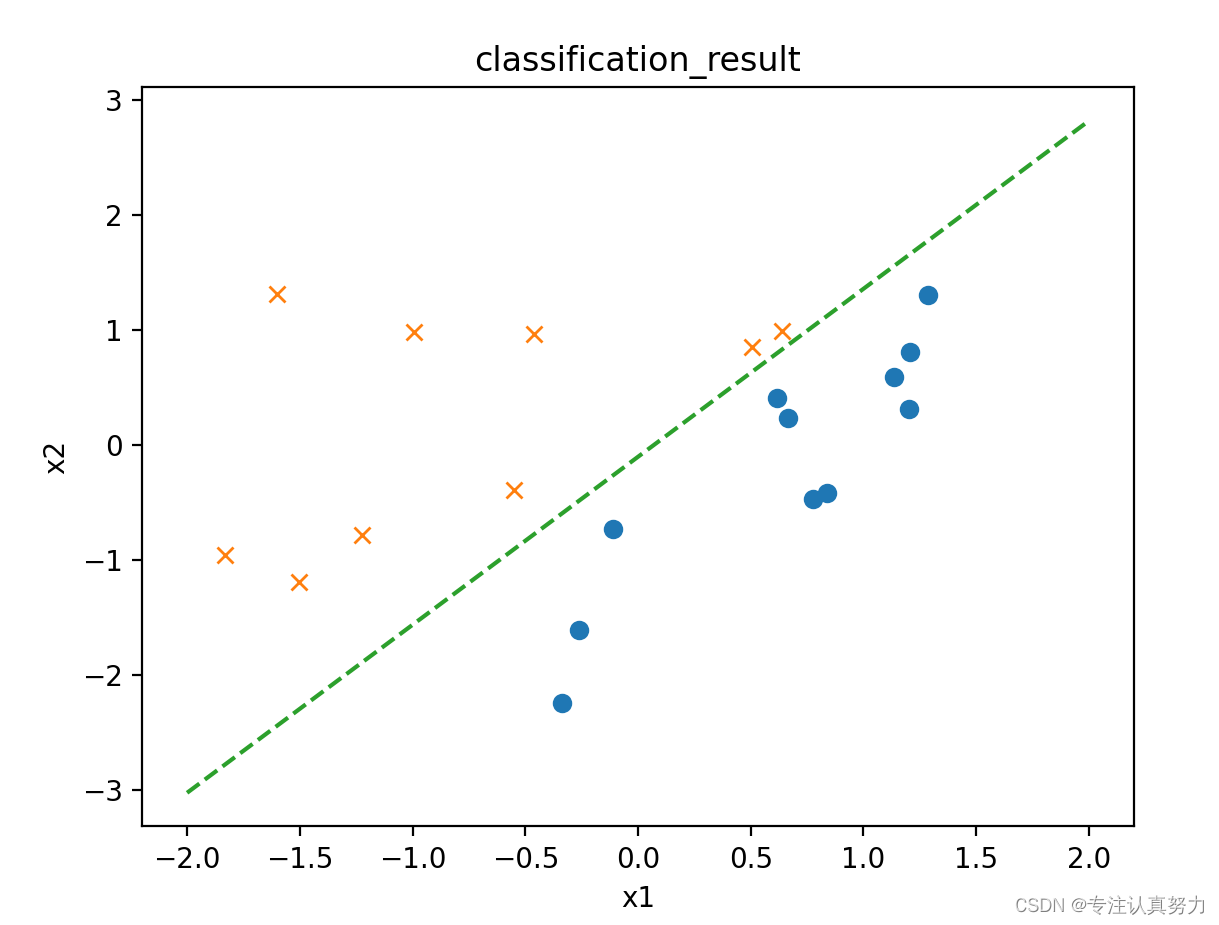
以上数据都可以通过一条直线将其进行分类,我们称之为线性可分的分类问题,对于如下数据,可以发现它们是无法仅仅通过一条直线就可以完成分类。
训练数据集data3.csv如下:x1,x2,y 0.54508775,2.34541183,0 0.32769134,13.43066561,0 4.42748117,14.74150395,0 2.98189041,-1.81818172,1 4.02286274,8.90695686,1 2.26722613,-6.61287392,1 -2.66447221,5.05453871,1 -1.03482441,-1.95643469,1 4.06331548,1.70892541,1 2.89053966,6.07174283,0 2.26929206,10.59789814,0 4.68096051,13.01153161,1 1.27884366,-9.83826738,1 -0.1485496,12.99605136 ,0 -0.65113893,10.59417745,0 3.69145079,3.25209182,1 -0.63429623,11.6135625,0 0.17589959,5.84139826,0 0.98204409,-9.41271559,1 -0.11094911,6.27900499,0- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
import numpy as np import matplotlib.pyplot as plt # 导入数据集 train = np.loadtxt("data/data3.csv", delimiter=",", skiprows=1) train_x = train[:, 0:2] train_y = train[:, 2] # 参数初始化 theta = np.random.rand(4) # 标准化 mu = train_x.mean(axis=0) sigma = train_x.std(axis=0) def standardize(x): return (x - mu) / sigma train_z = standardize(train_x) # 增加x0和x3 def to_matrix(x): x0 = np.ones([x.shape[0], 1]) x3 = x[:, 0, np.newaxis] ** 2 return np.hstack([x0, x, x3]) X = to_matrix(train_z) # sigmoid 函数 def f(x): return 1 / (1 + np.exp(-np.dot(x, theta))) # 分类函数 def classify(x): return (f(x) >= 0.5).astype(np.int) # 学习率 ETA = 1e-3 # 重复次数 epoch = 2000 # 更新次数 count = 0 # 精度的历史记录 accuracies = [] # 重复学习 for _ in range(epoch): theta = theta - ETA * np.dot(f(X) - train_y, X) # 日志输出 count += 1 print('第{}次:theta = {}'.format(count, theta)) # 计算现在的精度 result = classify(X) == train_y accuracy = len(result[result == True]) / len(result) accuracies.append(accuracy) x1 = np.linspace(-2, 2, 100) x2 = -(theta[0] + theta[1] * x1 + theta[3] * x1 ** 2) / theta[2] plt.title("classification_result") plt.xlabel('x1') plt.ylabel('x2') plt.plot(train_z[train_y == 0, 0], train_z[train_y == 0, 1], "o") plt.plot(train_z[train_y == 1, 0], train_z[train_y == 1, 1], "x") plt.plot(x1, x2, linestyle='dashed') plt.show() x = np.arange(len(accuracies)) plt.plot(x, accuracies) plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
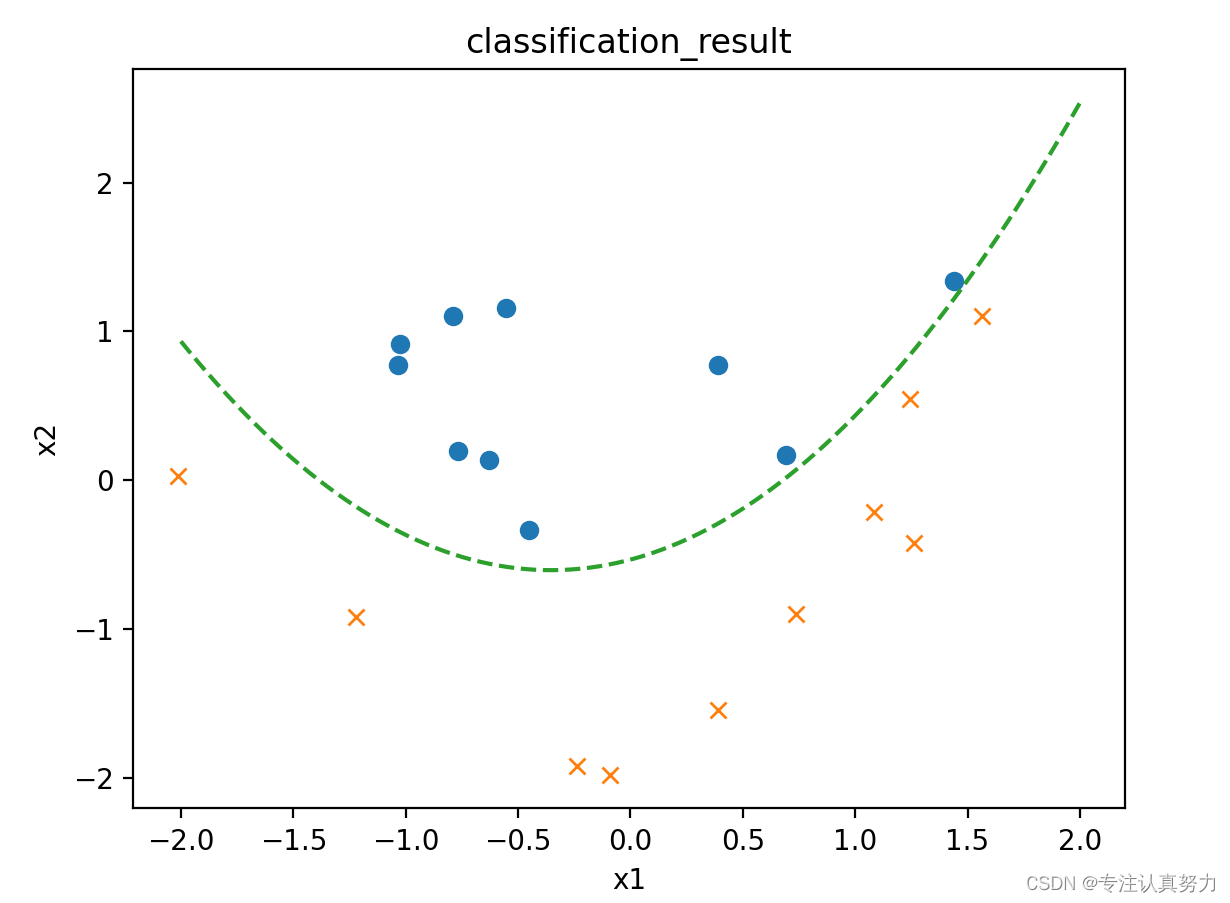
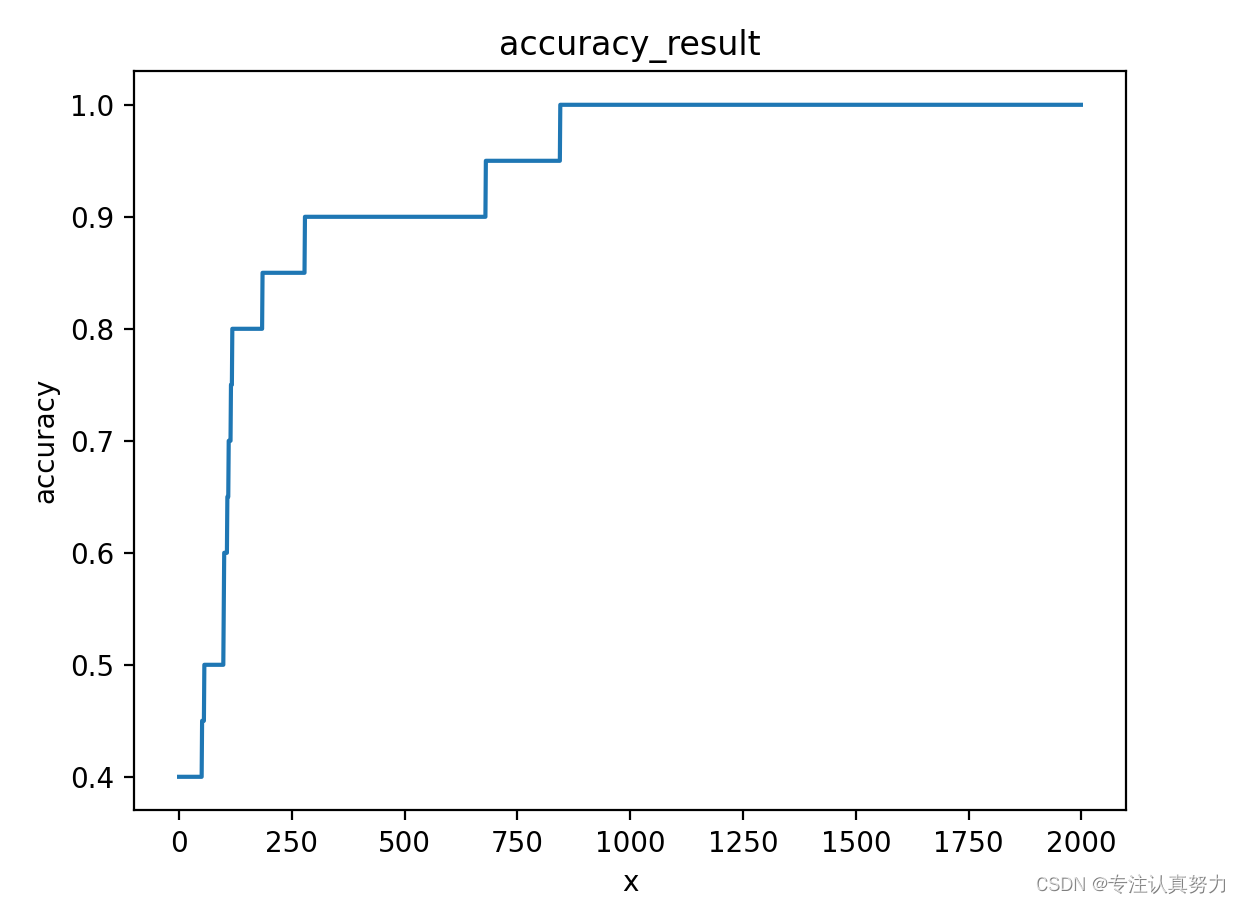
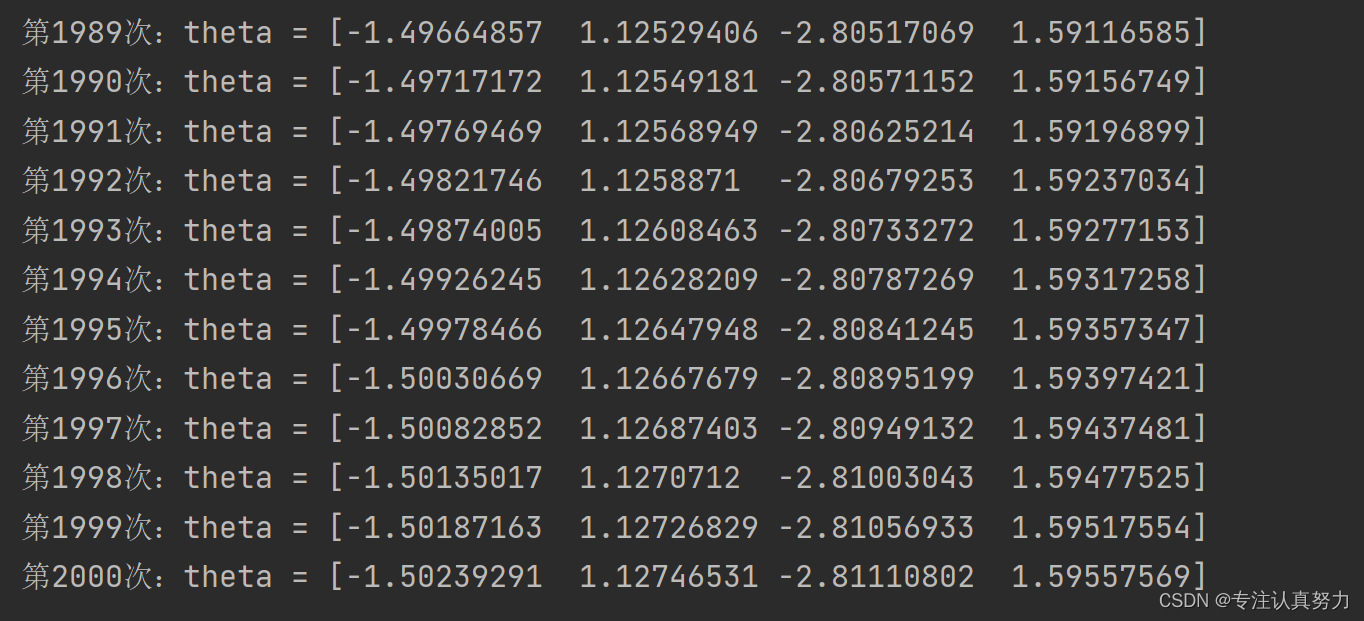
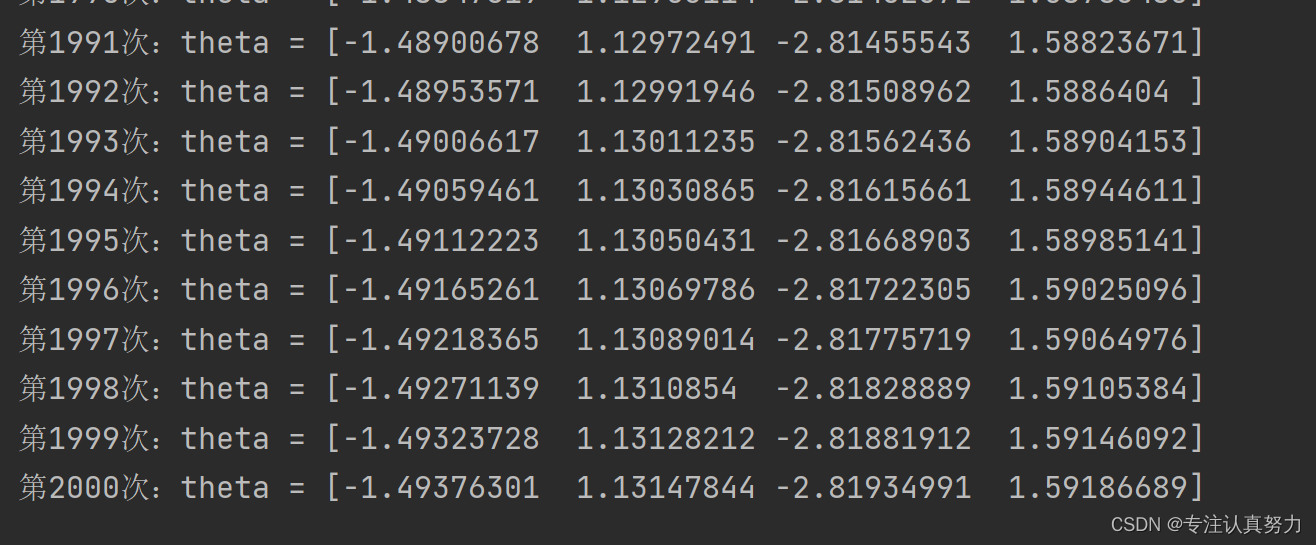
更新参数时,我们选择随机梯度下降的方法进行参数更新。import numpy as np import matplotlib.pyplot as plt # 导入数据集 train = np.loadtxt("data/data3.csv", delimiter=",", skiprows=1) train_x = train[:, 0:2] train_y = train[:, 2] # 参数初始化 theta = np.random.rand(4) # 标准化 mu = train_x.mean(axis=0) sigma = train_x.std(axis=0) def standardize(x): return (x - mu) / sigma train_z = standardize(train_x) # 增加x0和x3 def to_matrix(x): x0 = np.ones([x.shape[0], 1]) x3 = x[:, 0, np.newaxis] ** 2 return np.hstack([x0, x, x3]) X = to_matrix(train_z) # sigmoid 函数 def f(x): return 1 / (1 + np.exp(-np.dot(x, theta))) # 分类函数 def classify(x): return (f(x) >= 0.5).astype(np.int) # 学习率 ETA = 1e-3 # 重复次数 epoch = 2000 # 更新次数 count = 0 # 精度的历史记录 accuracies = [] # 重复学习 for _ in range(epoch): # 使用随机梯度下降法更新参数 p = np.random.permutation(X.shape[0]) for x, y in zip(X[p, :], train_y[p]): theta = theta - ETA * (f(x) - y) * x # 日志输出 count += 1 print('第{}次:theta = {}'.format(count, theta)) # 计算现在的精度 result = classify(X) == train_y accuracy = len(result[result == True]) / len(result) accuracies.append(accuracy) x1 = np.linspace(-2, 2, 100) x2 = -(theta[0] + theta[1] * x1 + theta[3] * x1 ** 2) / theta[2] plt.title("classification_result") plt.xlabel('x1') plt.ylabel('x2') plt.plot(train_z[train_y == 0, 0], train_z[train_y == 0, 1], "o") plt.plot(train_z[train_y == 1, 0], train_z[train_y == 1, 1], "x") plt.plot(x1, x2, linestyle='dashed') plt.show() x = np.arange(len(accuracies)) plt.title("accuracy_result") plt.xlabel('x') plt.ylabel('accuracy') plt.plot(x, accuracies) plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
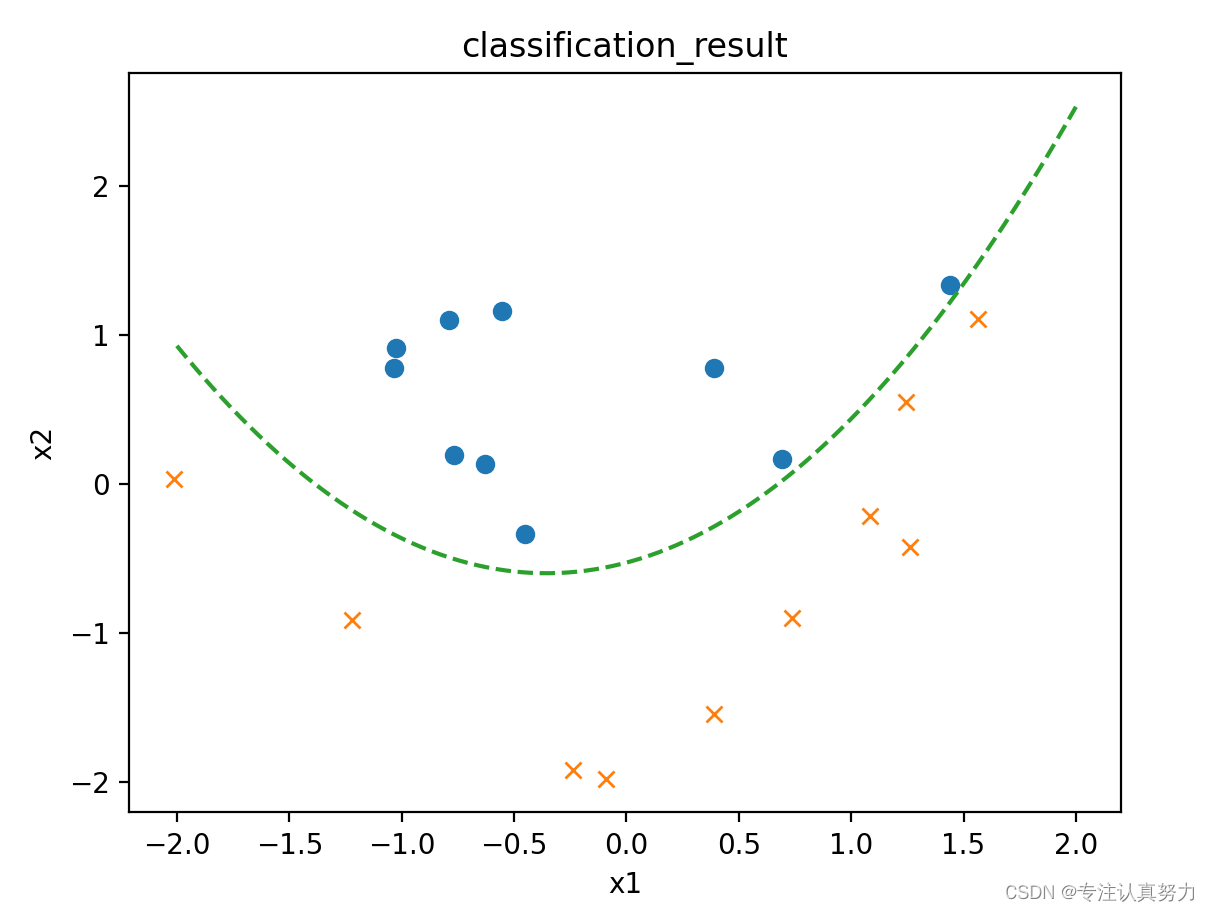
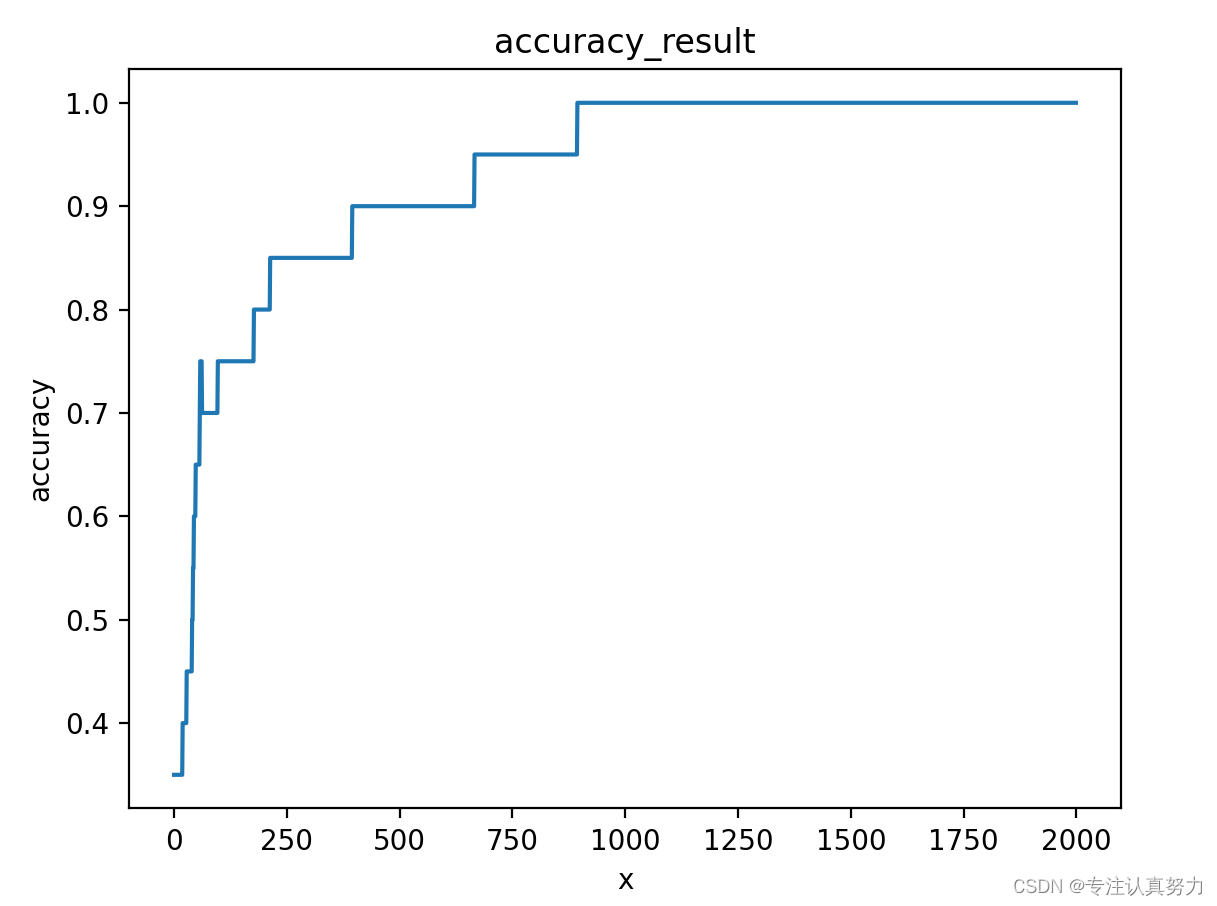
四、正则化
import numpy as np import matplotlib.pyplot as plt # 真正的函数 def g(x): return 0.1 * (x ** 3 + x ** 2 + x) # 随意准备一些向真正的函数加入了一点噪声的训练数据 train_x = np.linspace(-2, 2, 8) train_y = g(train_x) + np.random.rand(train_x.size) * 0.05 # 绘图确认 plt.plot(train_x, train_y, 'o') x = np.linspace(-2, 2, 100) plt.plot(x, g(x), linestyle="dashed") plt.ylim(-1, 2) plt.show() # 标准化 mu = train_x.mean() sigma = train_x.std() def standardize(x): return (x - mu) / sigma train_z = standardize(train_x) # 创建训练数据的矩阵 def to_matrix(x): return np.vstack([np.ones(x.size), x, x ** 2, x ** 3, x ** 4, x ** 5, x ** 6, x ** 7, x ** 8, x ** 9, x ** 10]).T X = to_matrix(train_z) # 参数初始化 theta = np.random.randn(X.shape[1]) # 预测函数 def f(x): return np.dot(x, theta) # 目标函数 def E(x, y): return 0.5 * np.sum((y - f(x)) ** 2) # 学习率 ETA = 1e-4 # 误差 diff = 1 # 重复学习 error = E(X, train_y) while diff > 1e-6: theta = theta - ETA * np.dot(f(X) - train_y, X) current_error = E(X, train_y) diff = error - current_error error = current_error # 对结果绘图 z = standardize(x) plt.plot(train_z, train_y, 'o') plt.plot(z, f(to_matrix(z))) plt.show() # 保存未正则化的参数,然后再次参数初始化 theta1 = theta theta = np.random.randn(X.shape[1]) # 正则化常量 LAMBDA = 1 # 误差 diff = 1 # 重复学习(包含正则化项) error = E(X, train_y) while diff > 1e-6: # 正则化项。偏置项不适合正则化,所以为0 reg_term = LAMBDA * np.hstack([0, theta[1:]]) # 应用正则化项,更新参数 theta = theta - ETA * (np.dot(f(X) - train_y, X) + reg_term) current_error = E(X, train_y) diff = error - current_error error = current_error # 对结果绘图 plt.plot(train_z, train_y, 'o') plt.plot(z, f(to_matrix(z))) plt.show() theta2 = theta plt.plot(train_z, train_y, 'o') # 画出未正则化的结果 theta = theta1 plt.plot(z, f(to_matrix(z)), linestyle='dashed', label="non_regularization") # 画出正则化的结果 theta = theta2 plt.plot(z, f(to_matrix(z)), label="regularization") plt.legend() plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
我们利用一个真正的函数来生成数据,并在其中添加随机的噪声,以对现实进行模拟。
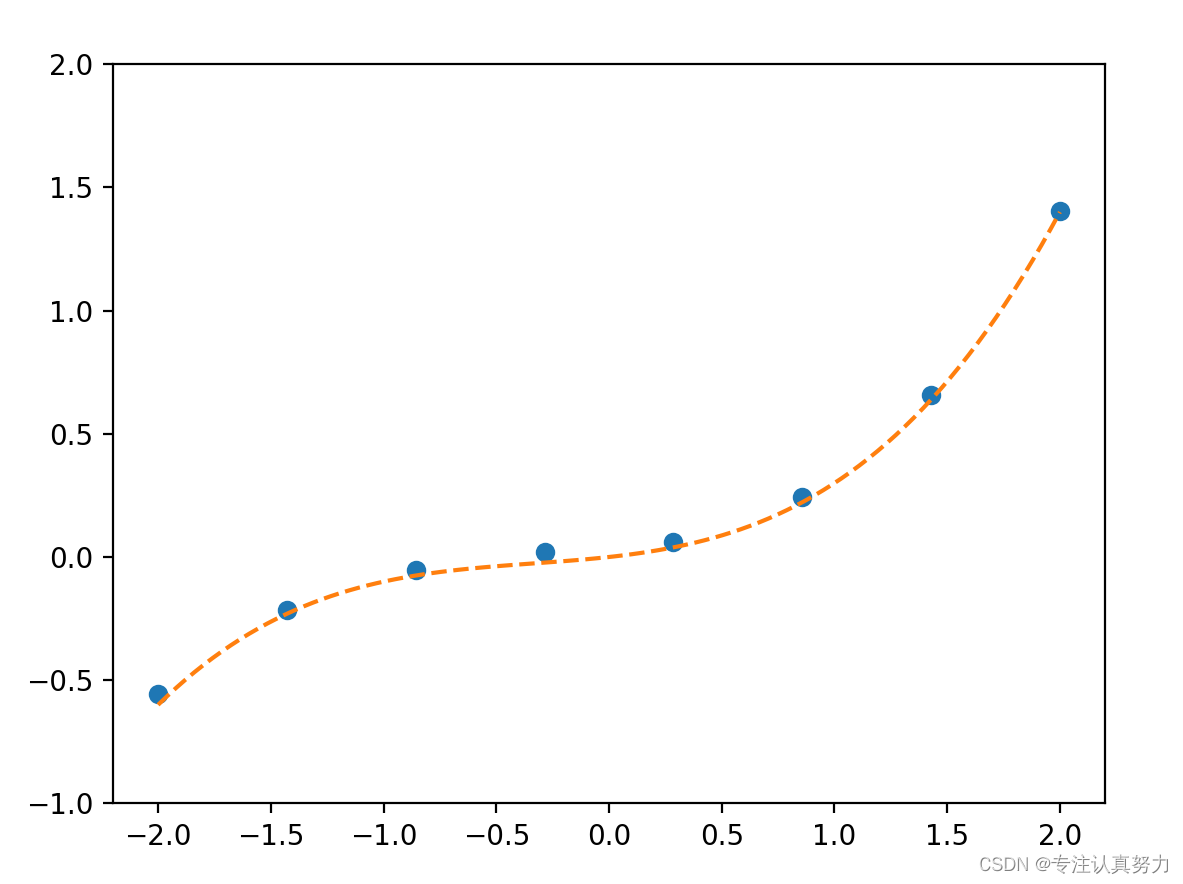
不进行正则化处理的学习效果。
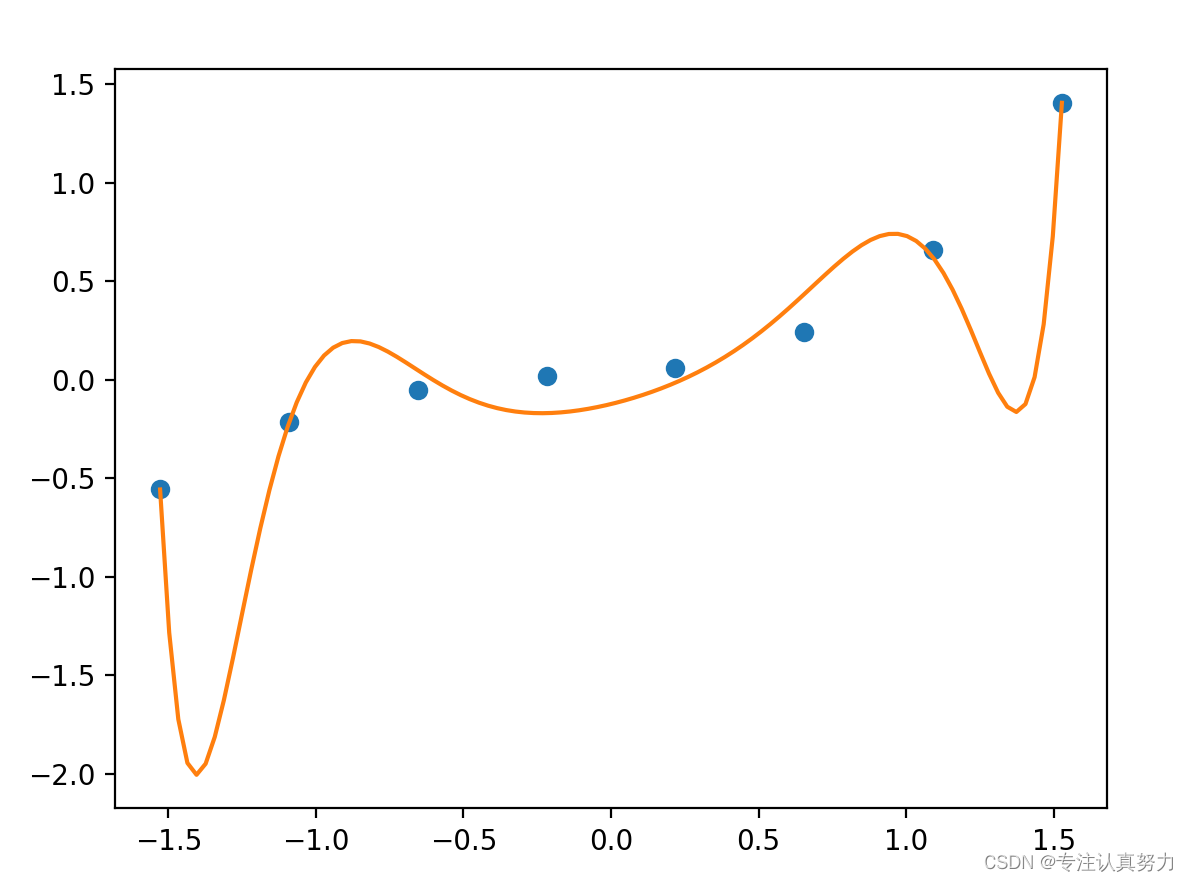
进行正则化处理的学习结果。
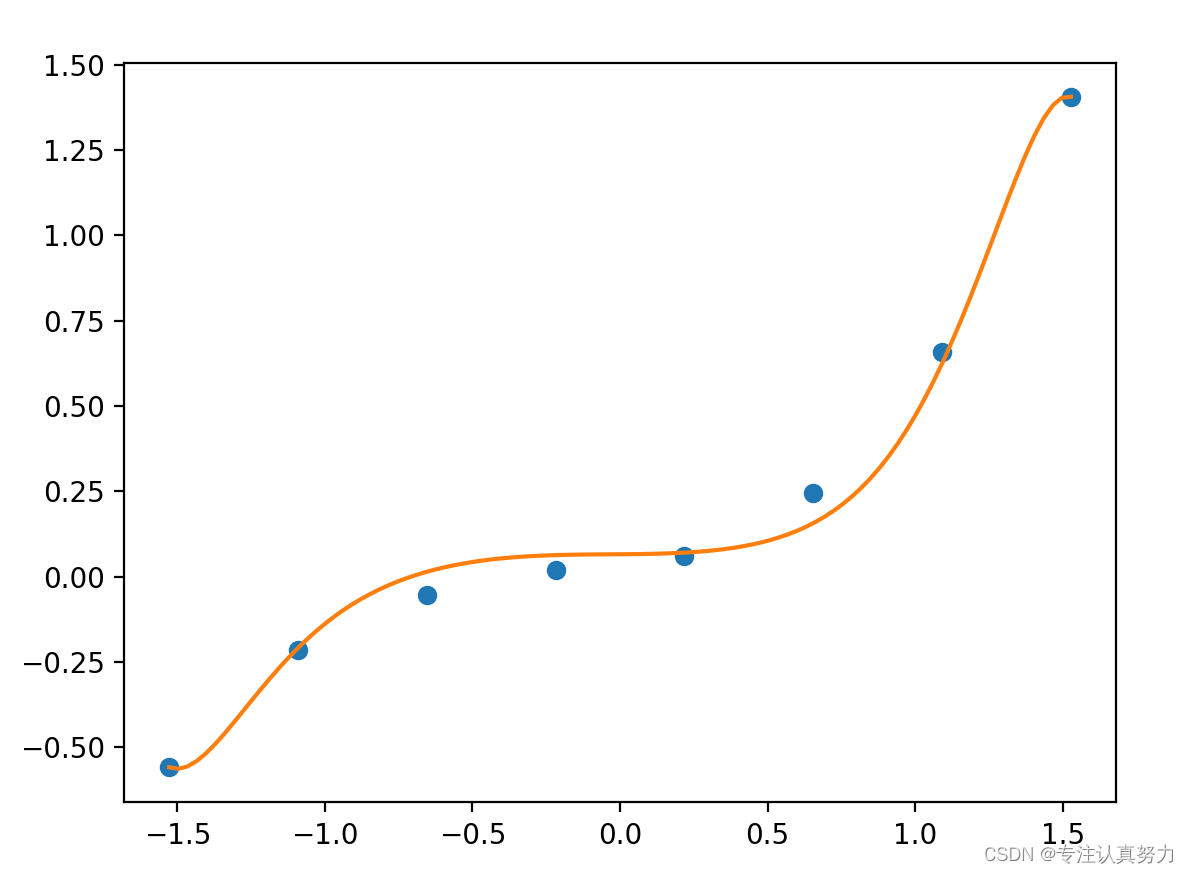
两者间的对比。
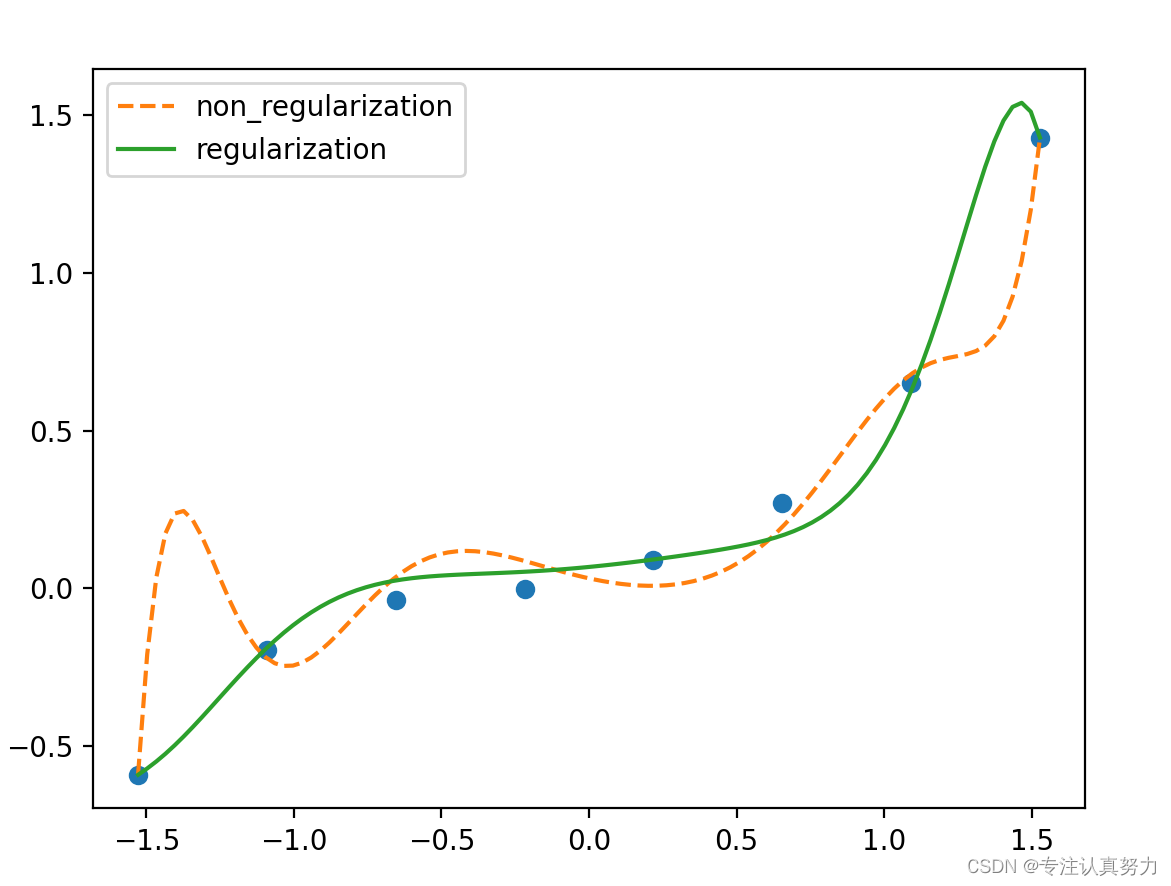
-
相关阅读:
HTML定位相关
Google guava之BiMap简介说明
Python-类
6、Linux驱动开发:设备-更简单的设备注册
Mybatis 一级缓存和二级缓存原理区别 (图文详解)
Effctive C++
【德哥说库系列】-PostgreSQL跨版本升级
Explaining Deepfake Detection by Analysing Image Matching 翻译
基于android的宠物领养系统
贪心算法学习——单调递增的数字
- 原文地址:https://blog.csdn.net/m0_46692607/article/details/127536337
