关于如何计算 递归 方法 的时间复杂度 笔记总结

经典的几个递归关系 和 它们的时间复杂度

第一个 T（n） = T(n /2 ) + O(1)
每次 n 缩小 一半，所以 一共会执行 log2 n 次
每次的时间复杂度 为 O(1)
总的时间复杂度 为 log2n * O(1) = log2n
所以 时间复杂度 为 O(logn)

第二个
每次 n 只减少 1 次，所以 一共执行 n次
每次时间复杂度为 O(1)
总的时间复杂度为 n * O(1) = O(n)

第三个
T(N) = 2T(N/ 2) + O(1)
每次 2 的 n次方 个减少一半 表示为 2的n次方 ，n 是 log2 n
所以总过执行 2 ^ log2 n 次
每次 时间复杂度 为 O(1)
总的时间复杂度 为 2 ^ log2 n * O(1)
时间复杂度 为 O(n)

第四个
T(N) = 2 T(N / 2) + O(N)
每次 2 的 n次方 个减少一半 表示为 2的n次方 ，n 是 log2 n
所以总过执行 2 ^ log2 n 次
即 n次

每次 时间复杂度为 O(n)
总的时间复杂度就为 O (nlogn)

第五个
T(N) = 2 T(N / 2) + O(NlogN)
时间复杂度 为 n(logn)^2
这个我不太懂

第六个
T（n） = T(N - 1) + O(N)
n次
单次 O(N)
总共 O(N ^ 2)

第七个
T(N) = 2 T(N - 1) + O(1) 汉诺塔
时间复杂度 为 2的n次

第八个
最后一个斐波那契
我认为 将两个T合并
所以 可以看做 2 * T(n-1) 或 2 * T(n -2)
这样的话，总共会执行 2的 n次
单次 时间复杂度 为O(1)
总的时间复杂度 就为 2 的n次方

Master公式

N 表示问题的规模
a 表示一次递推的子问题的数量
\frac{N}{b} 表示每个子问题的规模，每个子问题的规模要一样（这里的一样不是绝对的一样，比如把问题规模N除以2，分成两个子问题，这就是一样）
O(N^d) 表示递归以外进行的计算的时间复杂度
1
2
3
4

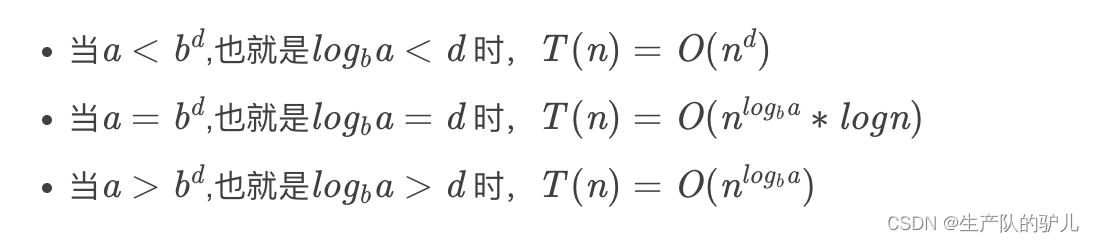
常见 时间复杂度 面试问题

二叉树 的遍历 前中后 序 时间复杂度

O(N)
这里的n代表二叉树里边树的节点的总数，不管是哪种方式遍历，每个节点都有且仅访问一次，所以它的复杂度是线性于二叉树的节点总数，也就是O(n)

图 的遍历 时间复杂度
O(N)
图中的每一个节点也是有且仅访问一次，因此时间复杂度也是O(n)，n为图中的节点总数

DFS 和 BFS的时间复杂度
O(N)

二分查找
O(logn)

Reference

https://www.zhihu.com/question/63075755
https://juejin.cn/post/6854573216908705806
https://blog.csdn.net/jmh1996/article/details/82827579?utm_medium=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase