C语言题解 | 消失的数字&轮转数组

…

🌳🌲🌱本文已收录至：C语言题解系列
更多知识尽在此专栏中！

🎉🎉🎉欢迎点赞、收藏、关注 🎉🎉🎉

🍉前言

在 数据结构 | 时间复杂度与空间复杂度 一文中，分享了两个和复杂度相关的例题，现在就来给大家分享下这两个题的多种解法

题目链接

1. 消失的数字
2. 轮转数组

---

🍉正文

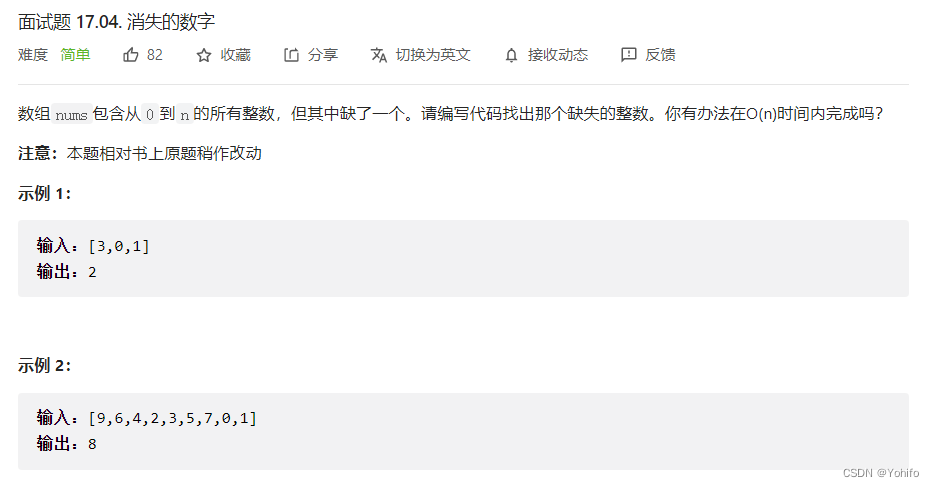
🍍题目一、消失的数字

🍌先看题目

---

🍌分析

题目的意思就是存在一个数组 nums ，数组中元素范围为 0 ~ N ，其中缺少了一个元素，因为本来只能放下元素 1 ~ N 的，但是 0 把某个数字给顶替掉了，这样好理解下，就像办案一样，我们要找出那个消失的目标

解题关键：

• 数组内的元素仅会出现一次，并且元素范围为 0 ~ N

我们可以从这个关键点出发，得出多种思路

---

🍌解题思路

🍎思路一

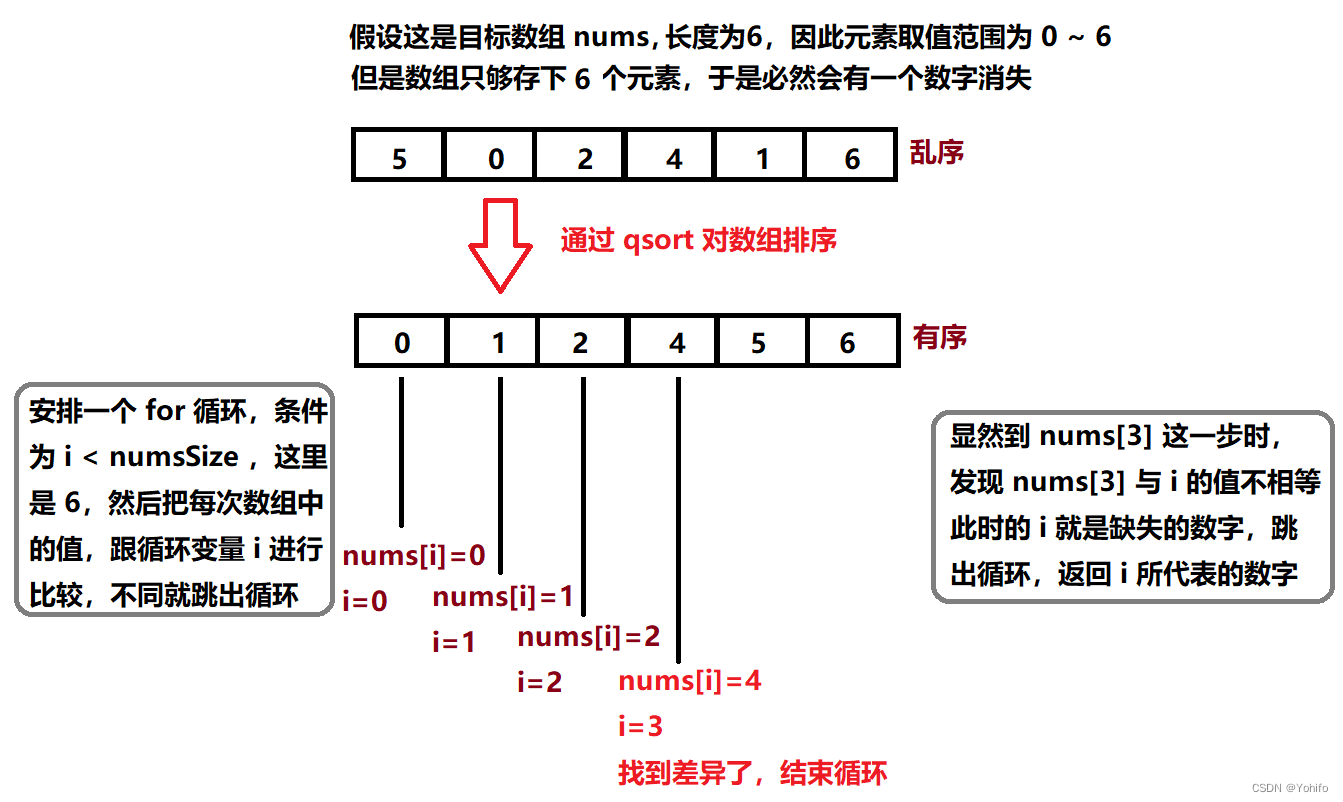
暴力解决 ，这个东西依赖于数组有序，于是我们可以先使用 qsort 把数组变为有序(关于 qsort 的使用)，排好序后，对这个数组进行 遍历 ，可以把元素值和循环变量 i 进行比较，如果发现不相等 ，那么此时的 i 就是缺失的数字，查找成功，返回数字

问题貌似解决了，但题目有个要求，时间复杂度要控制在 O(N) 内
用所学的知识分析一波

• qsort 的 时间复杂度 是 O(logN*N)
遍历，按最坏的情况判断，时间复杂度 是 O(N)
  两个时间一加，显然不符合题目要求，这个方案Pass掉
  代码实现很简单，但它不够完美，如果题目没限制的话，这个算法是能解决问题的，力扣上能通过，但 不推荐使用 ，知道解题思想就行了

//思路一
//暴力解决
#include
//qsort 中的比较函数
int cmp(void* e1, void* e2)
{
	return *(int*)e1 - *(int*)e2;	//需要强转为整型
}
int missingNumber(int* nums, int numsSize) {
	qsort(nums, numsSize, sizeof(int), cmp);	//先排序
	int i = 0;
	//注意：条件是 i < numsSize,如果写成 i <= numsSize 数组会越界的
	for (i = 0; i < numsSize; i++)
	{
		if (i != nums[i])
			break;
	}
	//如果循环不是终止，而是正常结束的，说明在整个数组中都没有找到目标
	//即目标是 N ，此时也不用担心，循环正常结束后，i 还会加一次
	//不管怎么说，i 都是目标数
	return i;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

---

🍎思路二

相加相减 ，这个算法比较巧妙，用到了差异的特别之处，举个例子，有数字 1、3 ，其中缺少了数字 2 ，相加后为 4 ，我们将数字 1、2、3 相加得到 6 ，6 - 4 得到的就是缺少的数字 2 了。这个算法是很巧妙的，只需要遍历两次，然后相减，就能得到结果了。

这个算法巧妙在哪呢？

• 几乎没有创建额外空间
• 两次 for 循环解决问题
• 通俗易懂

照样分析一波 时间复杂度 :

• 首先 遍历 数组，所耗时间为 N
• 其次 for 循环，所耗时间为 N+1
• 两者相加，通过大O渐进法，最终时间复杂度为 O(N)，空间复杂度为 O(1)

达到这种复杂度的算法，都属于比较优秀的算法~
下面是代码实现

//思路二
//相加相减
int missingNumber(int* nums, int numsSize) {
	int tmp = 0;	//临时存储数组和值
	int i = 0;
	for (i = 0; i < numsSize; i++)
		tmp += nums[i];
	int sum = 0;	//存储理想状态下的和值
	for (i = 0; i <= numsSize; i++)
		sum += i;

	return sum - tmp;	//直接返回二者的差值
}
1
2
3
4
5
6
7
8
9
10
11
12
13

---

🍎思路三

异或求值，怎么说呢，这个东西属于奇技淫巧了，因为用到了位运算，众所周知，涉及位运算的算法都是比较厉害的，恰巧这题就能用。原理跟 思路二 差不多，比如有数字 1、3 ，二者异或后，会得到 2 这个数；在把理想数字 1、2、3 ，三者异或后，得到 0，将异或数 2 和异或数 0 再异或一次，得到消失的数字 2，用到了异或运算符的特点，可以点击这里回顾下用法

这个算法很厉害的，因为位运算对于计算机来说就是小菜一碟，如同探囊取物一般很快就计算出来了
分析时间复杂度：

• 第一次 for 循环 N
• 第二次 for 循环 N+1
• 两者相加，通过 大O渐进表示法 ，最终结果为 时间复杂度 O(N) 空间复杂度 O(1)

虽然思路二三复杂度一致，得益于位运算，思路三比思路二更快！
下面是代码表示

//思路三
//异或求值
int missingNumber(int* nums, int numsSize) {
	int tmp = 0;	//临时存储数组元素异或值
	int i = 0;
	for (i = 0; i < numsSize; i++)
		tmp ^= nums[i];	//逐元素异或

	int sum = 0;	//存储理想状态下的异或值
	for (i = 0; i <= numsSize; i++)
		sum ^= i;	//也是逐元素异或

	return tmp ^ sum;	//返回二者的异或结果
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

题目一完美收官了，让我们来接着看题目二！

---

🍍题目二、轮转数组

🍌再看题目

---

🍌分析

这是一个中等题，是一个不太难的中等题。题目的意思是存在一个数组 nums ，里面有 numsSize 个元素，现在有一个位置变量 k 表示需要轮转的次数，这里的轮转是左轮转。假设数组内元素为 1、2、3 ，k 为 1，那么经过轮转后，数组会变为 3、1、2，显然轮转 numsSize * n 次后，就变成了最初的样子，因此在设计程序时，要先加上 k %= numsSize 这句话，去除多余的轮转操作。

解题关键

• 这是一个数组，轮转超过最大长度后，会变回原样
• 可以使用三步翻转法

来看看解题思路吧！

---

🍌解题思路

三步翻转法，其实轮转数组类似于之前介绍过的倒置字符串，即整体先翻转，左半部分翻转，右半部分翻转，就能得到最终结果。假设数组 nums 为 1、2、3、4、5，轮转 3 次，先整体翻转(0 ~ numsSize - 1)，数组为 5、4、3、2、1，再翻转左半部分(0 ~ k - 1)，数组为 3、4、5、2、1，最后再翻转右半部分(k ~ numsSize - 1)，数组为 3、4、5、1、2，结果出来了，这就是 三步翻转法 的奇妙解法

三步翻转法 太妙了

• 只需调用三次翻转函数
• 没有额外开辟空间

复杂度分析：

• 三次调用，第一次交换了 N / 2 次，第二次 + 第三次交换了 N / 2 次，总共耗时 N
• 因此时间复杂度为 O(N) 空间复杂度为 O(1)

理解翻转函数的设计和函数传参时的边界，代码就很好写了

//三步翻转
//翻转函数，通过下标操作
void rever(int* nums, int left, int right) 
{
	while (left < right)
	{
		//交换需要借助第三个变量
		int tmp = nums[left];
		nums[left] = nums[right];
		nums[right] = tmp;
		left++;
		right--;
	}
}
void rotate(int* nums, int numsSize, int k) {
    k %= numsSize;  //去除多余的轮转次数
	rever(nums, 0, numsSize - 1);	//第一次翻转
	rever(nums, 0, k - 1);	//第二次翻转
	rever(nums, k, numsSize - 1);	//第三次翻转
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

这题还有很多解法，限于篇幅原因，无法一一列举，因此这里只是指出了比较优秀的解法分享给大家，三步翻转法 完美符合题目要求，是一个好算法

---

🍉总结

以上就是本篇题解系列的所有内容了，分享了几种奇妙解法给大家，同时运用了之前学的知识，分析了 时间复杂度 与 空间复杂度 ，在多种算法中选出较优解法，这是比较有意义的。

如果你觉得本文写的还不错的话，期待留下一个小小的赞👍，你的支持是我分享的最大动力！

如果本文有不足或错误的地方，随时欢迎指出，我会在第一时间改正

…

相关文章推荐
数字在升序数组中出现的次数
除自身以外数组的乘积
倒置字符串