语法分析树
：
2
型文法
的
句型
推导的图形表示，简称
语法树
语法树表示了一个
句型
种种
可能的
不
同
推导过程
。
最左推导
:任
何一步
α →
β
都是对
α
的最左非终结符进
行替换的。
—与
最右归约对应
E ⇒
lm
(
E) ⇒
lm
(
E
+
E)⇒
lm
(i +
E)⇒
lm (i + i)
最右推导（规范推导）
—与
最左归约（规范规
约）相对应
E ⇒
rm(
E) ⇒
rm (
E
+
E)⇒
rm
(
E + i)⇒
rm (i + i)
文法的二义性
：若一个文法存在
某个句子
对应
两棵不同的语
法树
，则称此文法是二义性文法。
例子：
句型分析
就是识别一个
符号串
是否为某文法的
句型
，
是某个推导的构造过程
句型分析算法分为两类
自顶向下的分析方法
思想
：对一个输入串，从文法
开始符号
（根
结点）出发，采用一切可能的办法
(
复用各种
规则进行推导
)
，从上（根结点）而下的为输
入串建立一棵语法树。
核心问题
：在推导过程中
如何选择规则
自底向上的分析方法
思想
：对一个输入串，逐步进行“规约”，
试图规约到文法的开始符号。
核心问题
：在规约过程中
如何选择可规约串
短语、直接短语、句柄
短语：
已知文法
G
，文法开始符号
S,
设
αβδ
是文法
G
的
一个句型
,
若S ⇒
*
αAδ且A⇒
+
β
则称
β
是句型
αβδ
的相对于非终结符
A
的短语。
直接短语：
若有 S ⇒
*
αAδ且
A ⇒
β
，
称
β
是句型
αβδ
的相对于规则
A→
β
的直接短语。
句柄：
一个句型的
最左直接短语
称为该句型的句柄
有害规则
应限制文法中不得含有有害规则
U→
U 自己指向自己这种的规则就是有害规则
多余规则
应限制文法中不得含有多余规则即不
可到达 不
可终止
最左推导 :任 何一步 α → β 都是对 α 的最左非终结符进 行替换的。 —与 最右归约对应E ⇒ lm ( E) ⇒ lm ( E + E)⇒ lm (i + E)⇒ lm (i + i)最右推导（规范推导） —与 最左归约（规范规 约）相对应E ⇒ rm( E) ⇒ rm ( E + E)⇒ rm ( E + i)⇒ rm (i + i)文法的二义性 ：若一个文法存在 某个句子 对应 两棵不同的语 法树 ，则称此文法是二义性文法。例子：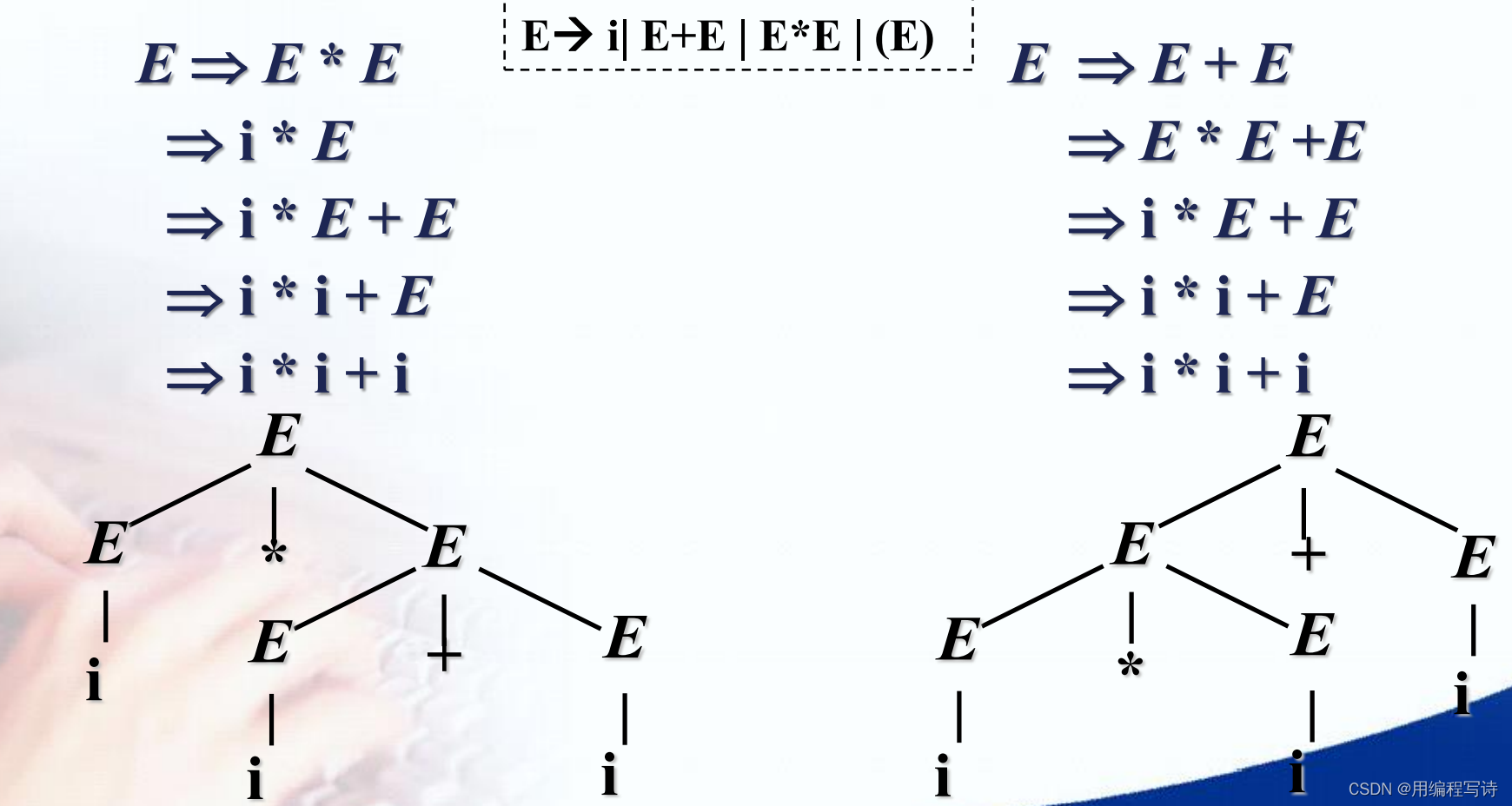
句型分析就是识别一个 符号串 是否为某文法的 句型 ， 是某个推导的构造过程句型分析算法分为两类自顶向下的分析方法思想 ：对一个输入串，从文法 开始符号 （根 结点）出发，采用一切可能的办法 ( 复用各种规则进行推导 ) ，从上（根结点）而下的为输 入串建立一棵语法树。核心问题 ：在推导过程中 如何选择规则自底向上的分析方法思想 ：对一个输入串，逐步进行“规约”， 试图规约到文法的开始符号。核心问题 ：在规约过程中 如何选择可规约串短语、直接短语、句柄短语： 已知文法 G ，文法开始符号 S, 设 αβδ 是文法 G 的 一个句型 , 若S ⇒ * αAδ且A⇒ + β 则称 β 是句型 αβδ 的相对于非终结符 A 的短语。直接短语： 若有 S ⇒ * αAδ且 A ⇒ β ， 称 β 是句型 αβδ 的相对于规则 A→ β 的直接短语。句柄： 一个句型的 最左直接短语 称为该句型的句柄有害规则 应限制文法中不得含有有害规则 U→ U 自己指向自己这种的规则就是有害规则多余规则 应限制文法中不得含有多余规则即不 可到达 不 可终止