-
【深度学习】深度学习中模型计算量(FLOPs)和参数量(Params)等的理解以及四种在python应用的计算方法总结
接下来要分别概述以下内容：
１ 首先什么是参数量，什么是计算量
２ 如何计算 参数量，如何统计 计算量
３ 换算参数量，把他换算成我们常用的单位，比如:mb
４ 对于各个经典网络，论述他们是计算量大还是参数量，有什么好处
５ 计算量，参数量分别对显存，芯片提出什么要求，我们又是怎么权衡
深度学习中模型参数量和计算量的理解与计算
1 首先什么是计算量，什么是参数量
计算量对应我们之前的时间复杂度，参数量对应于我们之前的空间复杂度，这么说就很明显了
也就是计算量要看网络执行时间的长短，参数量要看占用显存的量
其中最重要的衡量CNN 模型所需的计算力就是flops：
- FLOPS： 注意全大写，是floating point operations per second的缩写，意指每秒浮点运算次数，理解为计算速度。是一个衡量硬件性能的指标。
- FLOPs： 注意s小写，是floating point operations的缩写（s表复数），意指浮点运算数，理解为计算量。可以用来衡量算法/模型的复杂度。
我们知道，通常我们去评价一个模型时，首先看的应该是它的精确度，当你精确度不行的时候，你和别人说我的模型预测的多么多么的快，部署的时候占的内存多么多么的小，都是白搭。但当你模型达到一定的精确度之后，就需要更进一步的评价指标来评价你模型：1）前向传播时所需的计算力，它反应了对硬件如GPU性能要求的高低；2）参数个数，它反应所占内存大小。为什么要加上这两个指标呢？因为这事关你模型算法的落地。比如你要在手机和汽车上部署深度学习模型，对模型大小和计算力就有严格要求。模型参数想必大家都知道是什么怎么算了，而前向传播时所需的计算力可能还会带有一点点疑问。所以这里总计一下前向传播时所需的计算力
2 如何计算：参数量，计算量
（１）针对于卷积层的
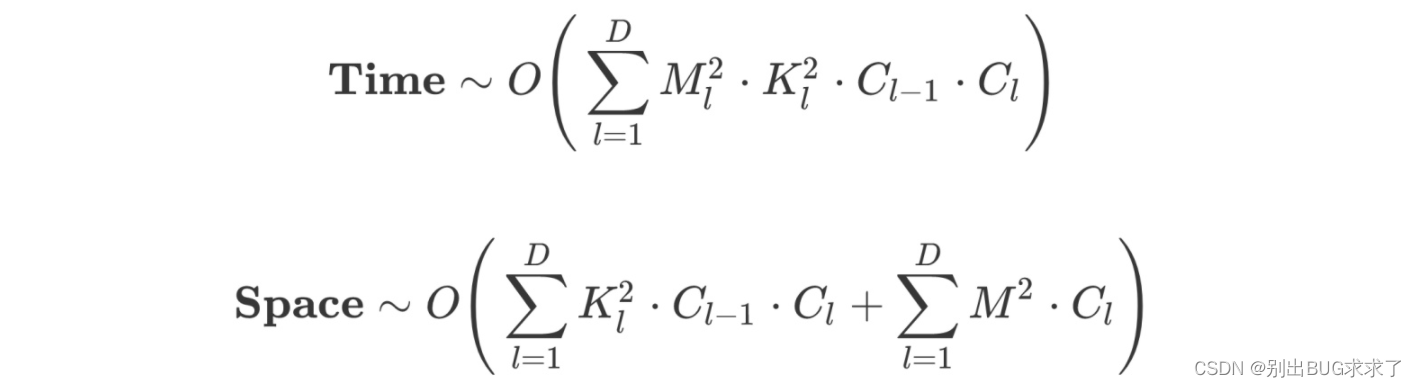
其中上面的公式是计算时间复杂度(计算量)，而下面的公式是计算空间复杂度(参数量)对于卷积层：
（a）参数量就是
(kernel*kernel) *channel_input*channel_output kernel*kernel 就是 weight * weight 其中kernel*kernel ＝ 1个feature的参数量- 1
- 2
- 3
- 4
- 5
（b）计算量就是
(kernel*kernel*map*map) *channel_input*channel_output kernel*kernel 就是weight*weight map*map是下个featuremap的大小，也就是上个weight*weight到底做了多少次运算 其中kernel*kernel*map*map＝ 1个feature的计算量- 1
- 2
- 3
- 4
- 5
- 6
- 7
详细解释：
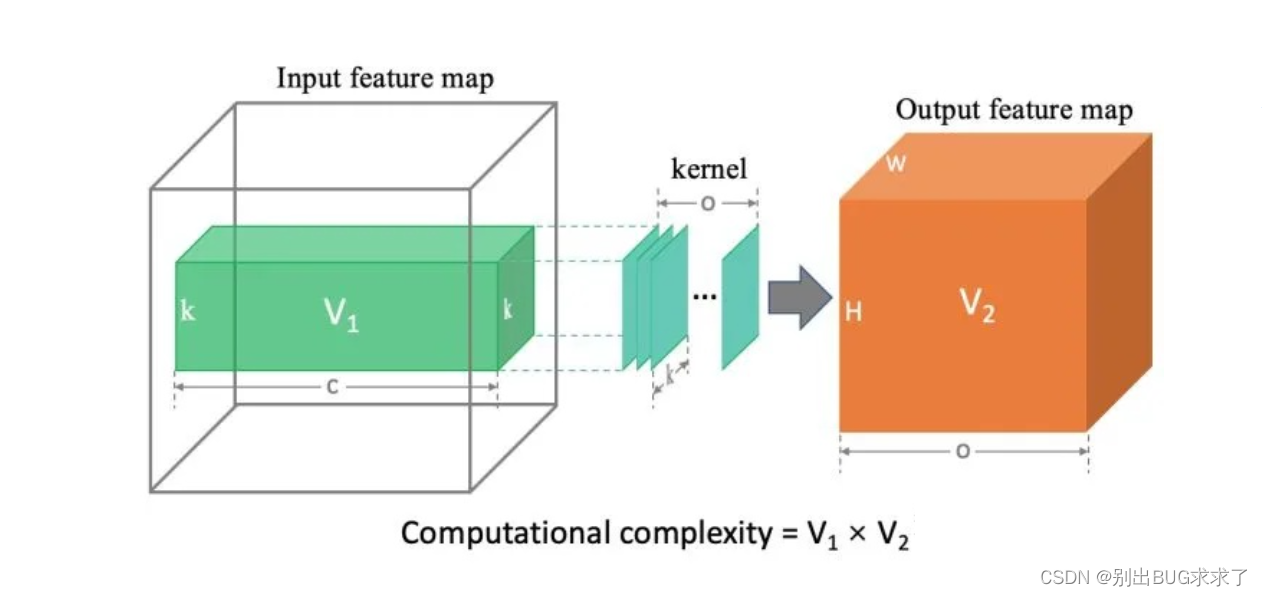
先说结论：卷积层 计算力消耗 等于上图中两个立方体 (绿色和橙色) 体积的乘积。即flops =**推导过程：**卷积层 wx + b 需要计算两部分，首先考虑前半部分 wx 的计算量：
令 :
- k 表示卷积核大小;
- c 表示输入 feature map 的数量;
- 则对于输出 feature map 上的单个 Unit 有：
k * k * c 次乘法，以及 k * k * c - 1 次加法- 1
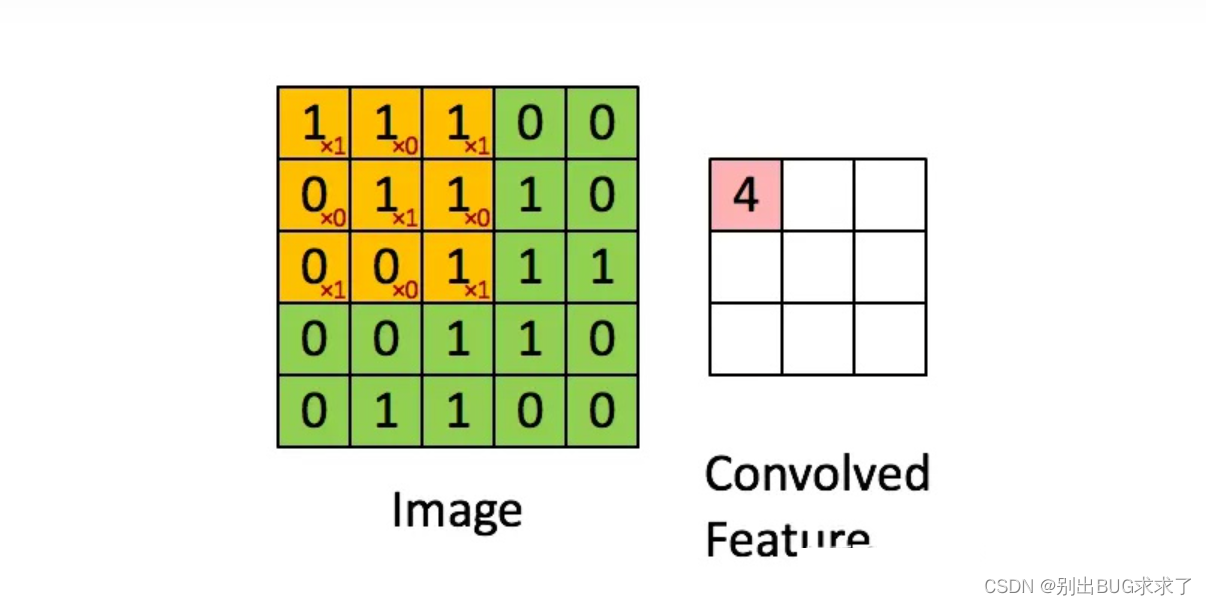
用上图形象化解释就是：
Image大小为 5x5，卷积核大小为 3x3，那么一次3x3的卷积（求右图矩阵一个元素的值）所需运算量：(3x3)个乘法+(3x3-1)个加法 = 17。要得到右图convolved feature （3x3的大小）：17x9 = 153
如果输出 feature map 的分辨率是 H * W ，且输出 o 个 feature map，则输出 feature map 包含 Unit的总数就是 H * W * o。
因此，该卷积层在计算 wx 时有:
k * k * c * H * W * o 次乘法 --（1） (k * k * c - 1) * H * W * o 次加法 --（2）- 1
- 2
再考虑偏置项 b 包含的计算量：
由于 b 只存在加法运算，输出 feature map 上的每个 Unit 做一次偏置项加法。因此，该卷积层在计算偏置项时总共包含：
H * W * o 次加法 --（3）- 1
将该卷积层的 wx 和 b 两部分的计算次数累计起来就有：
式(1) 次乘法:
k * k * c * H * W * o 次乘法- 1
式(2) + 式(3) 次加法:
(k * k * c - 1) * H * W * o + H * W * o = k * k * c * H * W * o- 1
可见，式(2) + 式(3) = 式 (1)
对于带偏置项的卷积层，乘法运算和加法运算的次数相等，刚好配对。定义一次加法和乘法表示一个flop，该层的计算力消耗 为：
k * k * c * H * W * o- 1
刚好等于图中两个立方体（绿色和橙色）体积的乘积。全连接层的算法也是一样。
（２）针对于池化层：
无参数
（３）针对于全连接层：
参数量＝计算量＝weight_in*weight_out- 1
（4）以 AlexNet为例，详解计算网络参数过程
1-网络结构
AlexNet整体的网络结构包括：1个输入层（input layer）、5个卷积层（C1、C2、C3、C4、C5）、2个全连接层（FC6、FC7）和1个输出层（output layer）。下面对网络结构详细介绍。
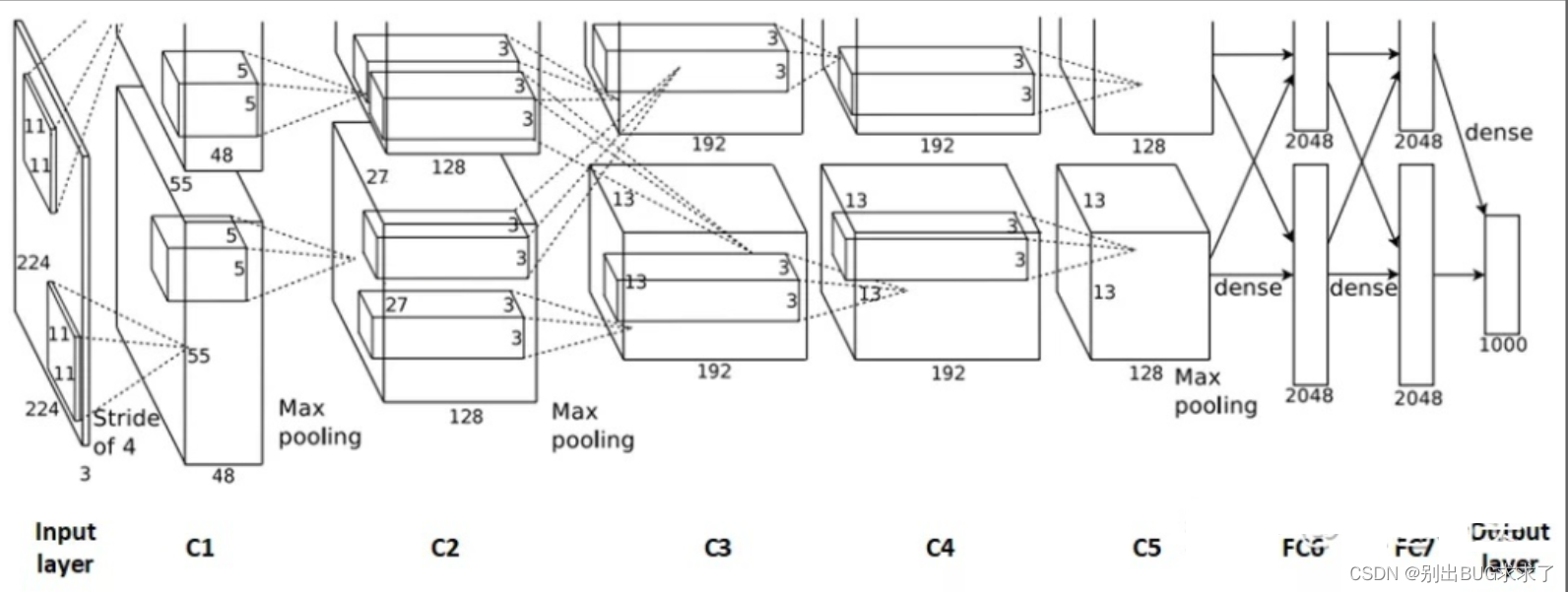
上面这张图就是AlexNet的网络结构。初看这张图有的读者可能会觉得有个疑问：网络上部分是不是没有画完？其实不是的。鉴于当时的硬件资源限制，由于AlexNet结构复杂、参数很庞大，难以在单个GPU上进行训练。因此AlexNet采用两路GTX 580 3GB GPU并行训练。也就是说把原先的卷积层平分成两部分FeatureMap分别在两块GPU上进行训练（例如卷积层55x55x96分成两个FeatureMap：55x55x48）。上图中上部分和下部分是对称的，所以上半部分没有完全画出来。值得一提的是，卷积层 C2、C4、C5中的卷积核只和位于同一GPU的上一层的FeatureMap相连，C3的卷积核与两个GPU的上一层的FeautureMap都连接。
1.1-输入层（Input layer）
原论文中，AlexNet的输入图像尺寸是224x224x3。但是实际图像尺寸为227x227x3。据说224x224可能是写paper时候的手误？还是后来对网络又做了调整？
1.2-卷积层（C1）
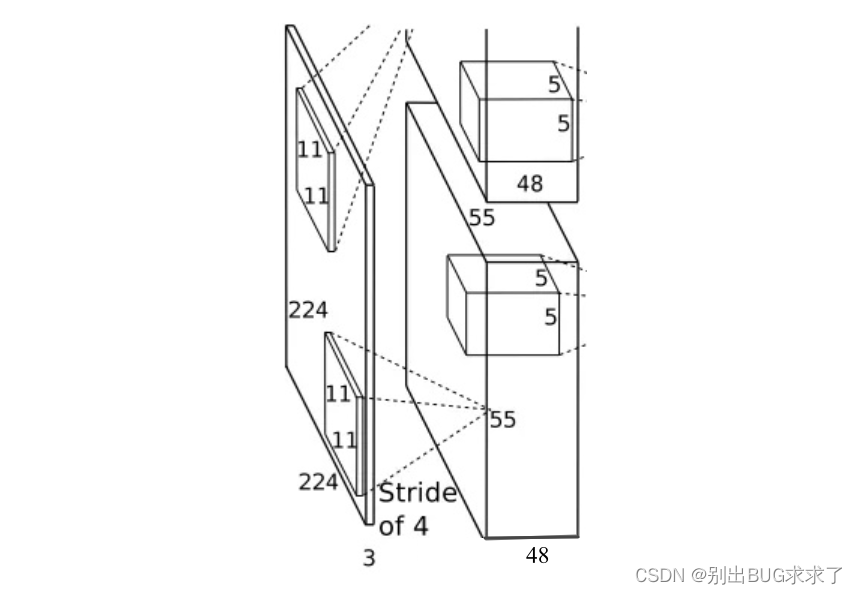
该层的处理流程是：卷积–>ReLU–>局部响应归一化（LRN）–>池化。
卷积：输入是227x227x3，使用96个11x11x3的卷积核进行卷积，padding=0，stride=4，根据公式：(input_size + 2 * padding - kernel_size) / stride + 1=(227+2*0-11)/4+1=55，得到输出是55x55x96。
ReLU： 将卷积层输出的FeatureMap输入到ReLU函数中。
局部响应归一化： 局部响应归一化层简称LRN，是在深度学习中提高准确度的技术方法。一般是在激活、池化后进行。LRN对局部神经元的活动创建竞争机制，使得其中响应比较大的值变得相对更大，并抑制其他反馈较小的神经元，增强了模型的泛化能力。
LRN的公式如下：
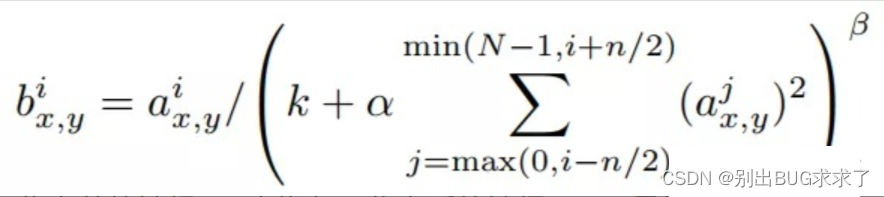
a为归一化之前的神经元，b为归一化之后的神经元；N是卷积核的个数，也就是生成的FeatureMap的个数；k，α，β，n是超参数，论文中使用的值是k=2，n=5，α=0.0001，β=0.75。局部响应归一化的输出仍然是55x55x96。将其分成两组，每组大小是55x55x48，分别位于单个GPU上。
**池化：**使用3x3，stride=2的池化单元进行最大池化操作（max pooling）。注意这里使用的是重叠池化，即stride小于池化单元的边长。根据公式：(55+2*0-3)/2+1=27，每组得到的输出为27x27x48。
1.3-卷积层（C2）
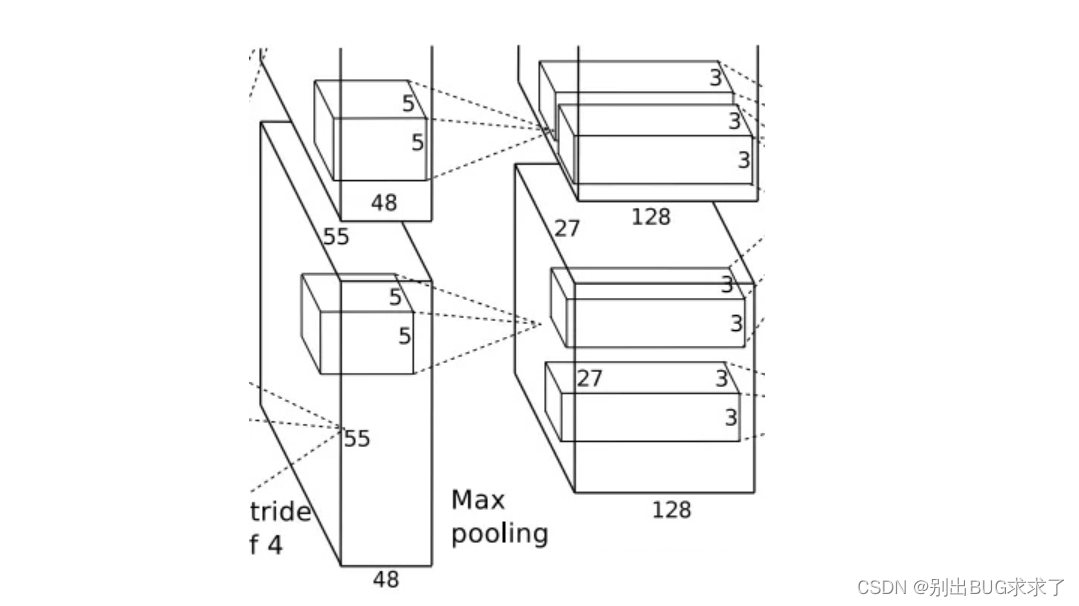
该层的处理流程是：卷积–>ReLU–>局部响应归一化（LRN）–>池化。卷积： 两组输入均是27x27x48，各组分别使用128个5x5x48的卷积核进行卷积，padding=2，stride=1，根据公式：(input_size + 2 * padding - kernel_size) / stride + 1=(27+2*2-5)/1+1=27，得到每组输出是27x27x128。
ReLU： 将卷积层输出的FeatureMap输入到ReLU函数中。
局部响应归一化： 使用参数k=2，n=5，α=0.0001，β=0.75进行归一化。每组输出仍然是27x27x128。
池化： 使用3x3，stride=2的池化单元进行最大池化操作（max pooling）。注意这里使用的是重叠池化，即stride小于池化单元的边长。根据公式：(27+2*0-3)/2+1=13，每组得到的输出为13x13x128。
1.4-卷积层（C3）
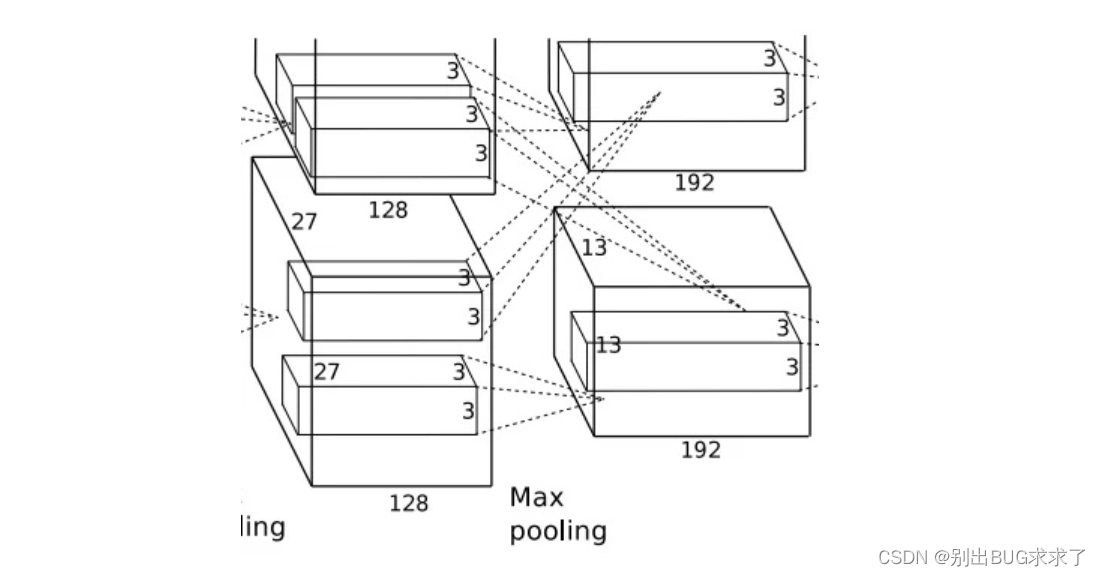
该层的处理流程是： 卷积–>ReLU卷积：输入是13x13x256，使用384个3x3x256的卷积核进行卷积，padding=1，stride=1，根据公式：(input_size + 2 * padding - kernel_size) / stride + 1=(13+2*1-3)/1+1=13，得到输出是13x13x384。
ReLU：将卷积层输出的FeatureMap输入到ReLU函数中。将输出其分成两组，每组FeatureMap大小是13x13x192，分别位于单个GPU上。
1.5-卷积层（C4）
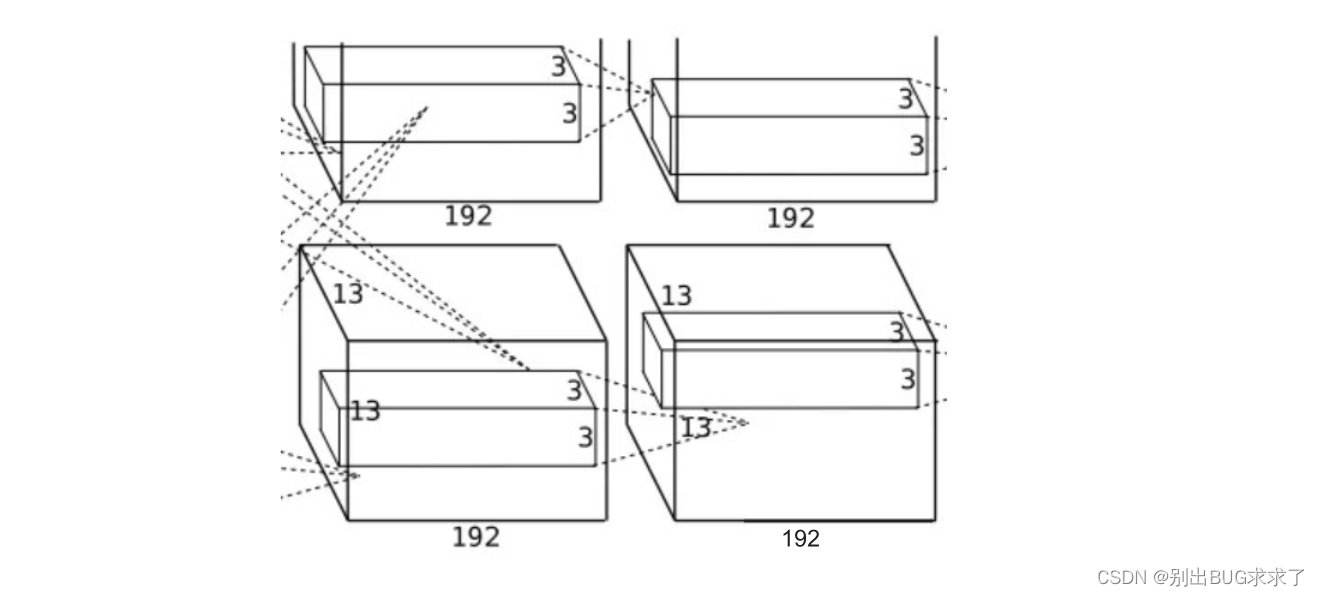
该层的处理流程是：卷积–>ReLU卷积： 两组输入均是13x13x192，各组分别使用192个3x3x192的卷积核进行卷积，padding=1，stride=1，根据公式：(input_size + 2 * padding - kernel_size) / stride + 1=(13+2*1-3)/1+1=13，得到每组FeatureMap输出是13x13x192。
ReLU： 将卷积层输出的FeatureMap输入到ReLU函数中。
1.6-卷积层（C5）
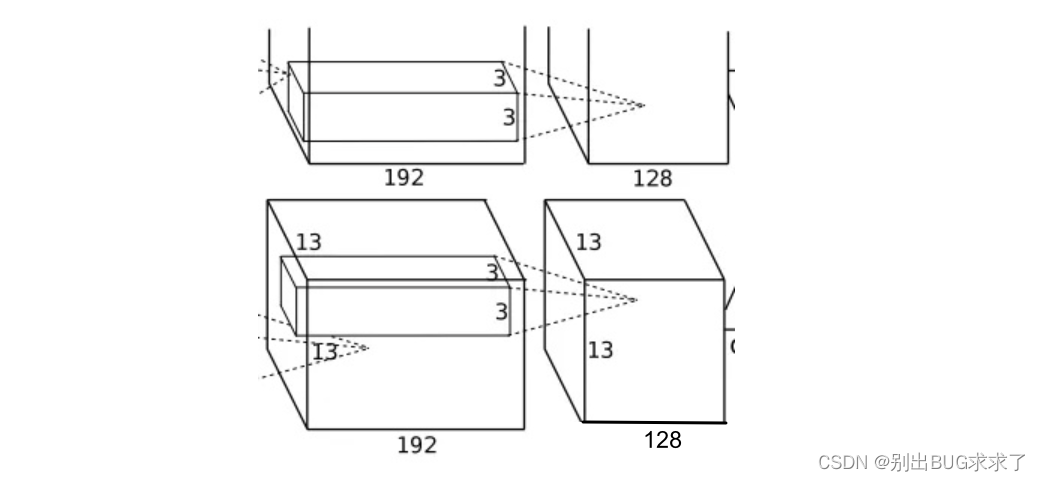
该层的处理流程是：卷积–>ReLU–>池化
卷积： 两组输入均是13x13x192，各组分别使用128个3x3x192的卷积核进行卷积，padding=1，stride=1，根据公式：(input_size + 2 * padding - kernel_size) / stride + 1=(13+2*1-3)/1+1=13，得到每组FeatureMap输出是13x13x128。
ReLU： 将卷积层输出的FeatureMap输入到ReLU函数中。
池化：使用3x3，stride=2的池化单元进行最大池化操作（max pooling）。注意这里使用的是重叠池化，即stride小于池化单元的边长。根据公式：(13+2*0-3)/2+1=6，每组得到的输出为6x6x128。
1.7-全连接层（FC6）
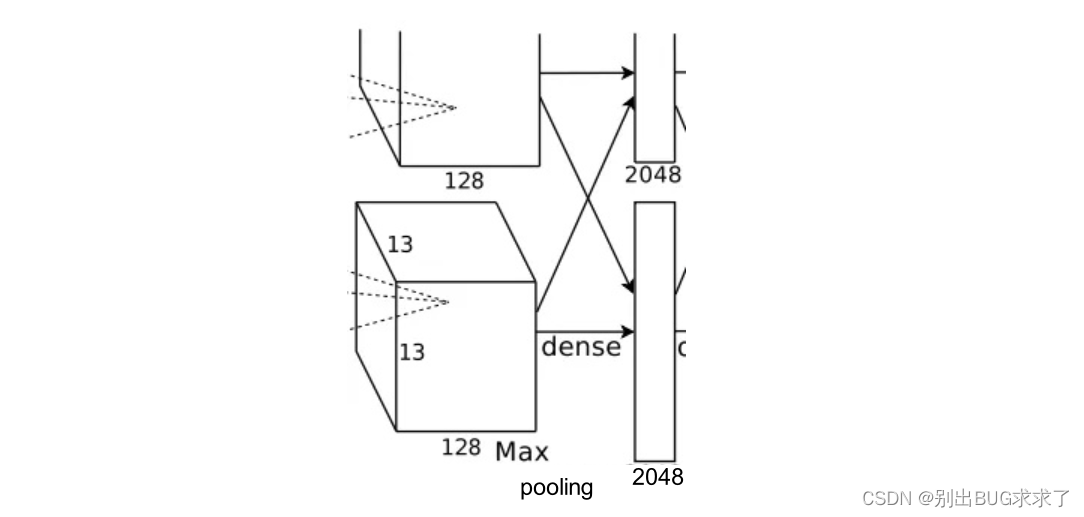
该层的流程为：（卷积）全连接 -->ReLU -->Dropout （卷积）
全连接：输入为6×6×256，使用4096个6×6×256的卷积核进行卷积，由于卷积核尺寸与输入的尺寸完全相同，即卷积核中的每个系数只与输入尺寸的一个像素值相乘一一对应，根据公式：(input_size + 2 * padding - kernel_size) / stride + 1=(6+2*0-6)/1+1=1，得到输出是1x1x4096。既有4096个神经元，该层被称为全连接层。
ReLU： 这4096个神经元的运算结果通过ReLU激活函数中。
Dropout： 随机的断开全连接层某些神经元的连接，通过不激活某些神经元的方式防止过拟合。4096个神经元也被均分到两块GPU上进行运算。
1.8-全连接层（FC7）
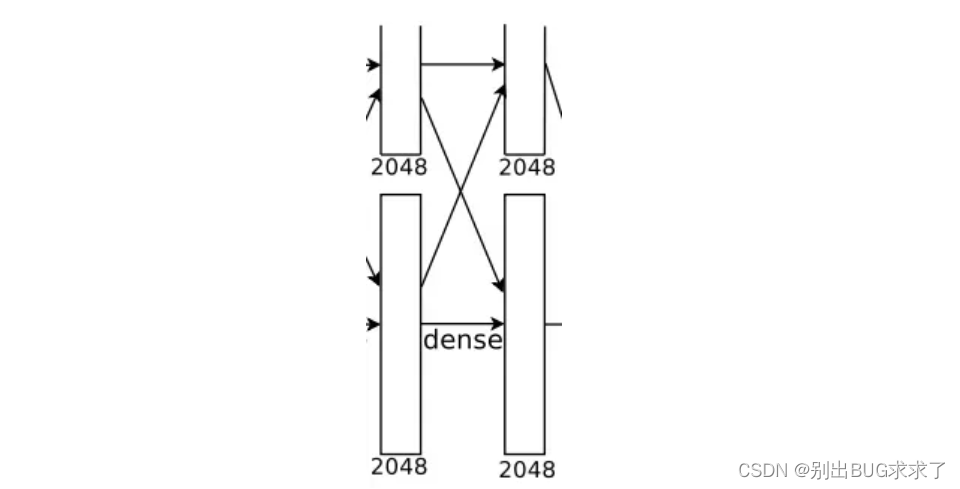
该层的流程为：（卷积）全连接 -->ReLU -->Dropout全连接： 输入为4096个神经元，输出也是4096个神经元（作者设定的）。
ReLU： 这4096个神经元的运算结果通过ReLU激活函数中。
Dropout： 随机的断开全连接层某些神经元的连接，通过不激活某些神经元的方式防止过拟合。
4096个神经元也被均分到两块GPU上进行运算。
1.9-输出层（Output layer）
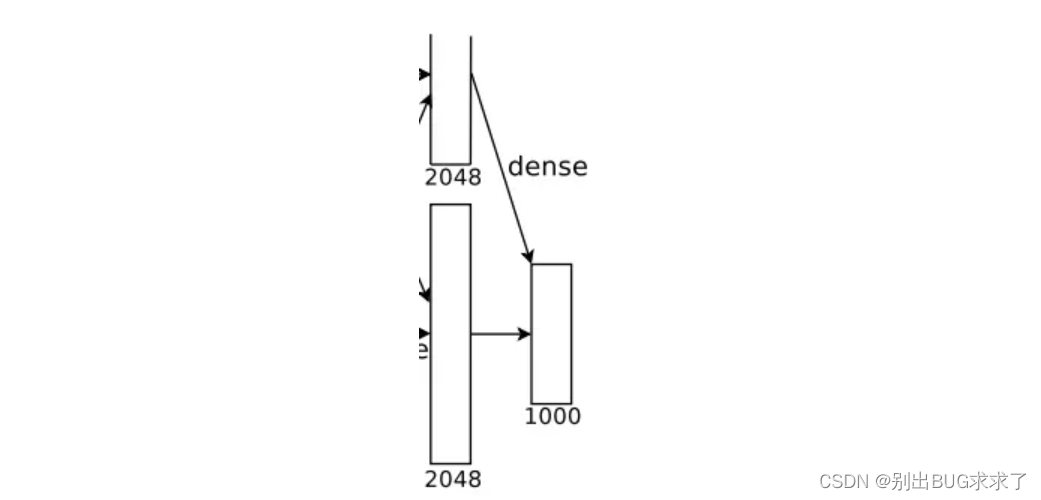
该层的流程为：（卷积）全连接 -->Softmax
全连接： 输入为4096个神经元，输出是1000个神经元。这1000个神经元即对应1000个检测类别。
Softmax： 这1000个神经元的运算结果通过Softmax函数中，输出1000个类别对应的预测概率值。
2-网络参数
2.1-AlexNet神经元数量
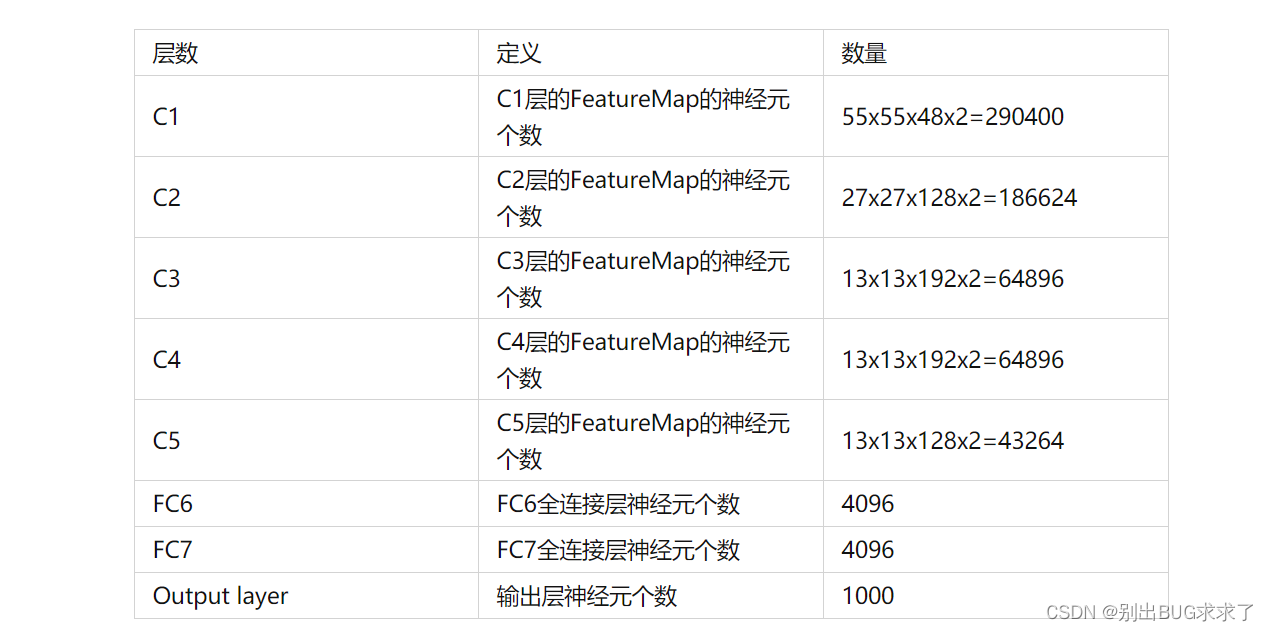
整个AlexNet网络包含的神经元个数为：290400 + 186624 + 64896 + 64896 + 43264 + 4096 + 4096 + 1000 = 659272
大约65万个神经元。
2.2-AlexNet参数数量
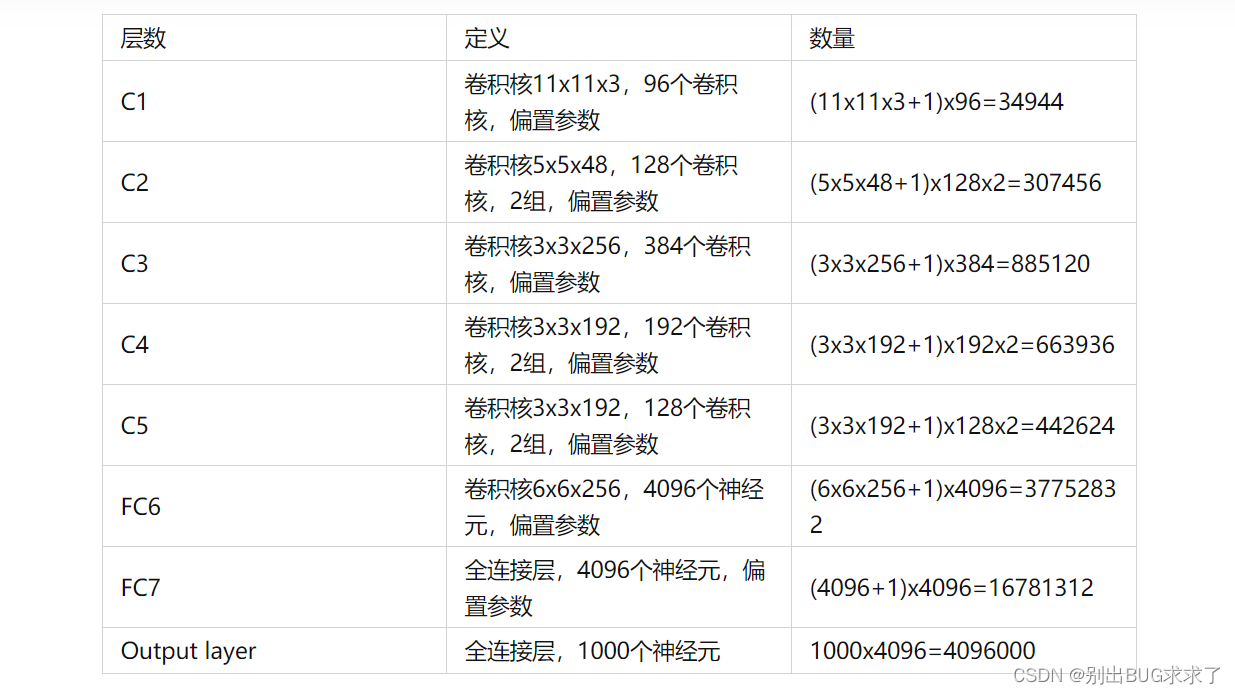
整个AlexNet网络包含的参数数量为：34944 + 307456 + 885120 + 663936 + 442624 + 37752832 + 16781312 + 4096000 = 60964224
大约6千万个参数。
设定每个参数是32位浮点数，每个浮点数4个字节。这样参数占用的空间为：
60964224 x 4 = 243856896(Byte) = 238141.5(Kb) = 232.56(Mb)
参数共占用了大约232Mb的空间。
2.3-FLOPs
FLOPS（即“每秒浮点运算次数”，“每秒峰值速度”），是“每秒所执行的浮点运算次数”（floating-point operations per second）的缩写。它常被用来估算电脑的执行效能，尤其是在使用到大量浮点运算的科学计算领域中。正因为FLOPS字尾的那个S，代表秒，而不是复数，所以不能省略掉。
FLOPS， 即每秒浮点运算次数, 是每秒所执行的浮点运算次数（Floating-point operations per second；缩写：FLOPS）的简称，被用来评估电脑效能.FLOPs： 注意s小写，是floating point operations的缩写（s表复数），意指浮点运算数，理解为计算量, 可以用来衡量算法/模型的复杂度。
常用框架的复杂度TOPS(Tera Operations Per Second)，1TOPS代表处理器每秒钟可进行一万亿次（10^12）操作
一个MFLOPS（megaFLOPS）等于每秒一佰万（=10^6）次的浮点运算， 一个GFLOPS（gigaFLOPS）等于每秒十亿（=10^9）次的浮点运算， 一个TFLOPS（teraFLOPS）等于每秒一万亿（=10^12）次的浮点运算，(1太拉) 一个PFLOPS（petaFLOPS）等于每秒一千万亿（=10^15）次的浮点运算， 一个EFLOPS（exaFLOPS）等于每秒一佰京（=10^18）次的浮点运算。- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
在AlexNet网络中，对于卷积层，FLOPS=num_params∗(H∗W)。其中num_params为参数数量，H*W为卷积层的高和宽。对于全连接层，FLOPS=num_params。
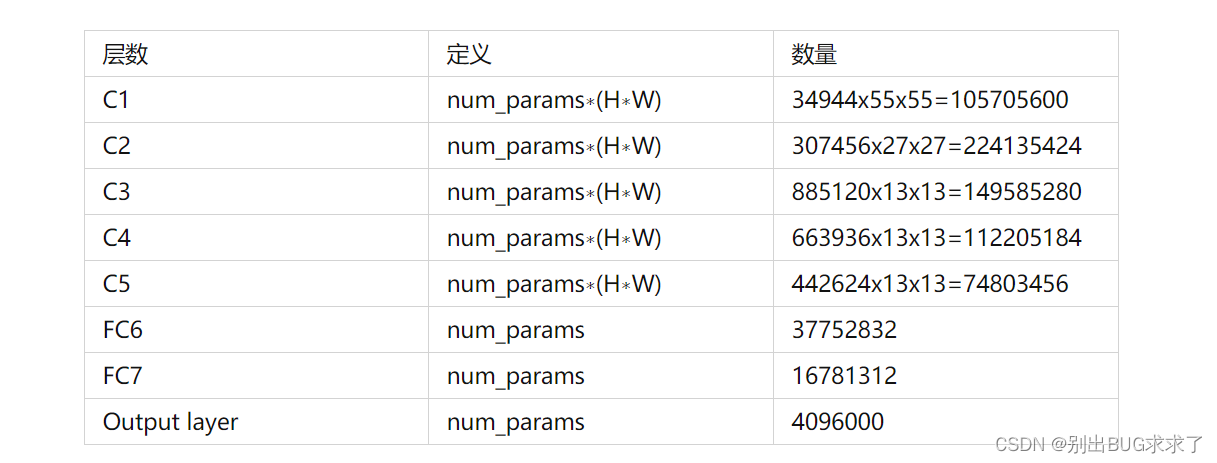
AlexNet整体的网络结构，包含各层参数个数、FLOPS如下图所示：
3 对于换算计算量
-
一般一个参数是值一个float，也就是４个字节
-
1kb=1024字节
4 对于各个经典网络：
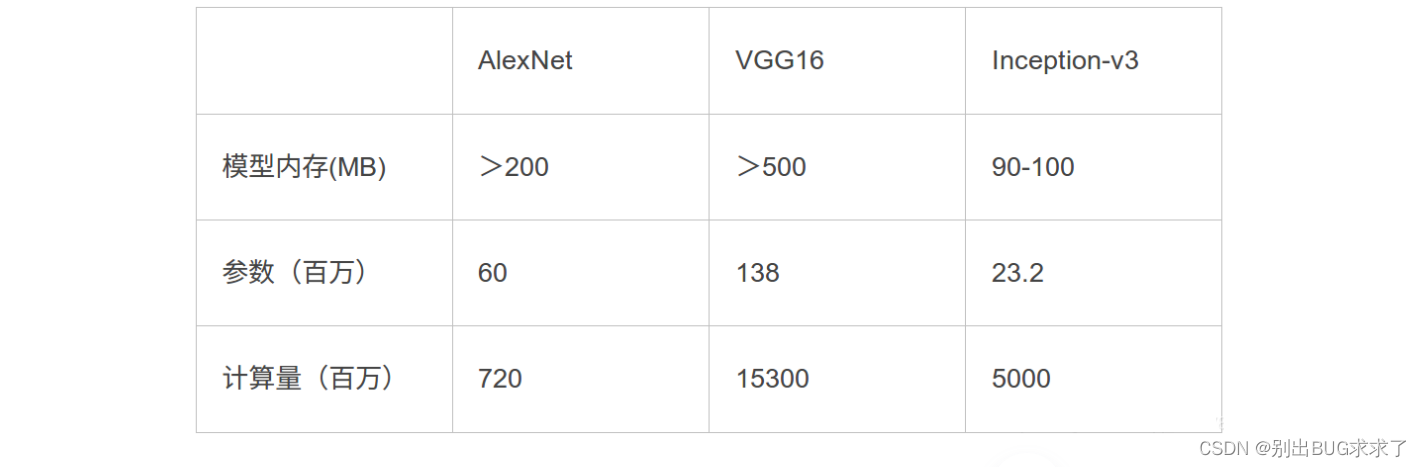
(1)换算
以alexnet为例：
参数量：6000万
设每个参数都是float,也就是一个参数是4字节，
总的字节数是24000万字节
24000万字节= 24000万/1024/1024=228mb
(2)为什么模型之间差距这么大
这个关乎于模型的设计了，其中模型里面最费参数的就是全连接层，这个可以看alex和vgg,
alex,vgg有很多fc(全连接层)
resnet就一个fc
inceptionv1(googlenet)也是就一个fc
(3)计算量
densenet其实这个模型不大，也就是参数量不大，因为就1个fc
但是他的计算量确实很大，因为每一次都把上一个feature加进来，所以计算量真的很大
5 计算量与参数量对于硬件要求
计算量，参数量对于硬件的要求是不同的
计算量的要求是在于芯片的floaps（指的是gpu的运算能力）
参数量取决于显存大小
6 计算量(FLOPs)和参数量(Params)
6.1 第一种方法：thop
详见GitHub开源：https://github.com/Lyken17/pytorch-OpCounter
计算量：
FLOPs，FLOP时指浮点运算次数，s是指秒，即每秒浮点运算次数的意思，考量一个网络模型的计算量的标准。参数量：
Params，是指网络模型中需要训练的参数总数。使用说明：
- 第一步：安装模块
pip install thop- 1
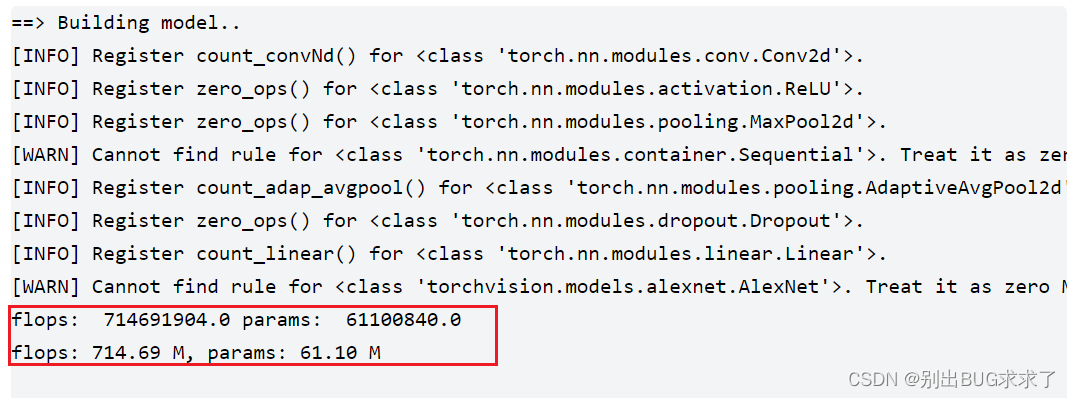
- 第二步：计算
# -- coding: utf-8 -- import torch import torchvision from thop import profile # Model print('==> Building model..') model = torchvision.models.alexnet(pretrained=False) dummy_input = torch.randn(1, 3, 224, 224) flops, params = profile(model, (dummy_input,)) print('flops: ', flops, 'params: ', params) print('flops: %.2f M, params: %.2f M' % (flops / 1000000.0, params / 1000000.0))- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
或者：
from torchvision.models import resnet18 from thop import profile model = resnet18() input = torch.randn(1, 3, 224, 224) #模型输入的形状,batch_size=1 flops, params = profile(model, inputs=(input, )) print(flops/1e9,params/1e6) #flops单位G，para单位M- 1
- 2
- 3
- 4
- 5
- 6
结果:
注意：
输入input的第一维度是批量(batch size)，批量的大小不回影响参数量， 计算量是batch_size=1的倍数
profile(net, (inputs,))的 (inputs,)中必须加上逗号，否者会报错6.2 第二种方法：ptflops
# -- coding: utf-8 -- import torchvision from ptflops import get_model_complexity_info model = torchvision.models.alexnet(pretrained=False) flops, params = get_model_complexity_info(model, (3, 224, 224), as_strings=True, print_per_layer_stat=True) print('flops: ', flops, 'params: ', params)- 1
- 2
- 3
- 4
- 5
- 6
- 7
结果：
AlexNet( 61.101 M, 100.000% Params, 0.716 GMac, 100.000% MACs, (features): Sequential( 2.47 M, 4.042% Params, 0.657 GMac, 91.804% MACs, (0): Conv2d(0.023 M, 0.038% Params, 0.07 GMac, 9.848% MACs, 3, 64, kernel_size=(11, 11), stride=(4, 4), padding=(2, 2)) (1): ReLU(0.0 M, 0.000% Params, 0.0 GMac, 0.027% MACs, inplace=True) (2): MaxPool2d(0.0 M, 0.000% Params, 0.0 GMac, 0.027% MACs, kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False) (3): Conv2d(0.307 M, 0.503% Params, 0.224 GMac, 31.316% MACs, 64, 192, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2)) (4): ReLU(0.0 M, 0.000% Params, 0.0 GMac, 0.020% MACs, inplace=True) (5): MaxPool2d(0.0 M, 0.000% Params, 0.0 GMac, 0.020% MACs, kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False) (6): Conv2d(0.664 M, 1.087% Params, 0.112 GMac, 15.681% MACs, 192, 384, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (7): ReLU(0.0 M, 0.000% Params, 0.0 GMac, 0.009% MACs, inplace=True) (8): Conv2d(0.885 M, 1.448% Params, 0.15 GMac, 20.902% MACs, 384, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (9): ReLU(0.0 M, 0.000% Params, 0.0 GMac, 0.006% MACs, inplace=True) (10): Conv2d(0.59 M, 0.966% Params, 0.1 GMac, 13.936% MACs, 256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (11): ReLU(0.0 M, 0.000% Params, 0.0 GMac, 0.006% MACs, inplace=True) (12): MaxPool2d(0.0 M, 0.000% Params, 0.0 GMac, 0.006% MACs, kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False) ) (avgpool): AdaptiveAvgPool2d(0.0 M, 0.000% Params, 0.0 GMac, 0.001% MACs, output_size=(6, 6)) (classifier): Sequential( 58.631 M, 95.958% Params, 0.059 GMac, 8.195% MACs, (0): Dropout(0.0 M, 0.000% Params, 0.0 GMac, 0.000% MACs, p=0.5, inplace=False) (1): Linear(37.753 M, 61.788% Params, 0.038 GMac, 5.276% MACs, in_features=9216, out_features=4096, bias=True) (2): ReLU(0.0 M, 0.000% Params, 0.0 GMac, 0.001% MACs, inplace=True) (3): Dropout(0.0 M, 0.000% Params, 0.0 GMac, 0.000% MACs, p=0.5, inplace=False) (4): Linear(16.781 M, 27.465% Params, 0.017 GMac, 2.345% MACs, in_features=4096, out_features=4096, bias=True) (5): ReLU(0.0 M, 0.000% Params, 0.0 GMac, 0.001% MACs, inplace=True) (6): Linear(4.097 M, 6.705% Params, 0.004 GMac, 0.573% MACs, in_features=4096, out_features=1000, bias=True) ) ) flops: 0.72 GMac params: 61.1 M- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
6.3 第三种方法：pytorch_model_summary
import torch import torchvision from pytorch_model_summary import summary # Model print('==> Building model..') model = torchvision.models.alexnet(pretrained=False) dummy_input = torch.randn(1, 3, 224, 224) print(summary(model, dummy_input, show_input=False, show_hierarchical=False))- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
结果：
==> Building model.. ----------------------------------------------------------------------------- Layer (type) Output Shape Param # Tr. Param # ============================================================================= Conv2d-1 [1, 64, 55, 55] 23,296 23,296 ReLU-2 [1, 64, 55, 55] 0 0 MaxPool2d-3 [1, 64, 27, 27] 0 0 Conv2d-4 [1, 192, 27, 27] 307,392 307,392 ReLU-5 [1, 192, 27, 27] 0 0 MaxPool2d-6 [1, 192, 13, 13] 0 0 Conv2d-7 [1, 384, 13, 13] 663,936 663,936 ReLU-8 [1, 384, 13, 13] 0 0 Conv2d-9 [1, 256, 13, 13] 884,992 884,992 ReLU-10 [1, 256, 13, 13] 0 0 Conv2d-11 [1, 256, 13, 13] 590,080 590,080 ReLU-12 [1, 256, 13, 13] 0 0 MaxPool2d-13 [1, 256, 6, 6] 0 0 AdaptiveAvgPool2d-14 [1, 256, 6, 6] 0 0 Dropout-15 [1, 9216] 0 0 Linear-16 [1, 4096] 37,752,832 37,752,832 ReLU-17 [1, 4096] 0 0 Dropout-18 [1, 4096] 0 0 Linear-19 [1, 4096] 16,781,312 16,781,312 ReLU-20 [1, 4096] 0 0 Linear-21 [1, 1000] 4,097,000 4,097,000 ============================================================================= Total params: 61,100,840 Trainable params: 61,100,840 Non-trainable params: 0 ------------------------------------------------------------------------------ 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
6.4 第四种方法：参数总量和可训练参数总量
import torch import torchvision from pytorch_model_summary import summary # Model print('==> Building model..') model = torchvision.models.alexnet(pretrained=False) pytorch_total_params = sum(p.numel() for p in model.parameters()) trainable_pytorch_total_params = sum(p.numel() for p in model.parameters() if p.requires_grad) print('Total - ', pytorch_total_params) print('Trainable - ', trainable_pytorch_total_params)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
结果：
7 输入数据对模型的参数量和计算量的影响
# -- coding: utf-8 -- import torch import torchvision from thop import profile # Model print('==> Building model..') model = torchvision.models.alexnet(pretrained=False) dummy_input = torch.randn(1, 3, 224, 224) flops, params = profile(model, (dummy_input,)) print('flops: ', flops, 'params: ', params) print('flops: %.2f M, params: %.2f M' % (flops / 1000000.0, params / 1000000.0))- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 输入数据：(1, 3, 224, 224)，一张224*224的RGB图像
-
输入数据：(1, 3, 512, 512)，一张512*512的RGB图像
-
输入数据：(8, 3, 224, 224)，八张224*224的RGB图像
-
相关阅读:
Pandas数据分析：快速图表可视化各类操作详解+实例代码(一)
桌面应用开发有哪些主流框架？
day49【动态规划】买卖股票的最佳时机问题
15：00面试，15：08就出来了，问的问题有点变态。。。
【物理应用】水下浮动风力涡轮机的尾流诱导动态模拟风场附matlab代码
Hbase安装（保姆级）---------yarn逻辑解析
一比一还原axios源码（三）—— 错误处理
2、树相关算法
【Android】带下划线的TextView
解决Permission is not allowed后基于Ubuntu23.04安装配置docker与docker-compose
- 原文地址：https://blog.csdn.net/weixin_39589455/article/details/127261338
