[EECS][Design Lab 3][All Carrot, No Stick] 实现目标线性轨迹运动 实现状态机的级联 距离控制实现避障

Assume that pose0 = util.Pose(x0,y0,theta0), then pose0.point() returns a point equal to util.Point(x0,y0).

These procedures may also be useful:

• util.nearAngle(angle1, angle2, angleEps),
• util.fixAnglePlusMinusPi(angle), and
• util.clip(value, minValue, maxValue).

For reference, we should also consult the Lab Infrastructure Guide. It’s a good place to go to remind ourself about how robots and brains work.

Step2.3 Driving to a point

Objective: Implement the DynamicMoveToPoint state machine, which directs the ro­bot to perform an action to reach a goal Point.

Remember that the input to the DynamicMoveToPoint state machine is a tuple (goalPoint, sensors), where

• goalPoint is an instance of util.Point. This point specifies where the robot should drive (in the coordinate frame of the odometry).
• sensors is an instance of io.SensorInput. You can get the current odometry value with sen­sors.odometry, which is an instance of util.Pose.

The output of the DynamicMoveToPoint state machine should be an instance of io.Action that specifies the action to be taken by the robot during its next step. For example, to create an ac­tion with forward velocity 0.2 m/s and rotational velocity 0.1 radians/s, the output should be io.Action(fvel=0.2, rvel=0.1).

The robot should follow a (nearly) straight line from its current position to its goal point.

S2

Determine the action that should be output by the DynamicMoveToPoint state machine for the following input conditions. (Answers can simple commands such as ’move forward’ or ’rotate left’).

Think of a strategy for implementing the DynamicMoveToPoint state machine. Explain how that strategy will drive the robot to the goal point. The output of our state machine should depend only on the input ; it doesn’t need to use the state.

S3

Write code to implement our strategy in the file dynamicMoveToPointSkeleton.py.

1. First, test our code in idle, as follows. Open the file dynamicMoveToPointSkeleton.py,

   comment out

from soar.io import io 
1

​ and uncomment

import lib601.io as io 
1

Now, test the code in idle, by running the testMove procedure from testMove.py.

The test here has little impact on the following simulation and real car, so we won’t explain too much here

After our code works in idle, go back to soar’s version of io.py by editing dynamicMoveToPointSkeleton.py and commenting out

import lib601.io as io 
1

and uncommenting

from soar.io import io 
1

Now, test it using soar, by running moveBrainSkeleton.py in the simulated world bigEmp­tyWorld.py. Note that if we drag the robot around with your
mouse, the robot won’t know that it has been moved.

For help in debugging, find the line verbose = False in the brain and change it to verbose = True;

that will cause soar to print out a lot of information on each step of the state machine that controls the brain.

The moving track diagram of the car is as follows. At the beginning, the points are sparse because the car is fast, and then the points become more and more dense as the speed slows down.

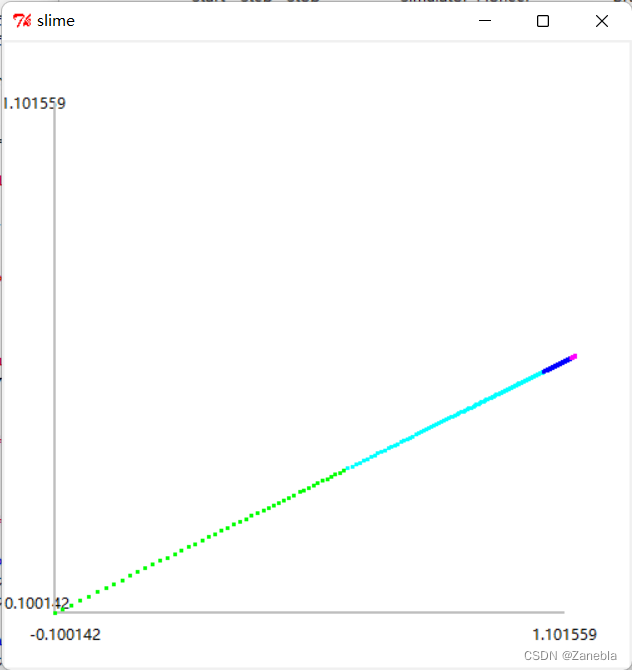
Step3 Hip to be Square

Objective: Make the robot move in a square. Accomplish this (and other cool robot moves) by defining a new state machine class FollowFigure, which serves the role of being a GoalGenerator.

When we initialize the FollowFigure state machine, we will give it a list of way points, which are points that define a sequence of linear segments that the robot should traverse. The job of FollowFigure is to take instances of io.SensorInput as input and generate instances of util.Point as output; it should start out by generating the first point in the input sequence as output, and do that until the robot’s actual pose (found as sensorInput.odometry) is near that point; once the robot has gotten near the target point, the machine should switch to generating the next target point as output, etc. Even after the robot gets near the final point, the machine should just continue to generate that point as output.

So, for example, if we were to use the FollowFigure instance below as our target generator, it should cause the robot to move in a square.

squarePoints = [util.Point(0.5, 0.5), util.Point(0.0, 1.0), 
util.Point(-0.5, 0.5), util.Point(0.0, 0.0)] 
FollowFigure(squarePoints)
1
2
3

If the robot is trying to follow the square above, and the FollowFigure state machine starts in its start state and sees odometry poses as input in the following sequence, what should its next state and output be on each step? The answer is as follows.

Define our FollowFigure state machine class in ffSkeleton.py. Test it in idle by running the testFF procedure in testFF.py, which contains the test cases shown above.

We do not explain here, mainly based on the simulation image results.

First, the code is as follows:

import lib601.sm as sm
import lib601.util as util
import math

from soar.io import io

class FollowFigure(sm.SM):
    def __init__(self, square):
        self.square = square
        self.index = 0

    startState = 'rotate'

    def getNextValues(self, state, inp):
        p = self.square[self.index]
        print 'Next goal -->', p 
        pp = inp.odometry
        mypoint = pp.point()
        inp = (p, mypoint)
        rotation_angle = mypoint.angleTo(p)
        actual_angle = util.fixAnglePlusMinusPi(pp.theta)
        print 'DynamicMoveToPoint', 'state=', state, 'inp=', inp

        rovel = abs(0.05 * rotation_angle)
        forvel = 0.15 * mypoint.distance(p)
        angle_eps = 0.005
        distance_eps = 0.005

        min_distance = min(io.SensorInput().sonars)
        if min_distance < 0.3:
            return('avoid',io.Action(fvel = 0, rvel = 0))

        if state == 'rotate':
            if util.nearAngle(rotation_angle, actual_angle, angle_eps):
                return('forward', io.Action(fvel = forvel, rvel = 0))
            else:
                return('rotate', io.Action(fvel = 0, rvel = rovel))

        if state == 'forward':
            if mypoint.isNear(p, distance_eps):
                return('stop', io.Action(fvel = 0, rvel = 0))
            else:
                return('forward', io.Action(fvel = forvel, rvel = 0))            

        if state == 'stop':
            self.index = self.index + 1
            if self.index == len(self.square):
                self.index = 0
                return('stop', io.Action(fvel = 0, rvel = 0))
            else:
                return('rotate', io.Action(fvel = 0, rvel = rovel))

        if state == 'avoid':
            if min_distance >= 0.3:
                return('rotate', io.Action(fvel = 0, rvel = rovel))
            if min_distance < 0.3:
                return('avoid',io.Action(fvel = 0, rvel = 0))
            

        return(state, io.Action())

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

Use the original sequence

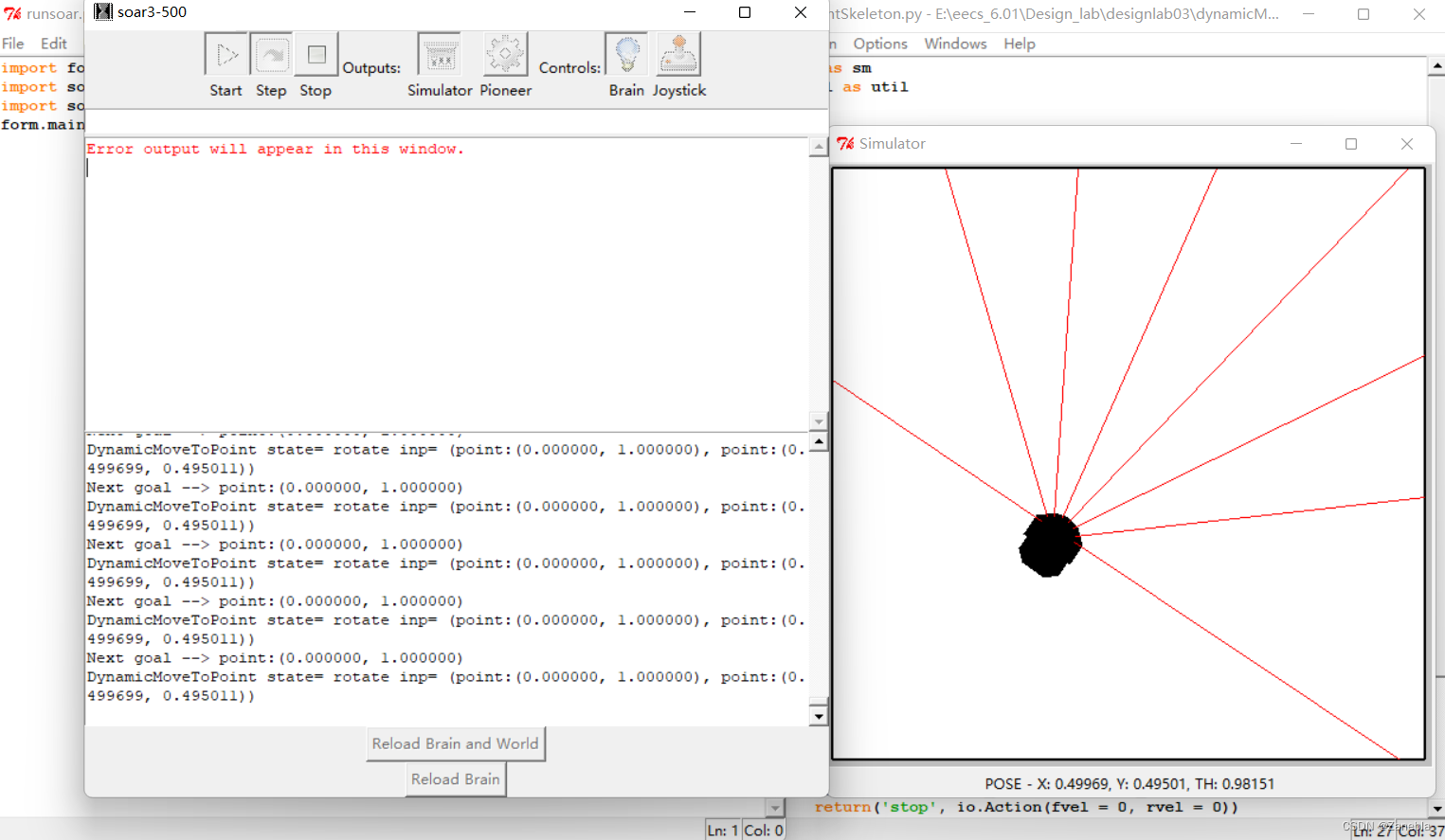
The image and data of car simulation

The final trajectory of the car is as follows

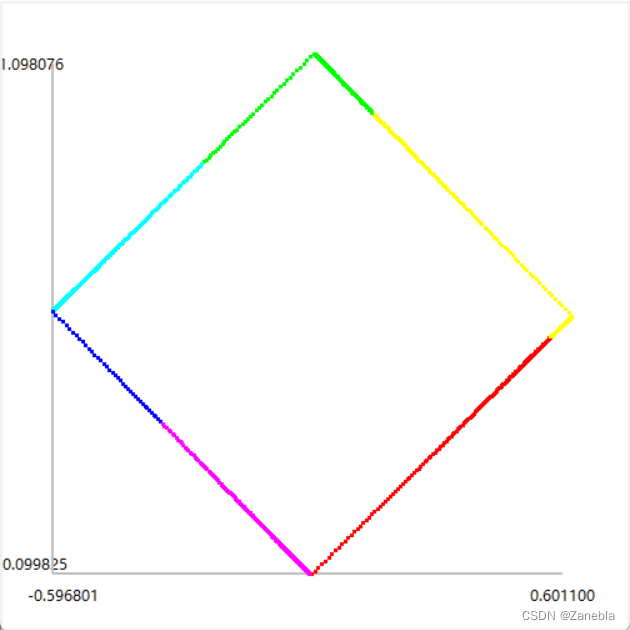
Change the sequence of ours

Reload the brain and world, run the soar again, The final trajectory of the car is as follows

Sorry, I lost my screenshot

Substitute an instance of the FollowFigure class for the GoalGenerator into the overall control architecture in moveBrainSkeleton.py, and debug it in bigEmptyWorld.py. Instead of going in a square, you could have your robot do a cool dance!

Step4 Avoiding Pedestrians

Objective: Your simulated robot, as it is currently constructed, tries to follow the spec­ified figure and completely ignores its sonar sensors. We would like to de­fine a new behavior that tries to follow the figure, but that monitors the front sonars and if any of them gets a reading less than 0.3, stops until the obstacle disappears, and then continues to follow the figure.

We can test this brain in simulation by dragging the robot around; its odometry reading won’t reflect that it has been dragged (it is as if you picked the robot up and ’kidnapped it’) so if we move it in front of a wall it should stop; and if we drag it away it should start to move again.

In the above code we have achieved this effect by setting a state “avoid” .

        min_distance = min(io.SensorInput().sonars)
        if min_distance < 0.3:
            return('avoid',io.Action(fvel = 0, rvel = 0))
1
2
3

        if state == 'avoid':
            if min_distance >= 0.3:
                return('rotate', io.Action(fvel = 0, rvel = rovel))
            if min_distance < 0.3:
                return('avoid',io.Action(fvel = 0, rvel = 0))
1
2
3
4
5

Step5 I am a ballerina

The final trajectory of the car is as follows

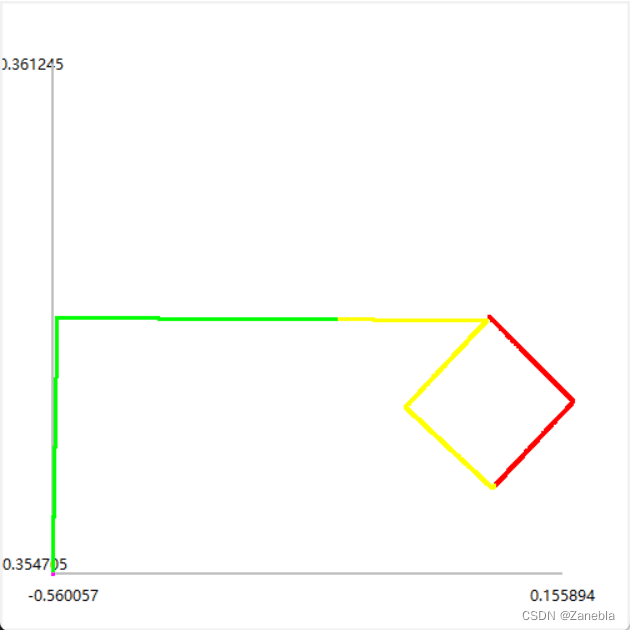
Step6 Conclusion and reflection

Compared with the previous experiment of walking along the wall, this experiment is easier to come up with a general framework, and the difficulty lies in the grasp of speed and error.

In addition, we also need to strengthen the data structure and algorithm foundation, so as to write more efficient and elegant code, and try our best to avoid the confusion of classes and objects, so as to make the code logic clearer