拓展上机课题解22/10/21

上课流程：

• 分析题目
• 演示样例
• 参数化式子
• 打代码

题目

以拆环为例子，上环的推导就不写了

演示样例

课上演示，略

参数化过程，形成递归式子

我们现在要拆n个环，假设我们已经成功完成n-1环的拆解，那么拆n环就是拆掉第n环后完成n-1环的拆解，所以问题就变成了怎么拆掉第n环。

图一：初始n环。

图二：题目说，除了第一环可以直接动，其它环装上或卸下的条件是：在它的前面仅有紧靠它那一个环在钗上。

所以如果要拆第n环就要只剩n环和n-1环（n≠1）。
所以先把前n-2环拆掉（我们都会拆n-1环怎么不会拆n-2环呢）。

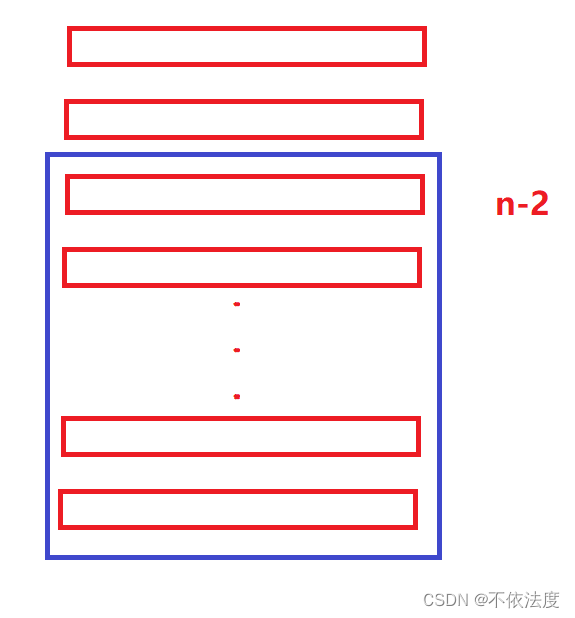
图三：只剩第n环和第n-1环。这时候第n个环可以拆了。

图四：拆掉第n环只剩第n-1环

图五：但是要拆第n-1环就得有第n-2环，所以再装上前n-2环，这下就成n-1环，也就是我们开始假设我们能成功拆解的环数。（发现没有，这和图一的初始状态就差不多了，差别就在于一个初始n环一个初始n-1环，所以图一到图四就是一个问题的分解过程，没理解不碍事，我们再来一遍）

我们现在要拆n-1环，假设我们已经成功完成n-2环的拆解，那么拆n-1环就是拆掉第n-1环后再完成n-2环的拆解（怎么拆n-2环我们假设已解决），所以问题就变成了怎么拆掉第n-1环。

当只剩n-1环和n-2环就可以拆掉n-1环。

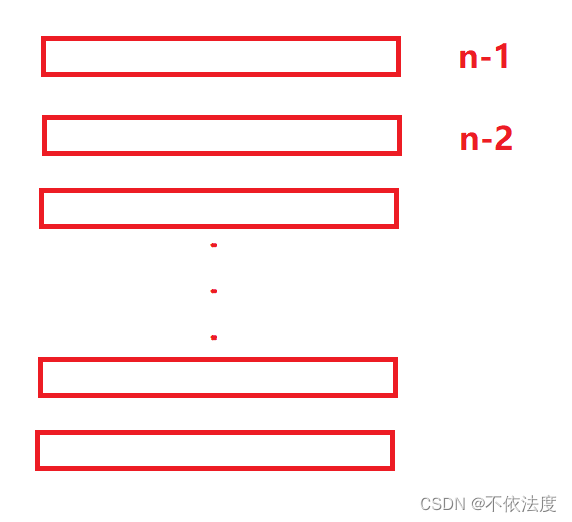
图六：拆掉第n-1环，但这时候剩了一个第n-2环，我们掌握了n-2环的拆解，所以我们让剩下的环变成n-2环，也就是装上n-3环。

图七、八：问题又变成了拆n-2环。拆n-2环就是拆掉第n-2环后拆n-3环（假设已掌握）。

---

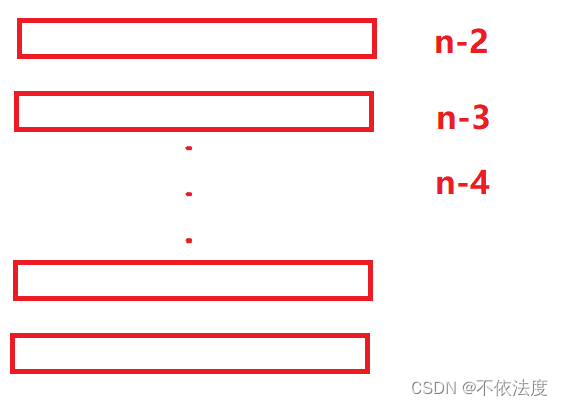
后面的操作基本一致，但是要注意到递归的临界点，当只剩第二环和第一环的时候，卸了第二环，第一环也可以直接卸（只剩2环这个拆解操作我们真的会，不用假设了）。

由上面的操作可以看出来：（每一行是一个周期操作）

• 拆n环=拆n-2环，卸第n环（直接可以操作），卸第n-1环（还不行）
• 拆n-1环=拆n-3环，卸第n-1环，卸第n-2环拆
• n-2环=拆n-4环，卸第n-2环，卸第n-3环
• …
• 拆4环=拆2环，卸第4环，卸第3环
• 拆3环=拆1环，卸第3环，卸第2环
• 拆2环=拆2环，卸1环（结束）

代码参考

#include
void down(int x){//拆前x环
    if(x<=0) return;//不能少，因为x=2式会经历down(x-2)=down(0)
    else if(x==1){
        printf("%d: D\n",x);
    }
    else{
        down(x-2);//先把前x-2环拆掉
        printf("%d: D\n",x);//只剩第x-1环和第x环，可以拆第x环
        up(x-2);//只剩第x-1环，但是拆第x-1环需要有第x-2环，所以上前x-2环
        down(x-1);//再拆前x-1环
    }
}
void up(int x){//上前x环
    if(x<=0) return;
    else if(x==1){
        printf("%d: U\n",x);
    }
    else{
        up(x-1);
        down(x-2);
        printf("%d: U\n",x);
        up(x-2);
    }
}
int main(){
    int k;
    char c;
    scanf("%d %c",&k,&c);
    switch(c){
        case 'D':
            down(k);
            break;
        case 'U':
            up(k);
            break;
    }    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

顺便附上L2-2，L2-3动态规划的代码

学有余力的同学可以写一下这两题（用递归的方式写，如果有兴趣的可以简单了解一下动态规划的理念，这里仅提供后两题动态规划的写法）

L2-2

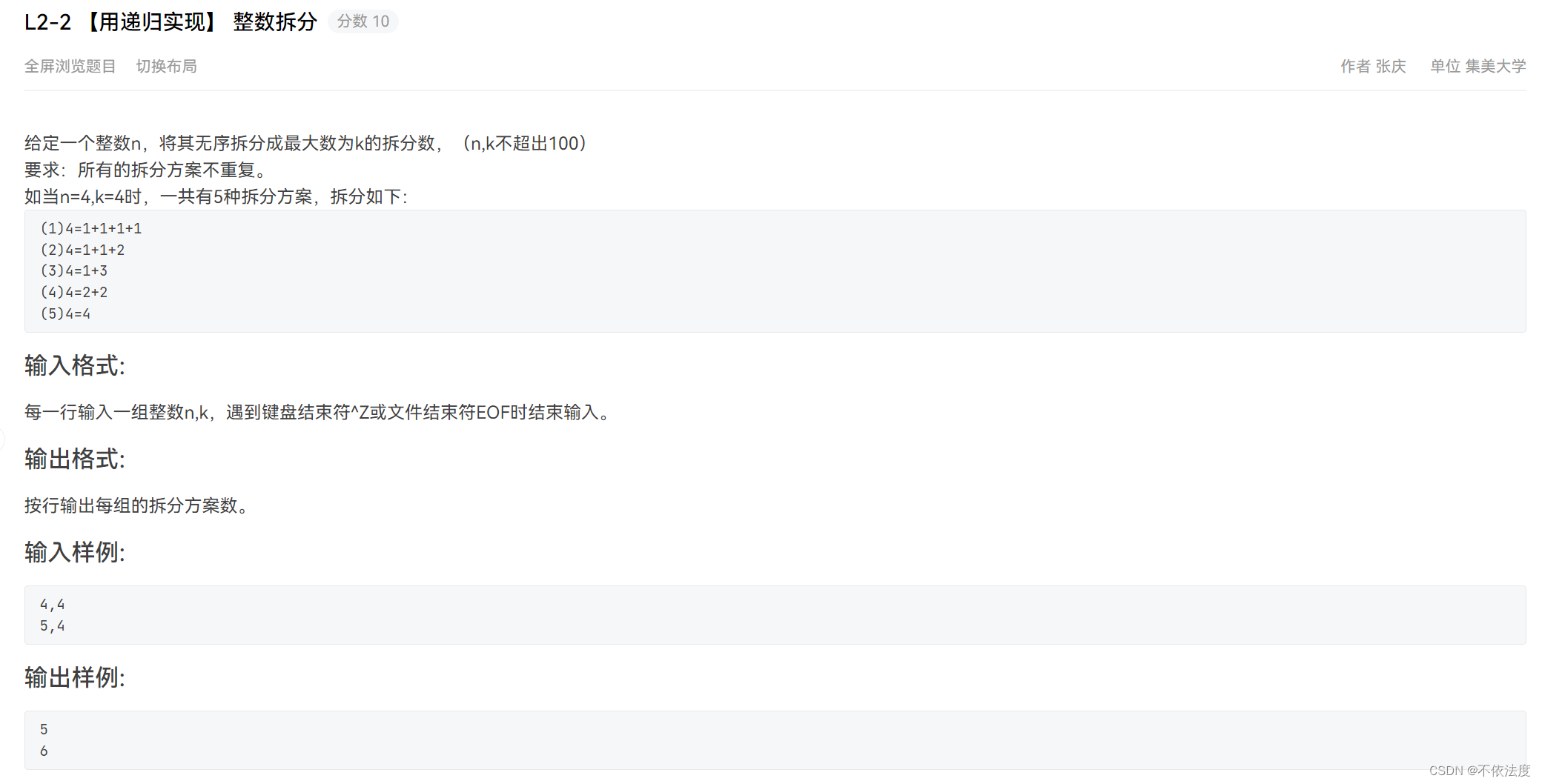
把递归公式列出来就没什么问题了

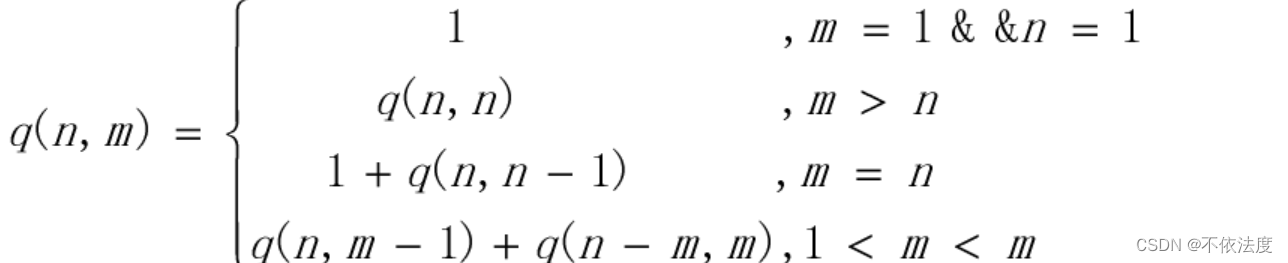
前两个式子很好理解，不提了。第四个式子解释一下（第三个公式是第四个公式的特殊化），把整数n拆分，拆分后的数最大为m，有两种情况。①拆分数中包含m。 ②拆分数中不包含m。

1. 一定要包含m，那就提一个m出来。 { { x 1 , x 2 , x 3 . . . x k } , m } \{\{x_1,x_2,x_3...x_k\},m\} {{x1​,x2​,x3​...xk​},m}， { x 1 , x 2 , x 3 . . . x k } \{x_1,x_2,x_3...x_k\} {x1​,x2​,x3​...xk​}的和为$n-m$，所以包含$m$的拆分方式有$q(n-m,m)$。$x_i$也是可以为m的。
2. { x 1 , x 2 , x 3 . . . x k } \{x_1,x_2,x_3...x_k\} {x1​,x2​,x3​...xk​}，$x_i$最大也比$m$小，即不包含$m$，这样的拆分方式有$q(n,m-1)$。

这题纯递归会超时，考虑用数组存储递归生成的数据，防止数据重复生成（防止重复调用递归，递归优化版题解委托人写了，不要着急，会有的）

这里提供一下动态规划的写法

#include
int f[101][101];//记录[n][k]，拆分n，最大为k的拆分方法数
void divide(){
    for(int i=1;i<=100;i++)
        for(int j=1;j<=100;j++){
            if(i==1||j==1) f[i][j] = 1;
            else if(i==j) f[i][j]=f[i][j-1]+1;
            else if(i>j) f[i][j]=f[i][j-1]+f[i-j][j];
            else if(i<j) f[i][j]=f[i][i];
        }
}
int main(){
    int n,k;
    divide();//已经计算了[1~100][1~100]的拆分方法，后面直接读就行
    while(scanf("%d,%d",&n,&k)!=EOF){
        printf("%d\n",f[n][k]);
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

L2-3

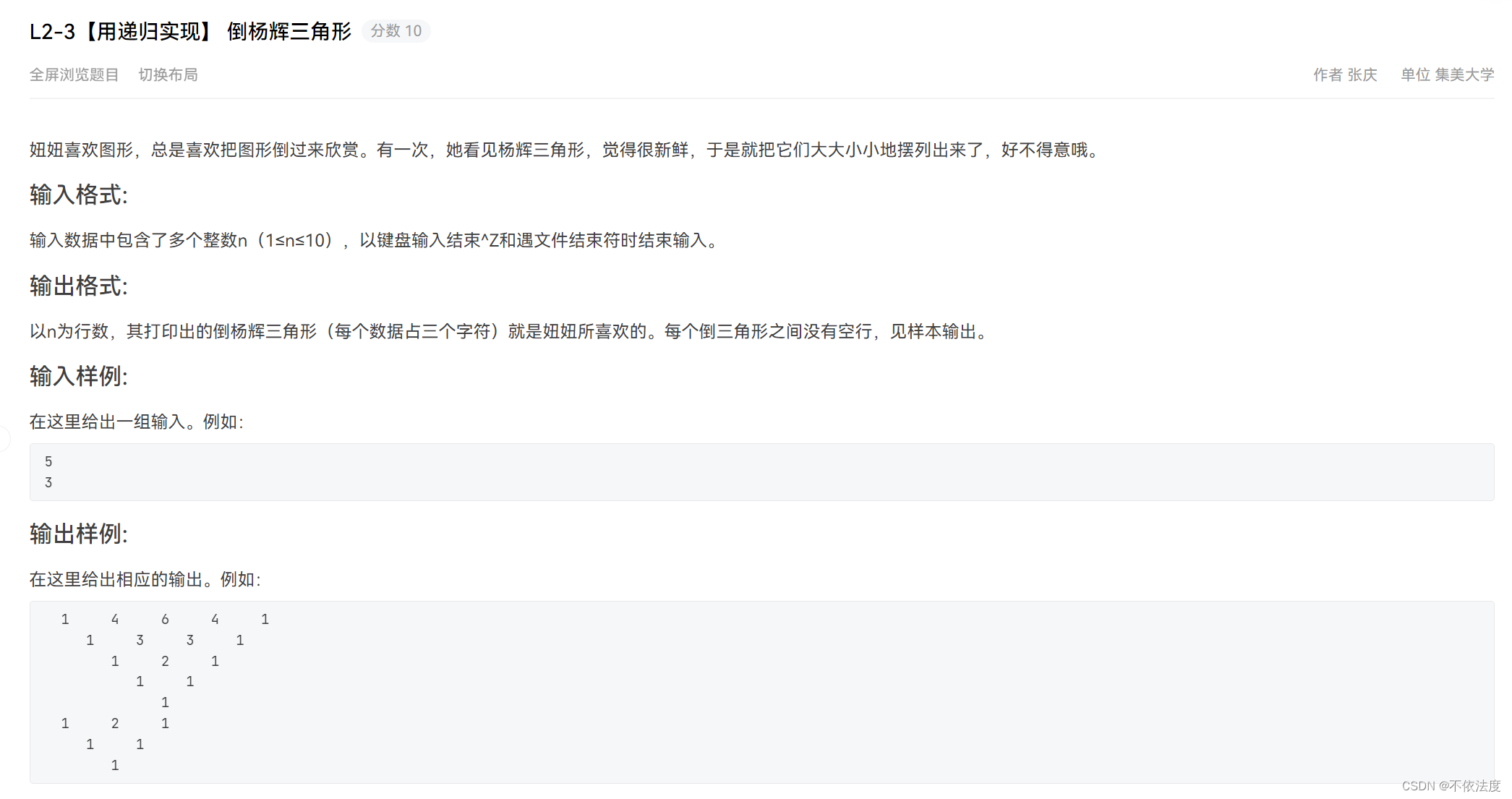
给个图提供一下思路，数组是这么存的，蓝色的是下标，红色的存储的数据，橙色的数据间的关系。

#include
int f[100][100];//初始都是0
void tangle(int x){
    for(int i = 1; i <= x; i++)
        for(int j = 1; j <= x; j++)
            if(!f[i][j]) f[i][j] = f[i][j-1] + f[i-1][j]; 
}
int main(){
    int k;
    for(int i=0; i<100; i++) f[i][0] = f[0][i] = 1;
    while(scanf("%d",&k)!=EOF){
        tangle(k);
        //处理输出格式
        for(int j = k-1; j >= 0; j--){
            for(int t = j; t < k-1; t++)
                printf("   ");
            for(int i = 0; i <= k-1&&j-i>=0; i++){
                if(i) printf("   ");
                printf("%3d",f[j-i][i]);   
               
            }
            printf("\n");
        }
       
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27