-
【无标题】
LSTM
通过引入遗忘门,输入门,输出门,缓解了RNN的梯度消失现象
三个门控制对前一段信息(主线遗忘)、输入信息(主线补给)以及输出信息的记忆状态,进而保证网络可以更好地学习到长距离依赖关系。
 遗忘门:通过判断当前输入的重要程度来决定对之前信息cell的保留度,遗忘多少历史信息
遗忘门:通过判断当前输入的重要程度来决定对之前信息cell的保留度,遗忘多少历史信息
F t = s i g m o i d ( W x f X + W h f H t − 1 ) F_t=sigmoid(W_{xf}X+W_{hf}H_{t-1}) Ft=sigmoid(WxfX+WhfHt−1)
输入门:通过判断当前输入的重要程度来决定对输入信息的保留度,补给多少当前信息
I t = s i g m o i d ( W x i X + W h i H t − 1 ) I_t=sigmoid(W_{xi}X+W_{hi}H_{t-1}) It=sigmoid(WxiX+WhiHt−1)
输出门:通过判断当前输入的重要程度来决定输出有多少来自记忆细胞
O t = s i g m o i d ( W x o X + W h o H t − 1 ) O_t=sigmoid(W_{xo}X+W_{ho}H_{t-1}) Ot=sigmoid(WxoX+WhoHt−1)
候选细胞单元: t a n h ( W x c X + W h c H t − 1 ) tanh(W_{xc}X+W_{hc}H_{t-1}) tanh(WxcX+WhcHt−1)
C t = F t C t − 1 + I t C ~ t C_t=F_tC_{t-1}+I_t \widetilde{C}_t Ct=FtCt−1+ItC t
H t = O t t a n h ( C t ) H_t =O_ttanh(C_t) Ht=Ottanh(Ct)GRU
GRU是对LSTM模型的优化,只有重置门和更新门,相比于LSTM,减少了很多参数,而且保证了效果
H ~ t = t a n h ( W h h X + W h h R t 点乘 H t − 1 ) \widetilde{H}_t=tanh(W_{hh}X+W_{hh}R_t点乘H_{t-1}) H t=tanh(WhhX+WhhRt点乘Ht−1)
H t = Z t H t − 1 + ( 1 − Z t H t ~ ) H_t=Z_tH_{t-1}+(1-Z_{t}\widetilde{H_t}) Ht=ZtHt−1+(1−ZtHt )LSTM和GRU的区别
GRU直接将隐藏状态信息传到下一时刻,LSTM将细胞状态包装成隐藏状态传入到下一时刻。
激活函数相关
1.sigmoid
优点:平滑处处可导
缺点:输出不是0均值(均大于0),输入的饱和区导数很小(容易导致梯度消失现象),存在幂运算,计算复杂
2.tanh
优点:平滑处处可导,输出是0均值
缺点:和sigmoid基本一样
3.ReLU
优点:计算速度快,大于0导数均为1,不容易发生梯度消失,收敛速度快
缺点:存在神经元永久死亡问题,输出不是0均值softmax
激活函数的一种,多分类
softmax之后得到每个类别的概率,然后计算交叉熵损失函数
交叉熵能表示预测分布和真实分布的差异,交叉体现在yi代表真实概率分布,pi代表预测概率分布,交叉熵越小,表示两个分布越接近。
H ( x ) = ∑ y i l o g ( p i ) H(x)=\sum y_ilog(p_i) H(x)=∑yilog(pi)优化器相关
不断通过调整参数去拟合数据
 对于优化算法,我们的目标是通过求每个参数的梯度来最小化损失函数,通过上面的代码我们可以发现,每个batch都需要计算一个损失函数,这与全量数据的损失函数肯定不一样,由于全量数据计算量大,我们用batch的损失函数代替整个训练集的损失函数。
对于优化算法,我们的目标是通过求每个参数的梯度来最小化损失函数,通过上面的代码我们可以发现,每个batch都需要计算一个损失函数,这与全量数据的损失函数肯定不一样,由于全量数据计算量大,我们用batch的损失函数代替整个训练集的损失函数。
为什么在鞍点会来回震荡?
因为我们每次计算的都是一个batch的loss图像,这带有一定的随机性,当换成下一个batch的时候,loss图像有不同,数据不一样,梯度肯定也不一样,如果是全量数据集,优化会停止不动。BGD 用整个训练集的样本计算去更新每个参数
好处:如果函数是凸函数,能收敛到全局最小值,非凸函数,收敛到局部最小值
计算量大,适用于小数据集
SGD随机挑选样本计算更新参数
mini-bactch GD用batch内的样本计算更新参数非凸函数:
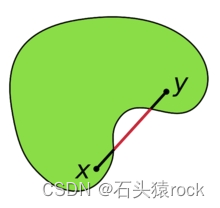

-
相关阅读:
华为数字化转型与数据管理实践介绍(附PPT下载)
记录我常用的linux(centOS)命令
Git——分布式版本控制工具
Unix Network Programming Episode 76
“低代码”编程或将是软件开发的未来
前端token知识梳理:token如何存储?token过期如何处理?如何无感刷新token?
Pads格式的PCB转换成Allegro操作指导
季节性壁炉布置:让您的家温馨如冬季仙境
umask 设置文件权限掩码
RK主机 CPU、NPU使用频率查看和设置
- 原文地址:https://blog.csdn.net/weixin_42887772/article/details/127434643