基于motoharw平台的电机控制策略模型simulink仿真实现

目录

一、理论基础

二、核心程序

三、仿真测试结果

---

一、理论基础

        HCU的控制算法开发是一个极其复杂的过程。其过程包括多个步骤：功能概念定义、算法开发、软件编程、底层操作系统和驱动程序开发、匹配标定及验证、ECU软件灌装等。这些步骤在多数情况下相互关联且反复循环。MotoTron公司的基于产品级ECU的控制策略快速开发平台（包括：MotoHawk算法开发软件，MotoTune刷写及标定软件，产品级ECU硬件）配合ATI公司的VISION标定工具，可为客户提供一套完整的解决方案。

       MotoHawk - Production ECU-based Rapid Prototyping

        MotoHawk是基于MotoTron的ControlCore产品级软件架构和产品级ECU硬件下的策略开发软件，开发人员在Matlab/Simulink/Stateflow/RTW 编译环境下编写基于体系结构的应用软件，其可应用在ECU开发、标定及测试的各个阶段。MotoHawk利用产品级ECU硬件平台，集成了车上常用的传感器接口和执行器驱动，大大缩短了从开发到产品化的周期，降低成本。   

        基于Motoharwa平台的电机控制策略模型是一个复杂而又精细的系统，它涉及到了电力电子技术、控制理论、电机学等多个学科领域。该平台使用了一种名为“单元控制策略”的方法来管理电机的运行，这种方法将电机控制看做是由一系列小型、互相独立的控制单元组成，每个单元负责各自的任务，并与其他单元协同工作以实现电机的整体控制。

一、控制原理

       电机控制策略的核心是“控制律”，它根据电机的运行状态，如转速、电流、电压等，以及设定的目标状态，如转矩、速度等，计算出需要的控制信号以驱动电机。在Motoharwa平台中，控制律由一系列数学公式组成，这些公式基于系统的物理模型和一些控制理论。

对于一个直流电机，其基本控制原理可以表示为：

T = KT_a * i + KT_b * n

       其中T是电机的输出转矩，i是电机的电流，n是电机的转速，KT_a和KT_b分别是电机转矩常数和控制常数。这个公式表示的是，电机的输出转矩由两部分组成：电流产生的转矩（KT_a * i）和控制信号产生的转矩（KT_b * n）。

二、数学模型

       在Motoharwa平台中，电机的数学模型是由一系列微分方程和差分方程组成的。这些方程描述了电机内部的各种物理过程，如电压、电流、电阻、电感等。通过这些模型，可以计算出电机的实时状态并预测其未来的行为。

例如，一个简单的直流电机模型可以表示为以下微分方程：

dT/dt = KT_a * i + KT_b * n - T/tau

       其中tau是电机的机械时间常数。这个方程描述的是电机的输出转矩随时间的变化率等于电流产生的转矩、控制信号产生的转矩减去电机的阻尼转矩。

三、控制流程

        在Motoharwa平台中，电机控制流程首先通过传感器采集电机的实时状态，如电流、电压、转速等。然后，这些状态被输入到控制单元中，控制单元使用这些信息以及设定的目标状态来计算出需要的控制信号。最后，这个控制信号被用于驱动电机，改变其运行状态以达到设定的目标。

        此外，Motoharwa平台还引入了一种名为“模型预测控制（MPC）”的先进控制算法。该算法使用预测模型来预测电机的未来行为，并使用优化算法来计算出最优的控制信号。这种算法能够处理复杂的动态系统，并优化系统的整体性能。

        总的来说，Motoharwa平台的电机控制策略模型是一种复杂而又精细的系统，它综合了电力电子技术、控制理论、电机学等多个学科领域的知识，并使用先进的控制算法来优化电机的整体性能。

二、核心程序

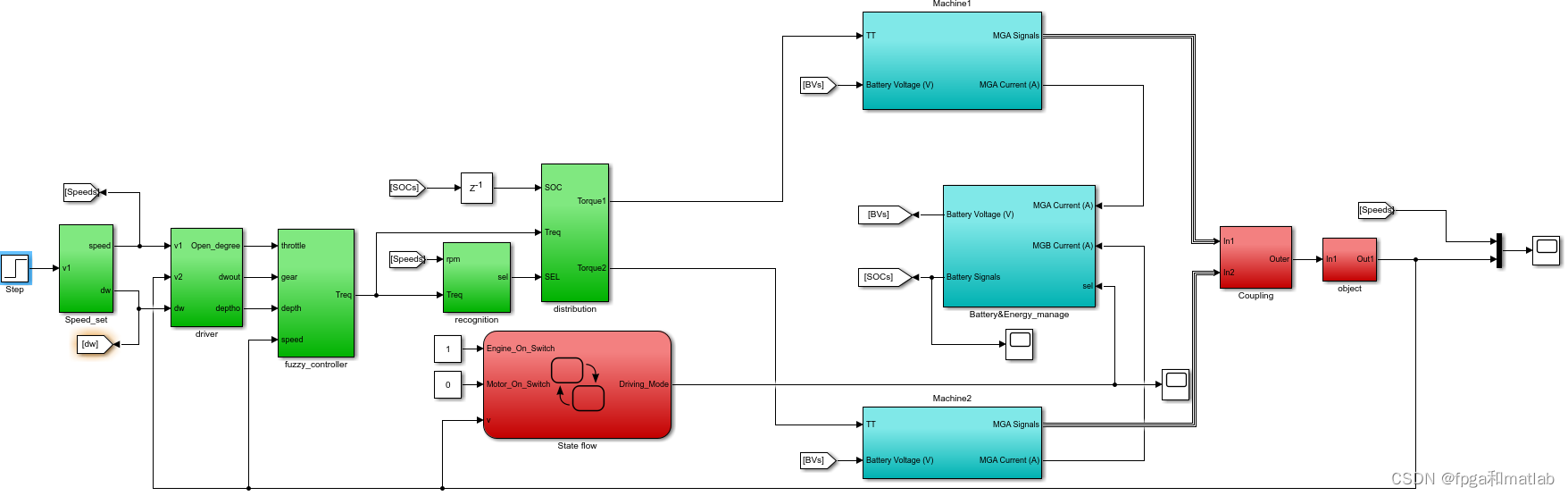
这个是基于原来那个模型，做了部分简化，然后增加了一个stateflow控制模块，其内部的状态转移结构如下所示：

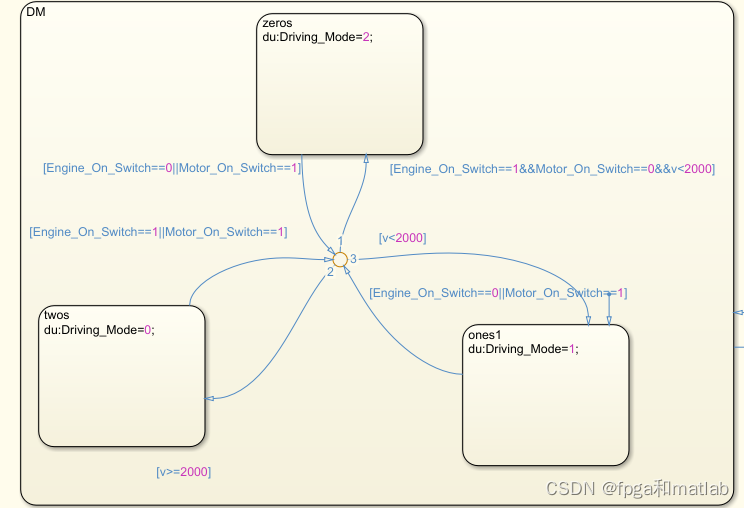
速度大于2000为状态0，速度小于2000位状态1，如果没有外部输入激励，状态2.

clc;
clear;
close all;
warning off;
 
%加载数据
load train_data.mat
 
data1    = a(:,2);
data2    = a(:,3);
E        = data1 - data2;
Ec       = diff(E);
E        = E(1:length(Ec));
pstudy1  = E;
pstudy2  = Ec;
trnData1 = pstudy1;
trnData2 = pstudy2;
trnData  = [trnData1,trnData2,data1(1:length(Ec))];
 
%由训练数据直接生成模糊推理系统
numMFs = 7;%隶属度函数个数
mfType = 'gbellmf';%类型
fisMat = genfis1(trnData,numMFs,mfType);
[x1,mf1] = plotmf(fisMat,'input',1);%初始隶属度函数
[x2,mf2] = plotmf(fisMat,'input',2);%初始隶属度函数
figure;
subplot(121);plot(x1,mf1);title('E-Initial membership functions');
subplot(122);plot(x2,mf2);title('Ec-Initial membership functions');
 
 
%使用进行给定数据的神经模糊建模
numEpochs=400;%训练次数
fisMat1=anfis(trnData,fisMat,numEpochs);
 
%训练后模糊推理系统的隶属函数曲线
[x1,mf1]=plotmf(fisMat1,'input',1);
[x2,mf2]=plotmf(fisMat1,'input',2);
figure;
subplot(121);plot(x1,mf1);title('E  - Fiual Membership Functions');
subplot(122);plot(x2,mf2);title('Ec - Fiual Membership Functions');
 
% save patient1.mat fisMat
save patient2.mat fisMat1
 
figure;
plot(data1(1:length(Ec)),'b');hold on
plot(evalfis([E,Ec],fisMat1),'r-o');hold off;

三、仿真测试结果

        为了测试方便，我这里做的简化，主要有如下几个方面：

第一、去掉了原来的模糊控制器，这样仿真速度可以快点，测试简单；

第二、将控制模型简化了，用一个传递函数来表示；

第三、增加了stateflow状态转移控制器。

        仿真结果如下所示：

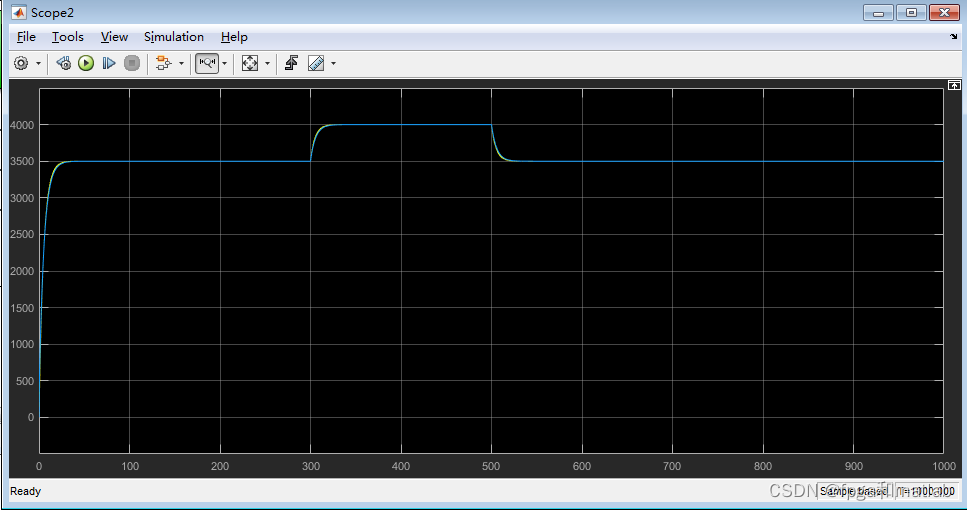
        基本上信号的输入输出都需要借助工具箱中的CANread和CANsend模块进行输入输出。因为这个涉及到硬件，所以你这边自己需要根据硬件设备对CANread和CANsend做简单的配置。

        然后我仔细看了下硬件设备的接口配置，所以我们需要预留如下接口，作为在环设计的输入和输出接口。

        再整个模型中，首先放如下如下的模块：

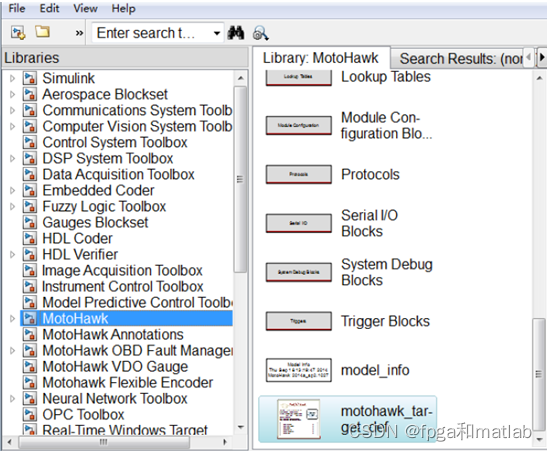
       另外,再设置下canread和canwrite就可以了。我提供的第一个文件夹的工程，就是用来给你熟悉设备使用的。

A22-15