码农知识堂 - 1000bd
  •   Python
  •   PHP
  •   JS/TS
  •   JAVA
  •   C/C++
  •   C#
  •   GO
  •   Kotlin
  •   Swift

  • 【3D视觉原理】3-3D数据表示与转换

    文章目录

    • 内容
    • 深度图和点云的数据存储
      • 体像素 - 空间均匀分割
        • 3D数据体像素存储 - 改进：存储
        • 3D数据体像素存储-代码示例
        • 从体像素数组转回点云数据
        • 体像素的应用
          • 1 快速检测空间点是否被占据
          • 2 体像素之间的逻辑运算，实现3D、 形状的组合和编辑
        • 体像素存储的优缺点
          • 运算速度快
          • 存储效率很低，尺寸分辨率和空间相互矛盾
      • 八叉树 - 空间非均匀按需分割
        • 2D数据 - 4叉树
          • 2D数据的4叉树表示
          • 2D数据的4叉树构建
          • 2D数据的4叉树构建 - 算法 改进
          • 4叉树应用 - 快速“碰撞”检测
          • 4叉树构建 - 代码示例
          • 4叉树搜索 - 代码示例
        • 3D数据 - 8叉树
          • 3D数据 - 8叉树 - 表示
          • 3D数据 - 8叉树 - 构建
          • 3D数据 - 8叉树 - 构建 - 改进
          • 3D数据 - 8叉树 - 应用
            • 快速“碰撞”检测
            • 3D光线追踪
            • knn搜索
          • 3D数据 - 8叉树 - 代码示例 - Python
            • 3D数据 - 8叉树 - 构建 - 代码示例 - Python
            • 3D数据 - 8叉树 - 查询 - 代码示例 - Python
          • 3D数据 - 8叉树 - 代码示例 - PCL（C++实现，效率高）
      • Kd树（k-dimensional tree）
        • 从4叉树到kd树
        • KD树 - 应用 - 实现快速最近邻查找
        • KD树 - 构建
          • 如何选择分割平面的方向？
          • KD树 - 构建 - 2D - 示例
          • KD树 - 构建 - 3D - 代码示例
        • KD树 - 搜索 - 最近邻
        • KD树 - 搜索 - k近邻 - Python
        • KD树 - 搜索 - k近邻 - PCL（C++实现，效率更高）
      • 三角剖分
        • 三角剖分 - 应用 - 人脸3D模型
        • 如何将随机点划分为三角形？ - Delaunay 三角剖分
        • Delaunay 三角剖分
          • Delaunay 三角剖分 - 局部优化（Local Optimization Procedure，LOP）
          • Delaunay 三角剖分 - 全局优化算法Bowyer-Watson
          • Delaunay 三角剖分 - 代码实现 - Python
          • Delaunay 三角剖分 - 问题
            • 2D平面上的三角剖分用于3D曲面
            • 空间任意曲面的三角剖分
            • 深度图上的简易三角剖分
    • PLY数据文件格式
      • 基本格式内容
        • 头部内容
        • 数据部分
        • PLY数据格式 - 彩色 - 示例
    • 作业

    内容

    深度图和点云的数据存储（体像素、八叉树、Kd树、三角剖分）
    PLY数据文件格式

    深度图和点云的数据存储

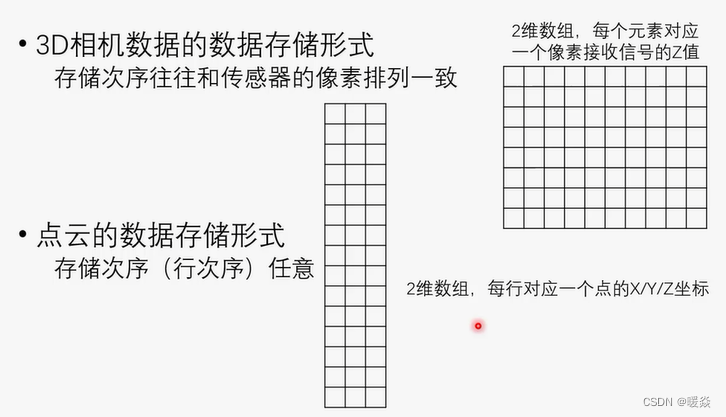
    在这里插入图片描述

    3D相机数据的数据存储形式是二维数组，元素值为物体距离像平面距离Z或者视线距离d。

    点云数据存储形式是二维数组，但只有三列 ( X , Y , Z ) (X,Y,Z) (X,Y,Z)，行存储次序任意。

    体像素 - 空间均匀分割

    在这里插入图片描述

    3D数据体像素存储 - 改进：存储

    在这里插入图片描述

    3D数据体像素存储-代码示例

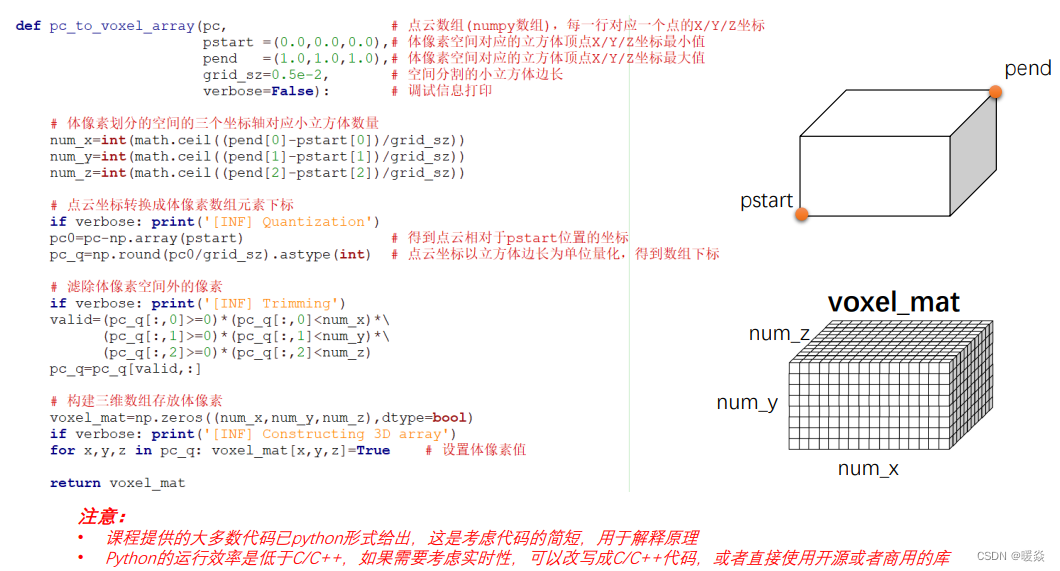
    在这里插入图片描述
    在这里插入图片描述

    从体像素数组转回点云数据

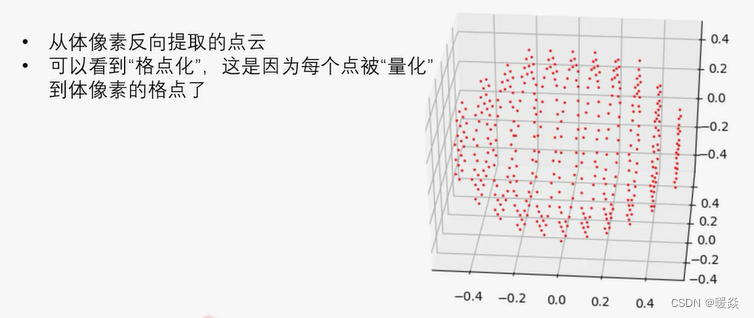
    在这里插入图片描述

    体像素的应用

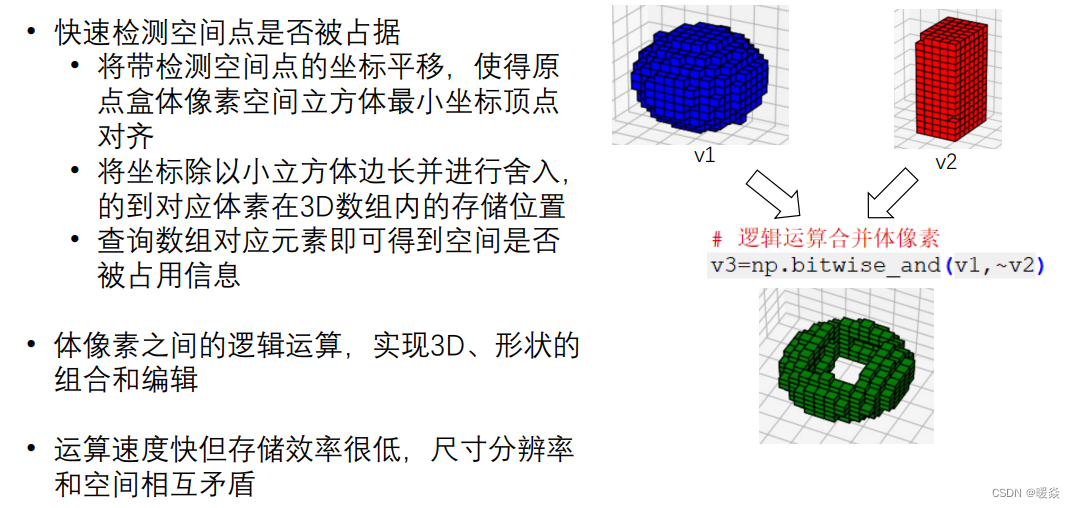
    在这里插入图片描述

    1 快速检测空间点是否被占据

    将带检测空间点的坐标平移，使得原点盒体像素空间立方体最小坐标顶点对齐。

    将坐标除以小立方体边长并进行舍入，得到对应体素在3D数组内的存储位置。

    查询数组对应元素即可得到空间是否被占用信息。

    2 体像素之间的逻辑运算，实现3D、 形状的组合和编辑

    体像素存储的优缺点

    运算速度快
    存储效率很低，尺寸分辨率和空间相互矛盾

    需要很大的空间存储3D数组。

    量化的精度越高，划分的体像素的格子越多，存储空间越大。

    八叉树 - 空间非均匀按需分割

    体像素一使 用空间的均匀分割
    八叉树一 对空间非均匀分割(按需分割)
    具体讨论8叉树之前，我们先从4叉树说起
    ●2D数据的4叉树表示
    ●3D数据的8叉树表示

    2D数据 - 4叉树

    2D数据的4叉树表示

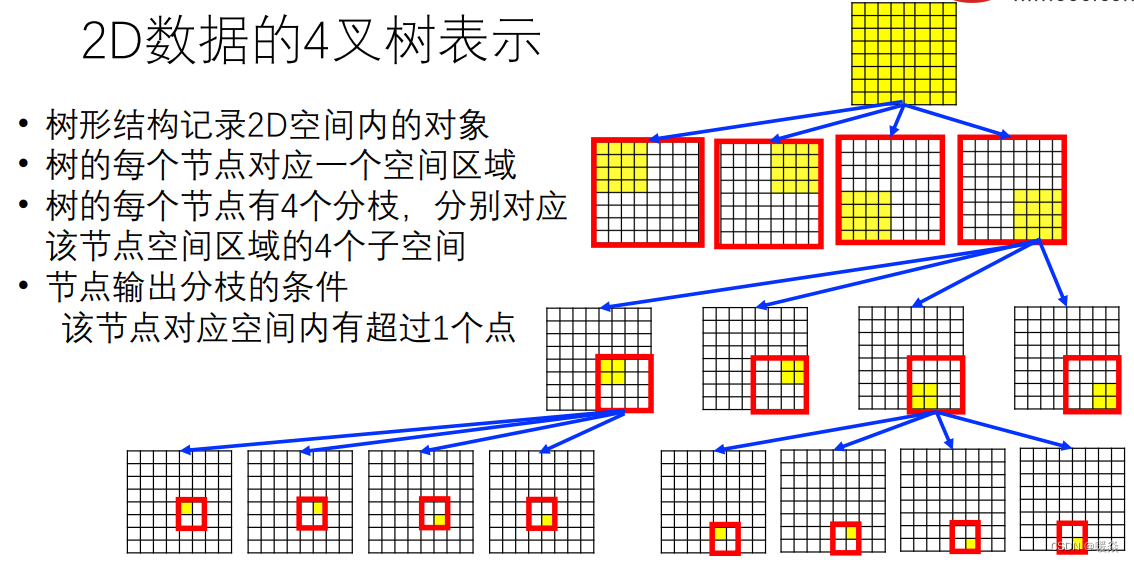
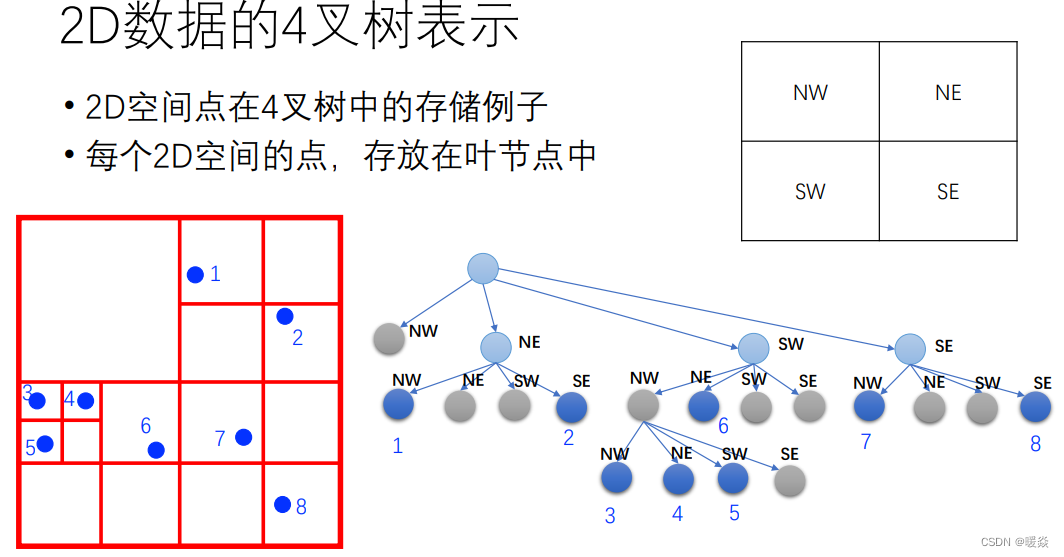
    在这里插入图片描述
    在这里插入图片描述

    2D数据的4叉树构建

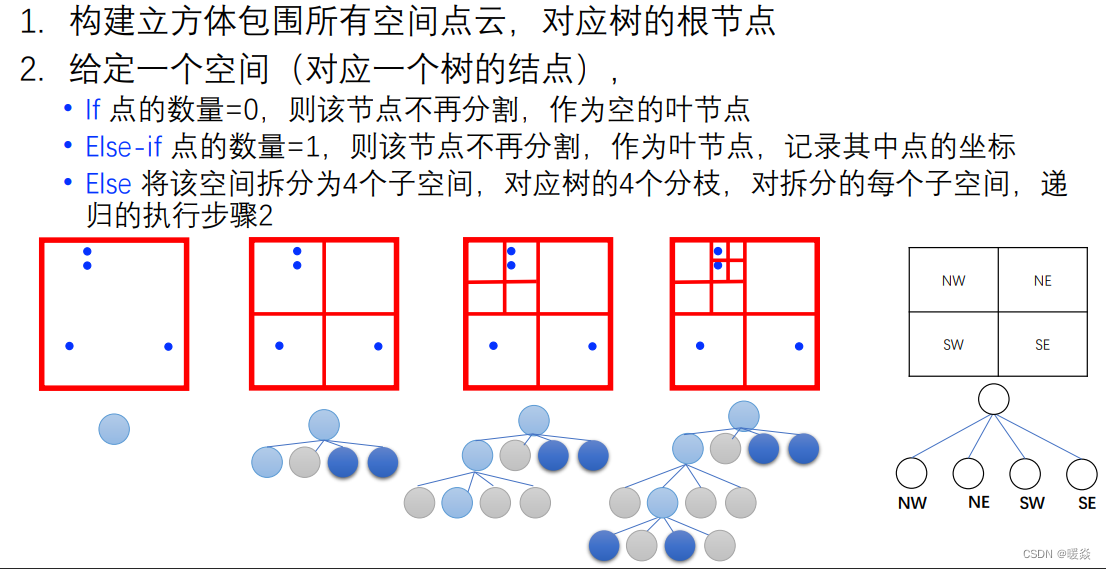
    在这里插入图片描述

    2D数据的4叉树构建 - 算法 改进

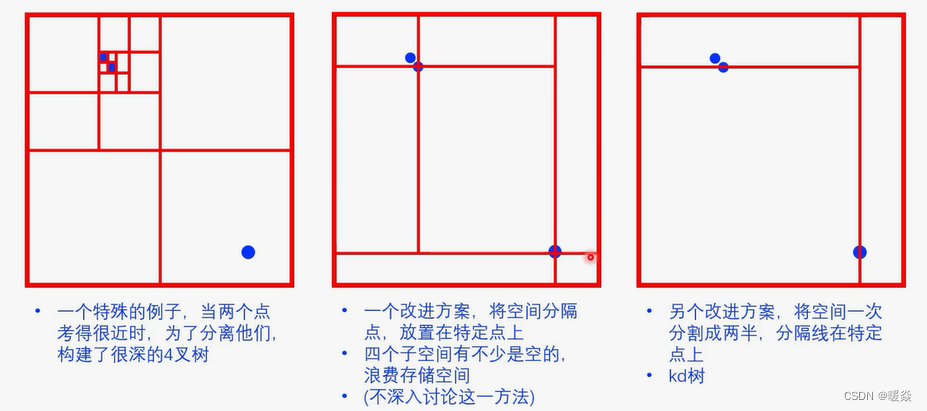
    如下图所示的情况，如果使用上面的方法构建4叉树，树会很深，浪费空间。针对这种情况，提出三种改进方式。

    在这里插入图片描述

    4叉树应用 - 快速“碰撞”检测

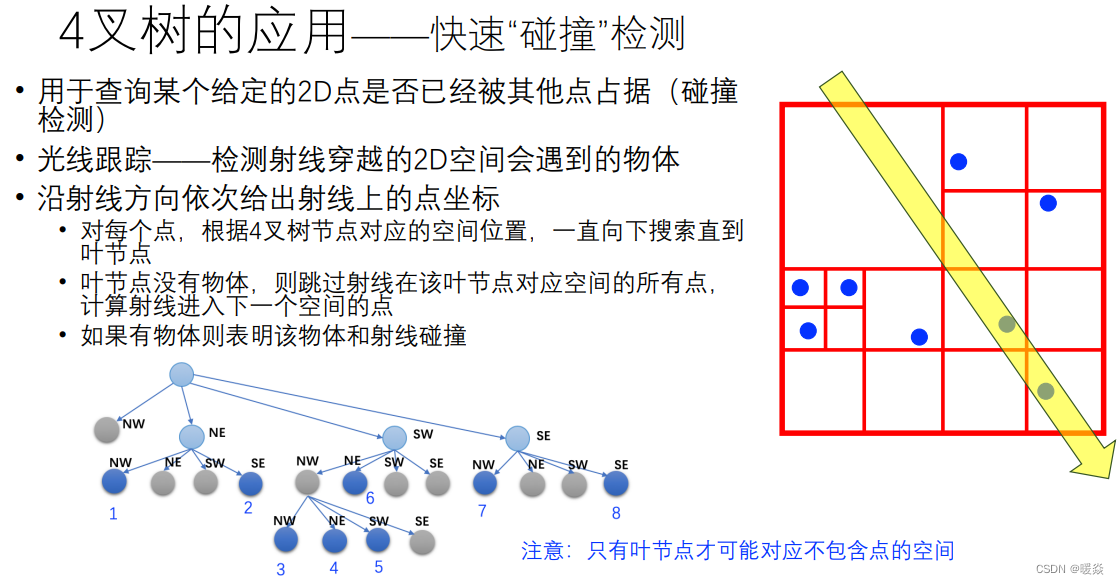
    在这里插入图片描述

    4叉树构建 - 代码示例

    在这里插入图片描述

    4叉树搜索 - 代码示例

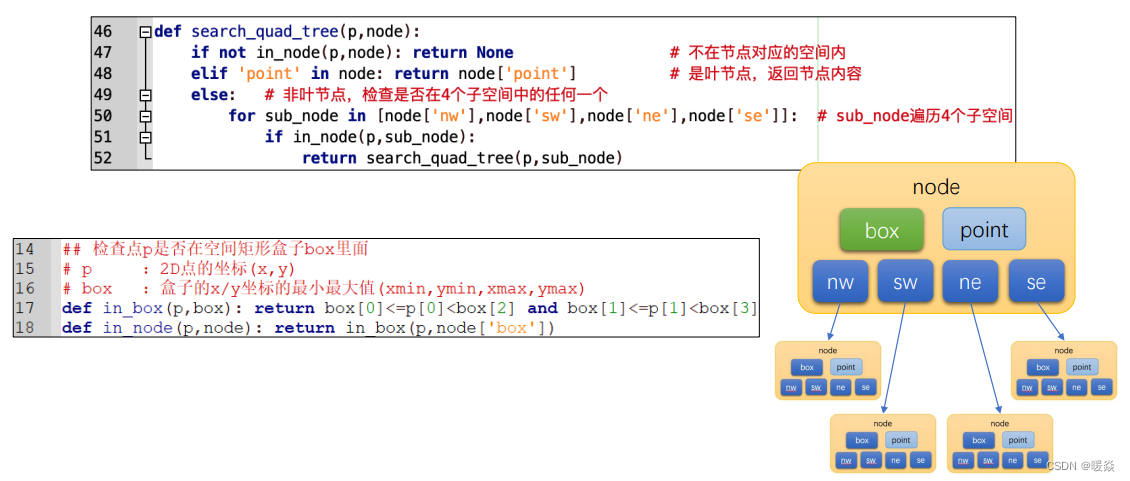
    在这里插入图片描述

    3D数据 - 8叉树

    3D数据 - 8叉树 - 表示

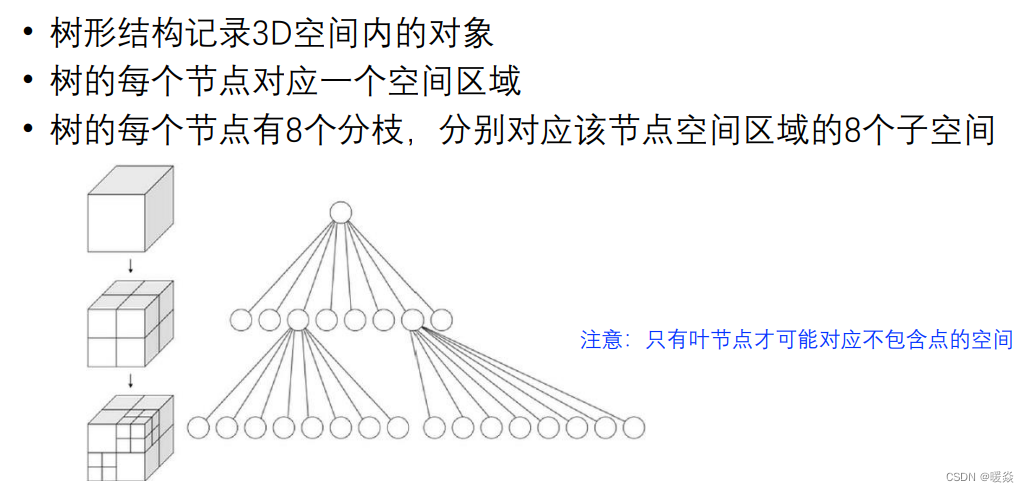
    在这里插入图片描述

    3D数据 - 8叉树 - 构建

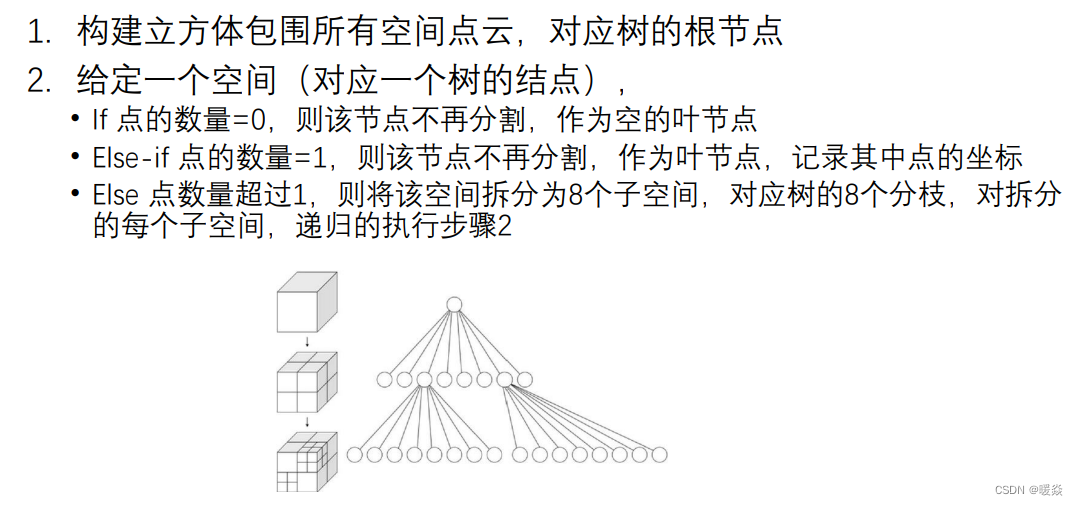
    在这里插入图片描述

    3D数据 - 8叉树 - 构建 - 改进

    1 拆分的停止条件可以改成空间内点的数量小于给定正整数K。

    2 拆分的停止条件可以改成节点对应空间立方体边长小于门限。

    3 叶节点存放的多个点的坐标数据。

    3D数据 - 8叉树 - 应用
    快速“碰撞”检测
    3D光线追踪
    knn搜索

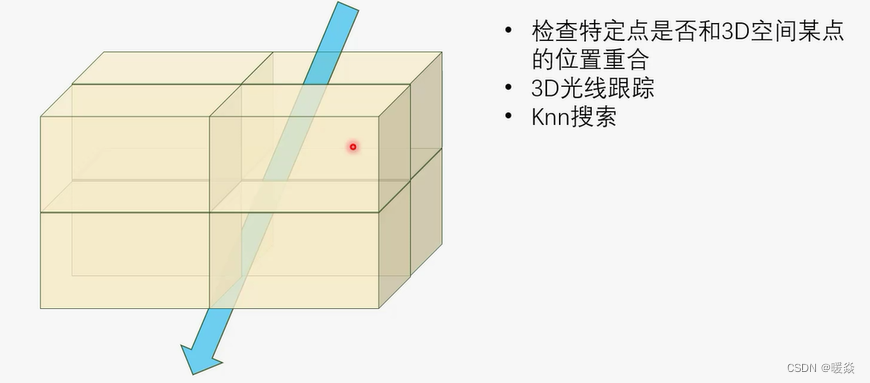
    在这里插入图片描述

    3D数据 - 8叉树 - 代码示例 - Python
    3D数据 - 8叉树 - 构建 - 代码示例 - Python

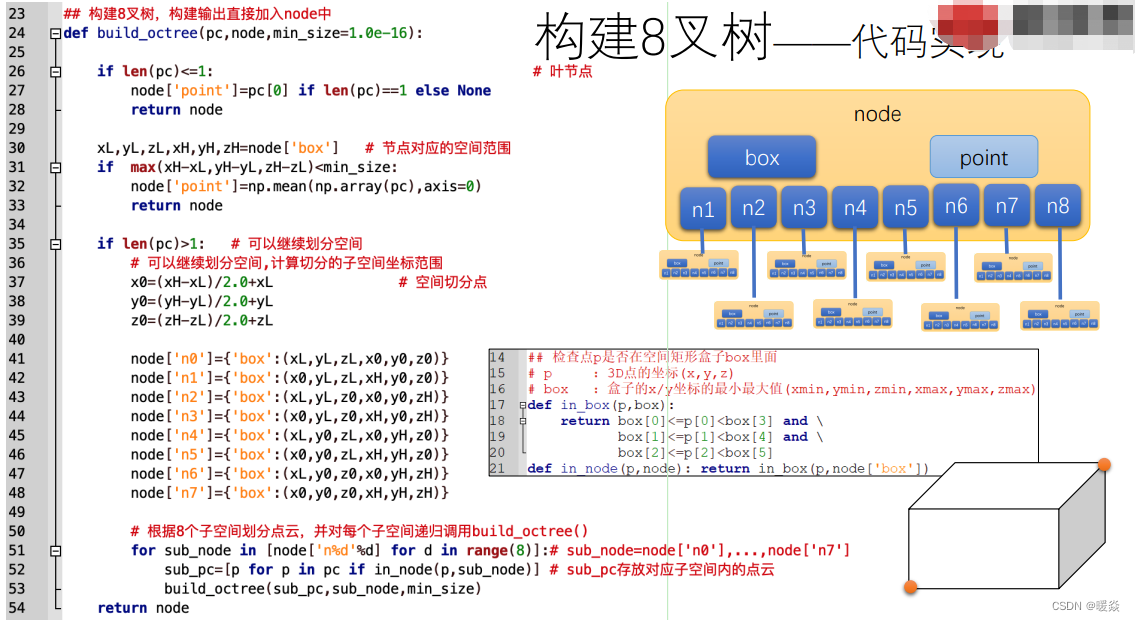
    在这里插入图片描述

    3D数据 - 8叉树 - 查询 - 代码示例 - Python

    在这里插入图片描述

    3D数据 - 8叉树 - 代码示例 - PCL（C++实现，效率高）

    在这里插入图片描述

    Kd树（k-dimensional tree）

    从4叉树到kd树

    在这里插入图片描述

    KD树 - 应用 - 实现快速最近邻查找

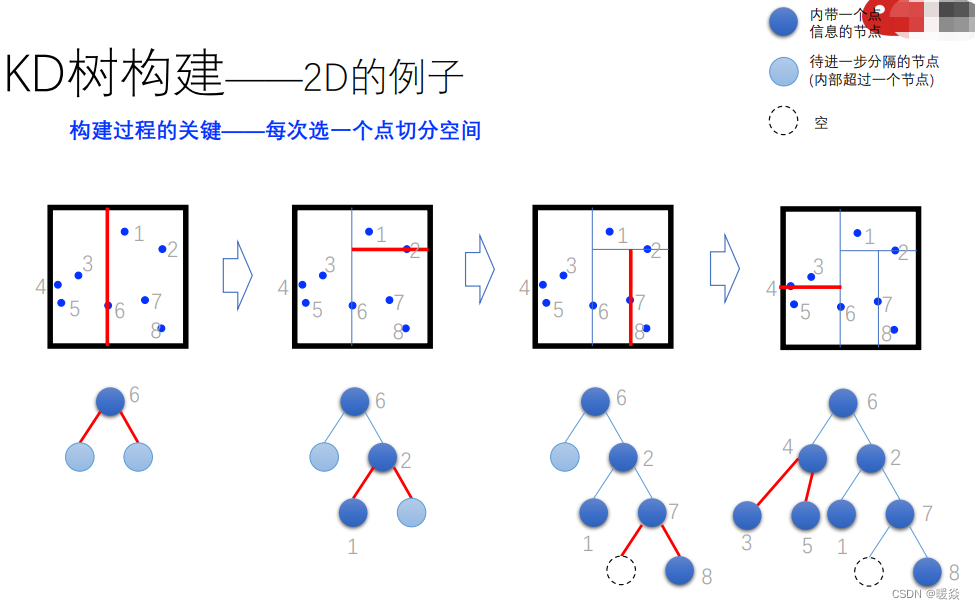
    KD树 - 构建

    在这里插入图片描述

    如何选择分割平面的方向？

    分割平面有三个方向可以选择：垂直于x轴，垂直于y轴，垂直于z轴。

    树的不同层使用不同的方向，例如：树第一层使用垂直于x轴分割，树第二层使用垂直于y轴分割。

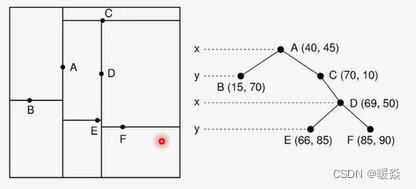
    KD树 - 构建 - 2D - 示例

    在这里插入图片描述
    在这里插入图片描述

    KD树 - 构建 - 3D - 代码示例

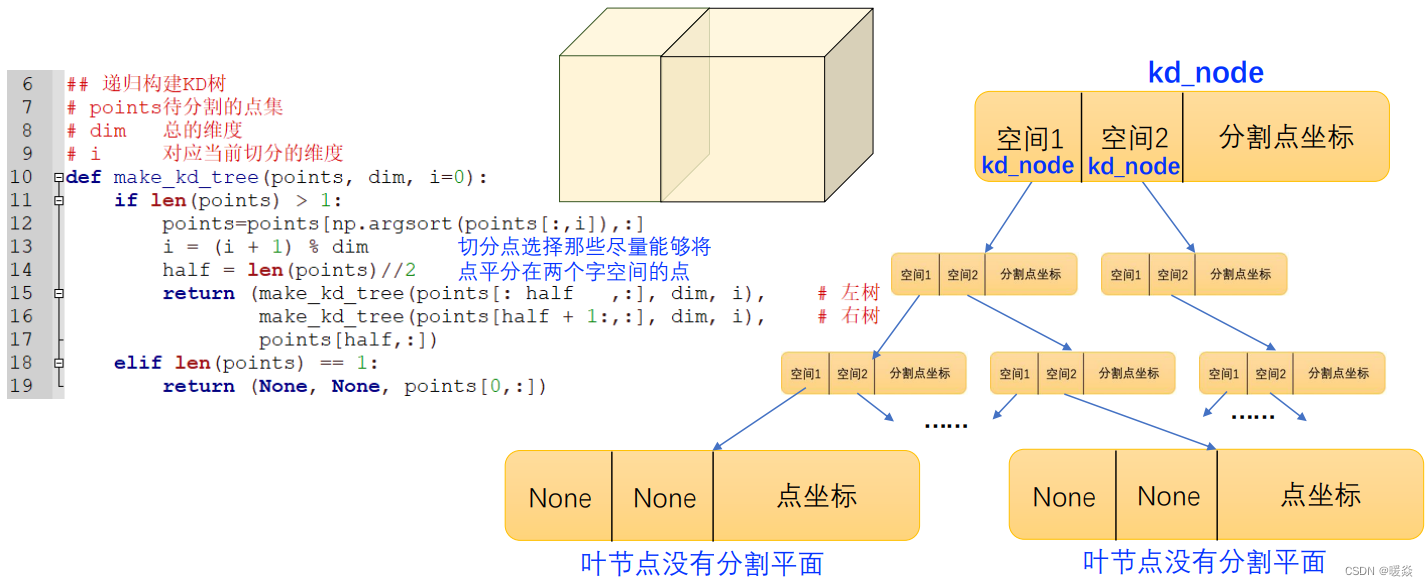
    在这里插入图片描述

    KD树 - 搜索 - 最近邻

    在这里插入图片描述
    在这里插入图片描述

    KD树 - 搜索 - k近邻 - Python

    k 近邻与最近邻搜索算法思想相同，只是 k 近邻搜索中，使用优先级队列保存k个近邻。

    在这里插入图片描述

    KD树 - 搜索 - k近邻 - PCL（C++实现，效率更高）

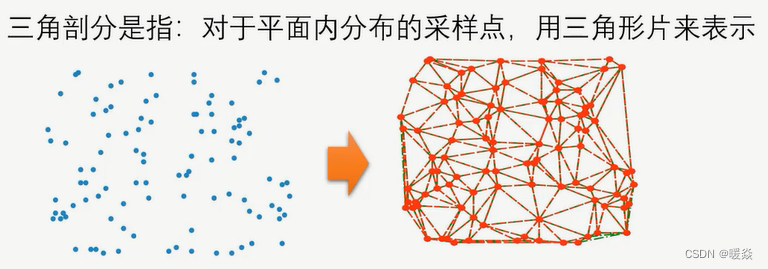
    在这里插入图片描述

    三角剖分

    在这里插入图片描述

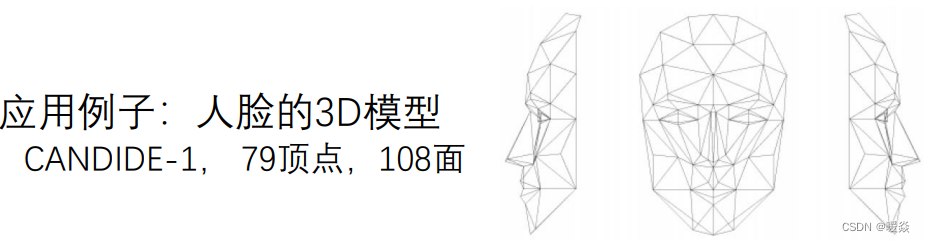
    三角剖分 - 应用 - 人脸3D模型

    在这里插入图片描述

    如何将随机点划分为三角形？ - Delaunay 三角剖分

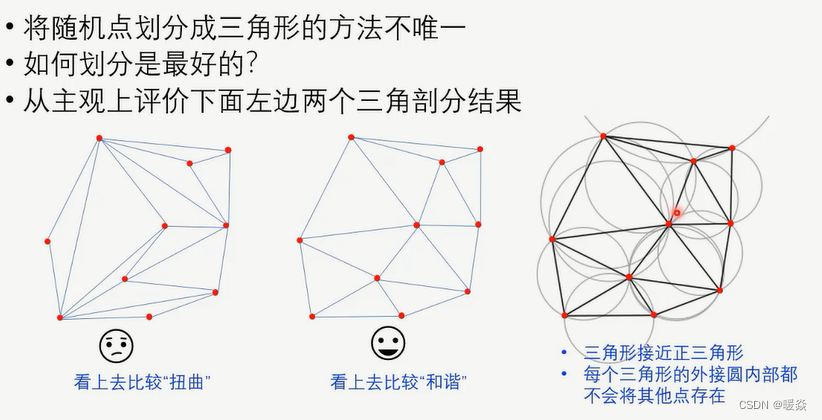
    在这里插入图片描述

    Delaunay 三角剖分

    准则：1 空圆；2 最大化最小角。

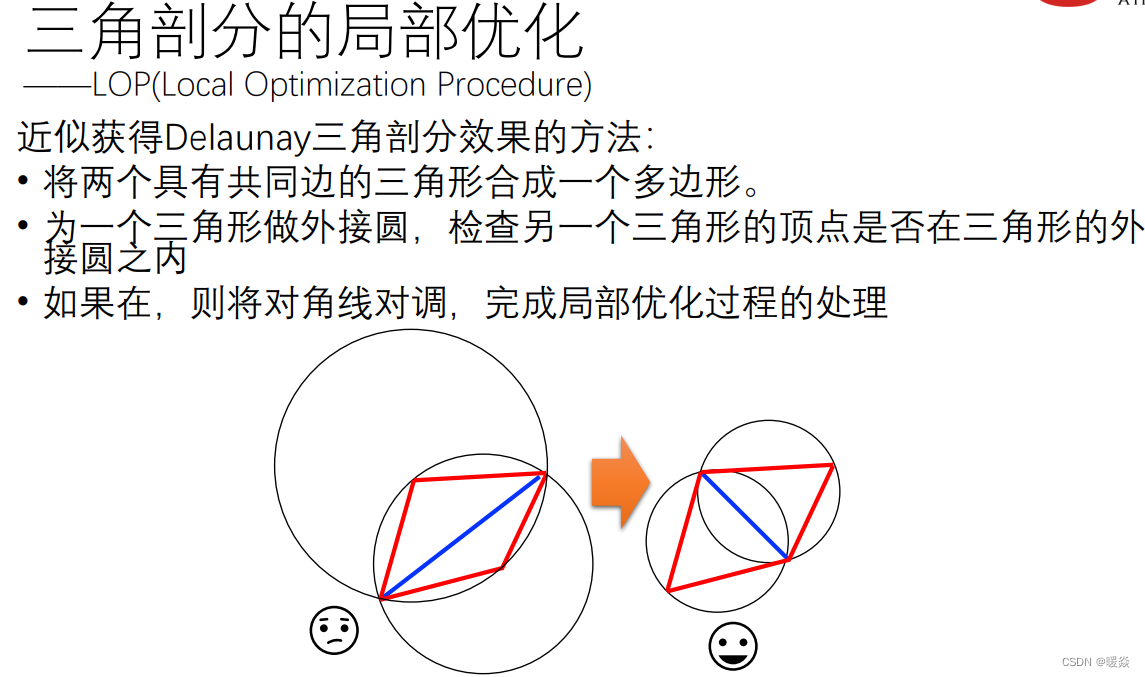
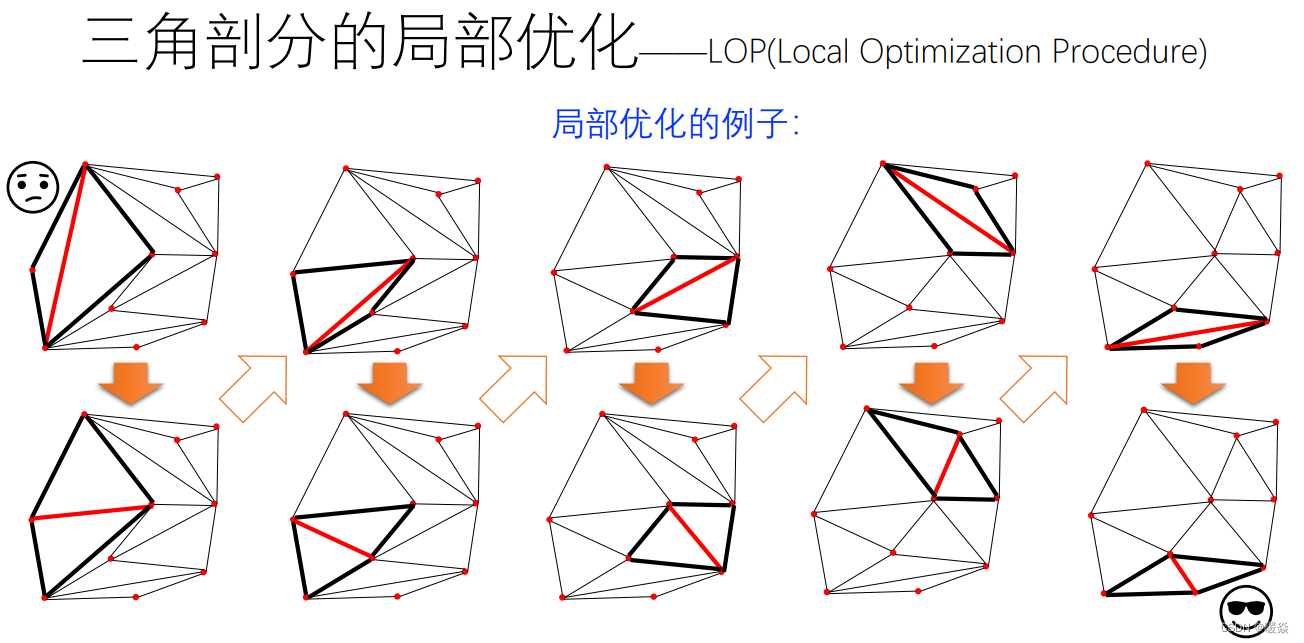
    在这里插入图片描述

    Delaunay 三角剖分 - 局部优化（Local Optimization Procedure，LOP）

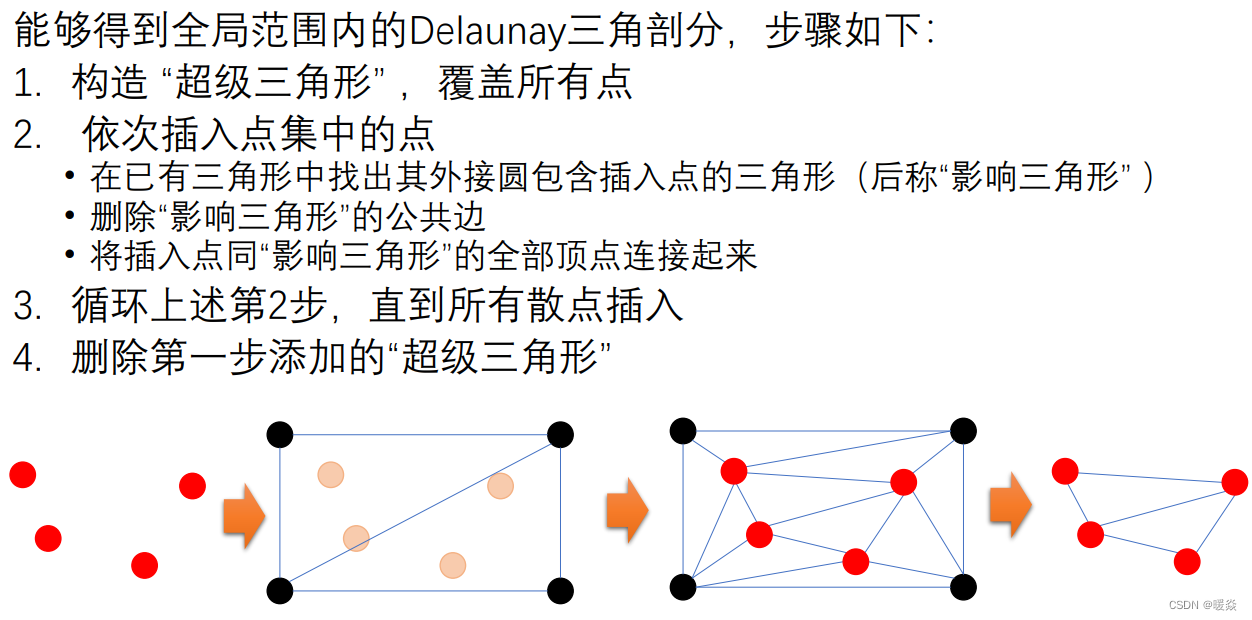
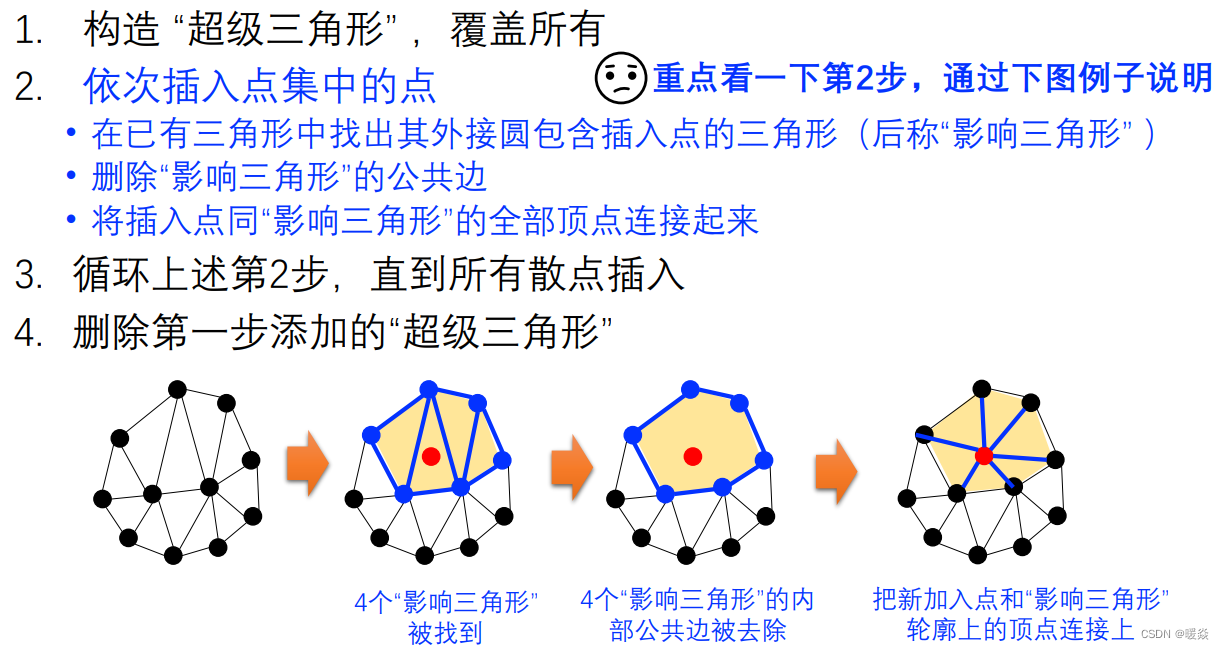
    在这里插入图片描述

    在这里插入图片描述

    Delaunay 三角剖分 - 全局优化算法Bowyer-Watson

    在这里插入图片描述

    在这里插入图片描述

    Delaunay 三角剖分 - 代码实现 - Python

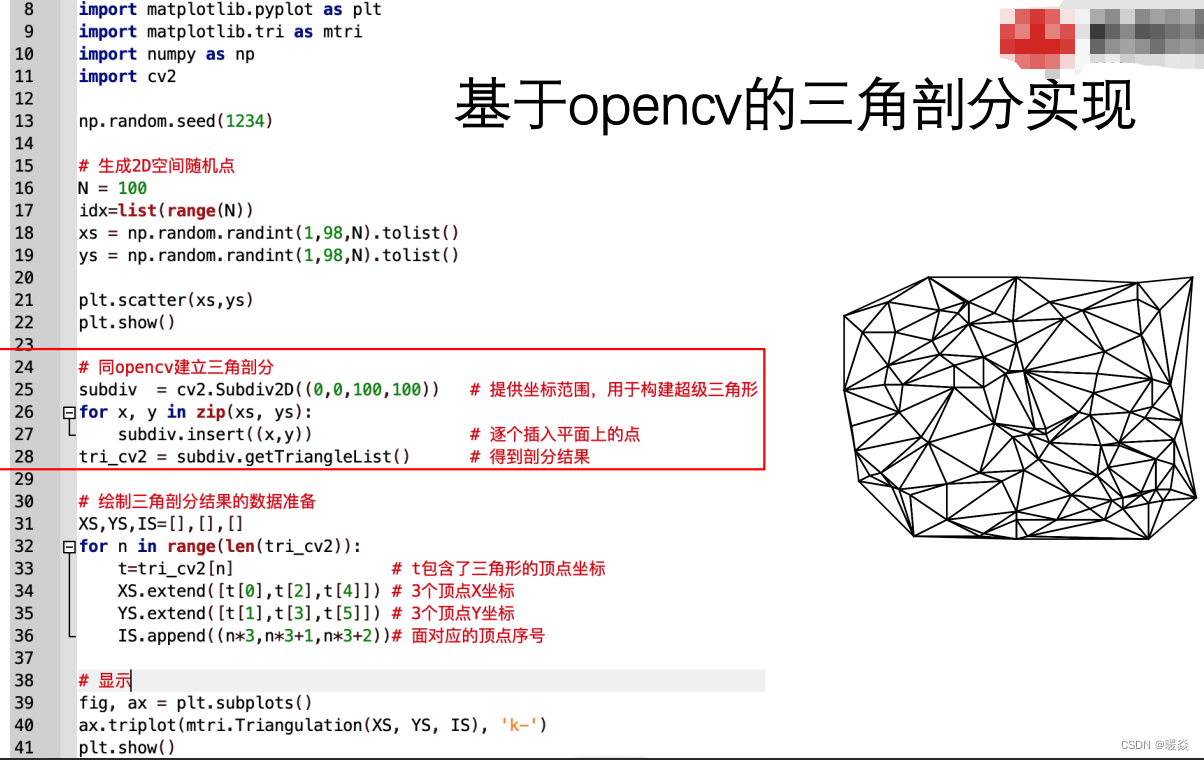
    在这里插入图片描述

    Delaunay 三角剖分 - 问题
    2D平面上的三角剖分用于3D曲面

    曲面的局部看成近似平面，将采样点投影到拟合平面上，进行三角划分。
    使用近似的方法，从任一局部小三角形出发，不断“蔓延”， 期间用LOP进行局部优化。

    空间任意曲面的三角剖分

    结合SDF函数的marching Cube算法。

    深度图上的简易三角剖分

    以深度图平面上的均匀采样格点直接做三角化。

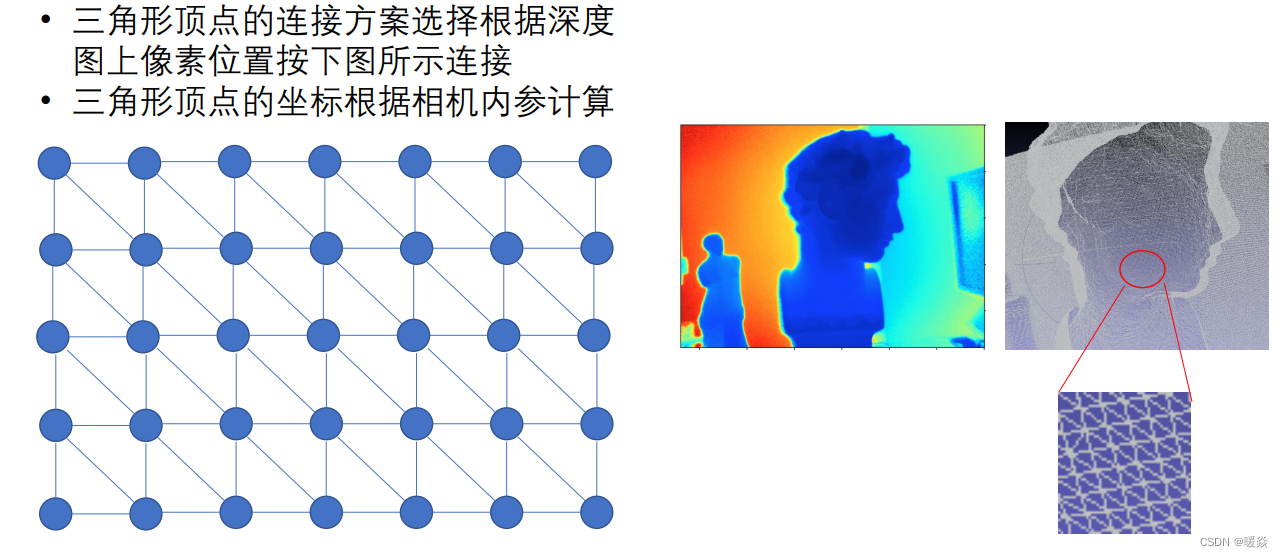
    在这里插入图片描述

    注：顶点间可以拼凑成“米”字形。

    PLY数据文件格式

    1 用多个平面片（三角形或者四边形）描述空间几何体表面

    2 有ASCII和二进制2种格式（这里只介绍ASCII格式）

    3 平面片描述拆分为:

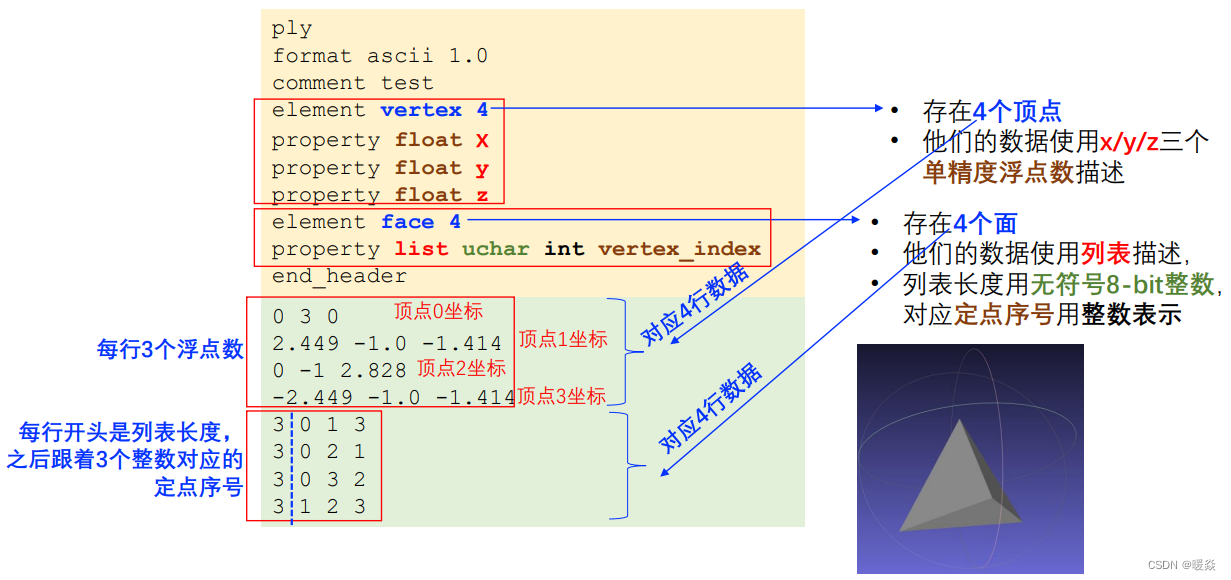
    1)顶点描述;
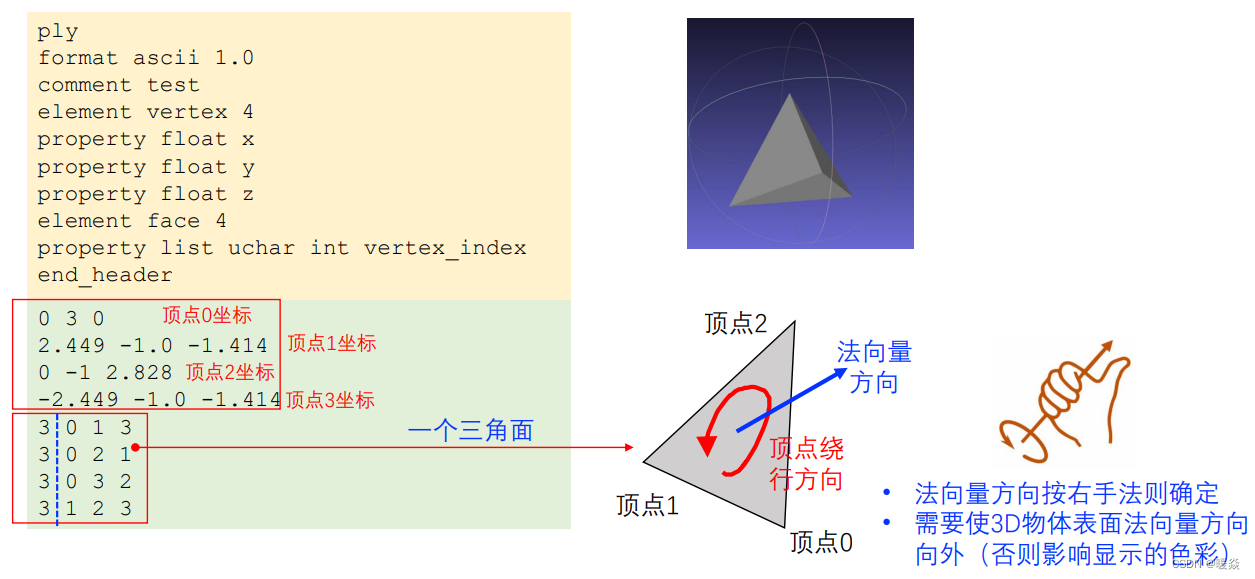
    2)构成平面片的顶点序号

    基本格式内容

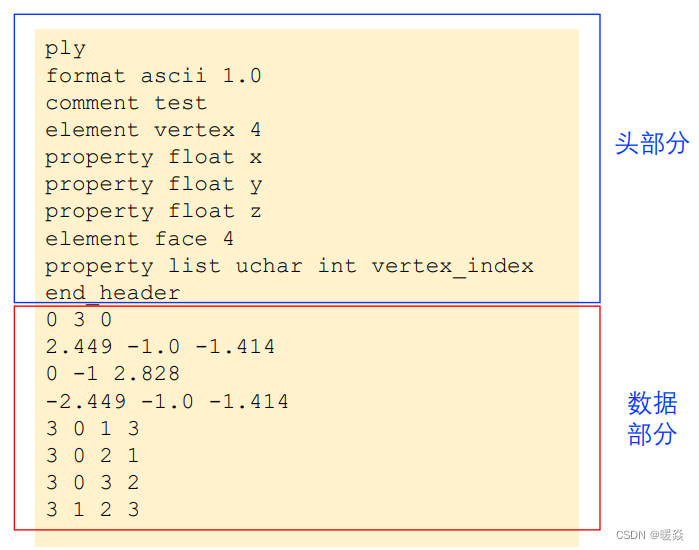
    在这里插入图片描述

    头部内容

    在这里插入图片描述

    数据部分

    在这里插入图片描述

    平面的法向量方向：右手法则。平面三个坐标点的顺序即为食指绕行方向。

    法向量方向会影响渲染出来3D平面的颜色。如果平面法向量朝内，渲染出的平面颜色不是彩色而是灰色。

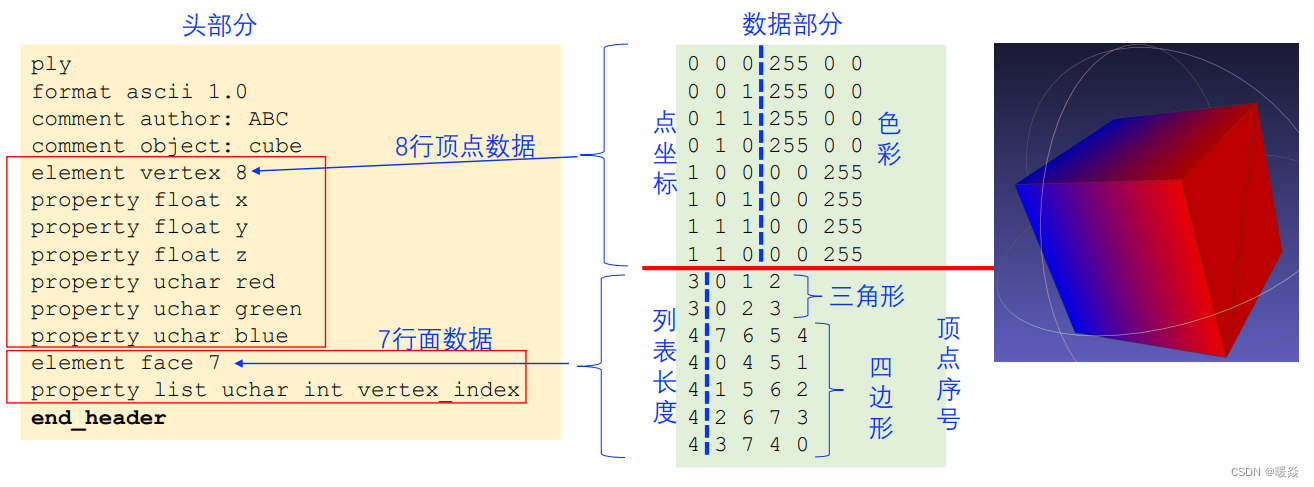
    在这里插入图片描述

    PLY数据格式 - 彩色 - 示例

    在这里插入图片描述

    作业

    在这里插入图片描述

    在这里插入图片描述

  • 相关阅读:
    C语言编程陷阱（八）
    滚珠花键各大品牌简述
    《游戏编程模式》学习笔记（十二）类型对象 Type Object
    查出来这个表中evaluation_num字段中以2023开头的最大的尾数是几，instr用法
    caffeine学习笔记
    sky walking日志采集以及注意事项
    React学习笔记（番外一）——video.js视频播放组件的入门及排坑经历
    【学习笔记】Java安全之动态加载字节码
    【Camera基础（一）】Camera摄像头工作原理及整机架构
    小程序转 App 帮助企业打开营销局面
  • 原文地址：https://blog.csdn.net/guai7guai11/article/details/127061135
  • 最新文章
  • 攻防演习之三天拿下官网站群
    数据安全治理学习——前期安全规划和安全管理体系建设
    企业安全 | 企业内一次钓鱼演练准备过程
    内网渗透测试 | Kerberos协议及其部分攻击手法
    0day的产生 | 不懂代码的"代码审计"
    安装scrcpy-client模块av模块异常，环境问题解决方案
    leetcode hot100【LeetCode 279. 完全平方数】java实现
    OpenWrt下安装Mosquitto
    AnatoMask论文汇总
    【AI日记】24.11.01 LangChain、openai api和github copilot
  • 热门文章
  • 十款代码表白小特效 一个比一个浪漫 赶紧收藏起来吧！！！
    奉劝各位学弟学妹们，该打造你的技术影响力了！
    五年了，我在 CSDN 的两个一百万。
    Java俄罗斯方块，老程序员花了一个周末，连接中学年代！
    面试官都震惊，你这网络基础可以啊！
    你真的会用百度吗？我不信 — 那些不为人知的搜索引擎语法
    心情不好的时候，用 Python 画棵樱花树送给自己吧
    通宵一晚做出来的一款类似CS的第一人称射击游戏Demo！原来做游戏也不是很难，连憨憨学妹都学会了！
    13 万字 C 语言从入门到精通保姆级教程2021 年版
    10行代码集2000张美女图，Python爬虫120例，再上征途
Copyright © 2022 侵权请联系2656653265@qq.com    京ICP备2022015340号-1
正则表达式工具 cron表达式工具 密码生成工具

京公网安备 11010502049817号